
Question and Answers Forum
Question Number 40130 by maxmathsup by imad last updated on 16/Jul/18
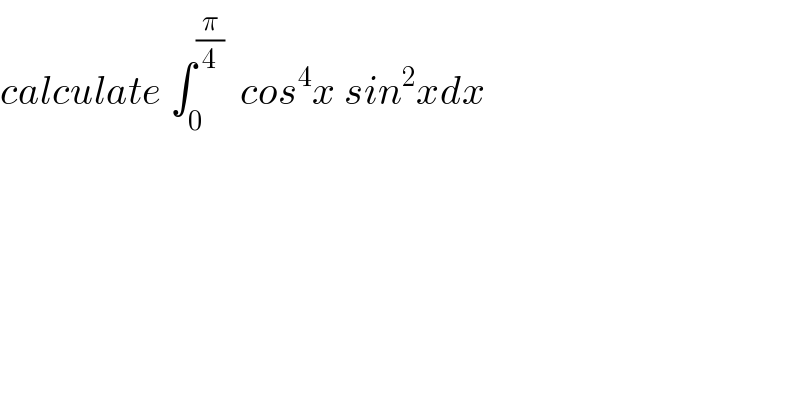
Commented by math khazana by abdo last updated on 21/Jul/18
![let I = ∫_0 ^(π/4) cos^4 x sin^2 xdx by parts I = ∫_0 ^(π/4) sinx cos^4 x sinx dx =[−(1/5) cos^5 x sinx]_0 ^(π/4) −∫_0 ^(π/4) (−(1/5))cos^5 x cosxdx =−(1/5)(((√2)/2))^6 +(1/5) ∫_0 ^(π/4) cos^6 x dx but ∫_0 ^(π/4) cos^6 xdx = ∫_0 ^(π/4) (((1+cos(2x))/2))^3 dx =(1/8) ∫_0 ^(π/4) { cos^3 (2x) +3cos^2 (2x) +3cos(2x)+1)}dx =(1/8) ∫_0 ^(π/4) cos^3 (2x)dx +(3/8) ∫_0 ^(π/4) ((1+cos(4x))/2)dx +(3/8) ∫_0 ^(π/4) cos(2x)dx +(π/(32)) but ∫_0 ^(π/4) cos(2x)dx=[(1/2)sin(2x)]_0 ^(π/4) =(1/2) ∫_0 ^(π/4) ((1+cos(4x))/2)dx =(π/8) +(1/8)[sin(4x)]_0 ^(π/4) =(π/8) ∫_0 ^(π/4) cos^3 (2x)dx = ∫_0 ^(π/4) cos(2x)((1+cos(4x))/2)dx =(1/2) ∫_0 ^(π/4) cos(2x) +(1/2) ∫_0 ^(π/4) cos(2x)cos(4x)dx =(1/4)[sin(2x)]_0 ^(π/4) +(1/4) ∫_0 ^(π/4) {cos(6x)+cos(2x))dx =(1/4) +(1/(24))[sin(6x)]_0 ^(π/4) +(1/8)[sin(2x)]_0 ^(π/4) =(1/4) −(1/(24)) +(1/8) =((6−1+3)/(24)) =(8/(24)) =(1/3) so the value of I is determined.](Q40437.png)
| ||
Question and Answers Forum | ||
Question Number 40130 by maxmathsup by imad last updated on 16/Jul/18 | ||
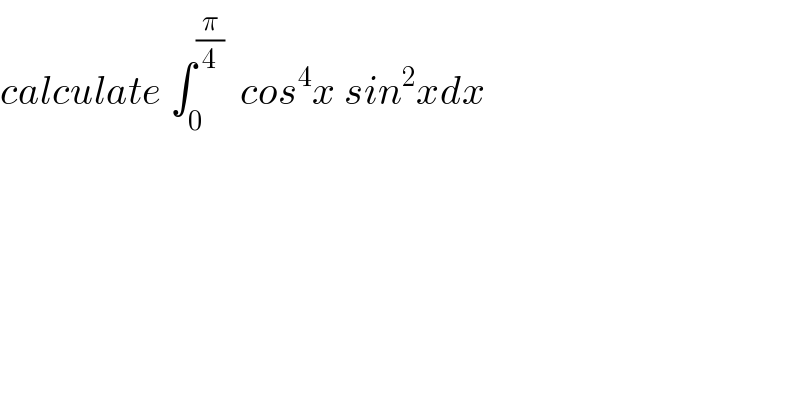 | ||
Commented by math khazana by abdo last updated on 21/Jul/18 | ||
![let I = ∫_0 ^(π/4) cos^4 x sin^2 xdx by parts I = ∫_0 ^(π/4) sinx cos^4 x sinx dx =[−(1/5) cos^5 x sinx]_0 ^(π/4) −∫_0 ^(π/4) (−(1/5))cos^5 x cosxdx =−(1/5)(((√2)/2))^6 +(1/5) ∫_0 ^(π/4) cos^6 x dx but ∫_0 ^(π/4) cos^6 xdx = ∫_0 ^(π/4) (((1+cos(2x))/2))^3 dx =(1/8) ∫_0 ^(π/4) { cos^3 (2x) +3cos^2 (2x) +3cos(2x)+1)}dx =(1/8) ∫_0 ^(π/4) cos^3 (2x)dx +(3/8) ∫_0 ^(π/4) ((1+cos(4x))/2)dx +(3/8) ∫_0 ^(π/4) cos(2x)dx +(π/(32)) but ∫_0 ^(π/4) cos(2x)dx=[(1/2)sin(2x)]_0 ^(π/4) =(1/2) ∫_0 ^(π/4) ((1+cos(4x))/2)dx =(π/8) +(1/8)[sin(4x)]_0 ^(π/4) =(π/8) ∫_0 ^(π/4) cos^3 (2x)dx = ∫_0 ^(π/4) cos(2x)((1+cos(4x))/2)dx =(1/2) ∫_0 ^(π/4) cos(2x) +(1/2) ∫_0 ^(π/4) cos(2x)cos(4x)dx =(1/4)[sin(2x)]_0 ^(π/4) +(1/4) ∫_0 ^(π/4) {cos(6x)+cos(2x))dx =(1/4) +(1/(24))[sin(6x)]_0 ^(π/4) +(1/8)[sin(2x)]_0 ^(π/4) =(1/4) −(1/(24)) +(1/8) =((6−1+3)/(24)) =(8/(24)) =(1/3) so the value of I is determined.](Q40437.png) | ||