
Question and Answers Forum
Question Number 32353 by abdo imad last updated on 23/Mar/18
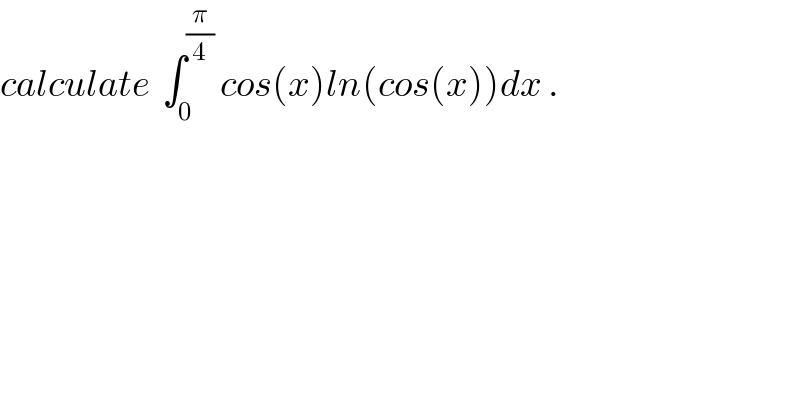
Answered by sma3l2996 last updated on 25/Mar/18
![A=∫_0 ^(π/4) cos(x)ln(cosx)dx by parts u=ln(cosx)⇒u′=−tanx v′=cosx⇒v=sinx A=[sin(x)ln(cosx)]_0 ^(π/4) +∫_0 ^(π/4) ((sin^2 x)/(cosx))dx=−((√2)/4)ln(2)+∫_0 ^(π/4) ((1/(cosx))−cosx)dx let t=tan(x/2) A=−((√2)/4)ln(2)−[sinx]_0 ^(π/4) +∫_0 ^(tan(π/8)) (dt/(1−t^2 )) =−((√2)/4)ln(2)−((√2)/2)+(1/2)[ln∣((1+t)/(1−t))∣]_0 ^(tan(π/8)) A=−((√2)/4)ln(2)−((√2)/2)+(1/2)ln((2/(1−tan(π/8)))−1)](Q32465.png)
| ||
Question and Answers Forum | ||
Question Number 32353 by abdo imad last updated on 23/Mar/18 | ||
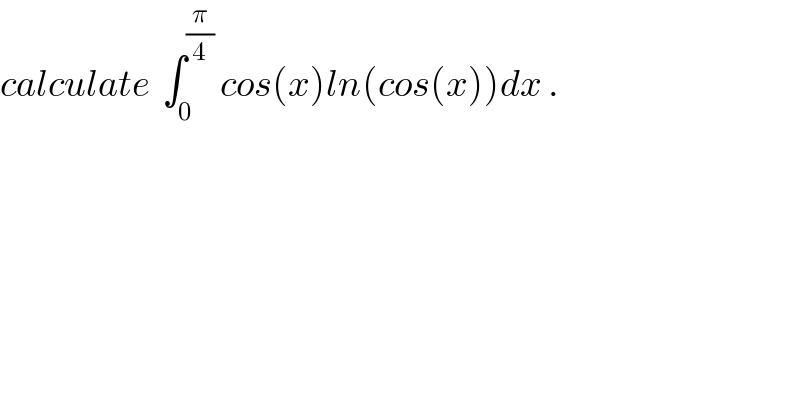 | ||
Answered by sma3l2996 last updated on 25/Mar/18 | ||
![A=∫_0 ^(π/4) cos(x)ln(cosx)dx by parts u=ln(cosx)⇒u′=−tanx v′=cosx⇒v=sinx A=[sin(x)ln(cosx)]_0 ^(π/4) +∫_0 ^(π/4) ((sin^2 x)/(cosx))dx=−((√2)/4)ln(2)+∫_0 ^(π/4) ((1/(cosx))−cosx)dx let t=tan(x/2) A=−((√2)/4)ln(2)−[sinx]_0 ^(π/4) +∫_0 ^(tan(π/8)) (dt/(1−t^2 )) =−((√2)/4)ln(2)−((√2)/2)+(1/2)[ln∣((1+t)/(1−t))∣]_0 ^(tan(π/8)) A=−((√2)/4)ln(2)−((√2)/2)+(1/2)ln((2/(1−tan(π/8)))−1)](Q32465.png) | ||
| ||