
Question and Answers Forum
Question Number 35685 by prof Abdo imad last updated on 22/May/18
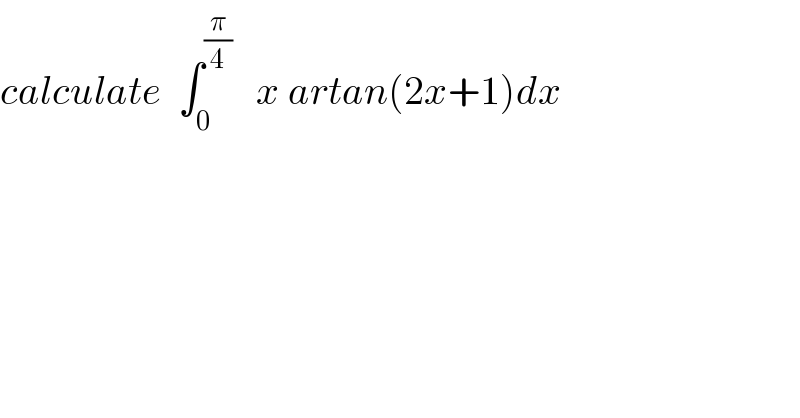
Commented by prof Abdo imad last updated on 23/May/18
![let put I = ∫_0 ^(π/4) x arctan(2x+1)dx by parts I = [ (x^2 /2)arctan(2x+1)]_0 ^(π/4) − ∫_0 ^(π/4) (x^2 /2) (2/(1 +(2x+1)^2 ))dx =(π^2 /(32))arctan((π/2)+1) −∫_0 ^(π/4) (x^2 /(1+(2x+1)^2 ))dx let calculate J= ∫_0 ^(π/4) (x^2 /(1+(2x+1)^2 ))dx J =_(2x+1=u) ∫_1 ^((π/2)+1) (((((u−1)/2))^2 )/(1+u^2 )) (du/2) = (1/8) ∫_1 ^((π/2)+1) ((u^2 −2u +1)/(1+u^2 ))du 8J = ∫_1 ^((π/2)+1) (1 −((2u)/(1+u^2 )))du = (π/2) −[ ln(1+u^2 )]_1 ^((π/2)+1) =(π/2) −{ ln(1+((π/2)+1)^2 ) −ln(2)} ⇒ J = (π/(16)) −(1/8){ln(1+((π/2)+1)^2 ) −ln(2)} so I = (π^2 /(32)) arctan((π/2)+1) −(π/(16)) +(1/8){ln(1+((π/2)+1)^2 )−ln(2)}](Q35795.png)
Answered by ajfour last updated on 23/May/18
![I=(x^2 /2)tan^(−1) (2x+1)∣_0 ^(π/4) −∫_0 ^( π/4) ((x^2 /2))[(2/(1+(2x+1)^2 ))]dx =(π^2 /(32))tan^(−1) (1+(π/2))−I_1 I_1 =(1/4)∫_0 ^( π/4) ((1+(2x+1)^2 −2(2x+1))/(1+(2x+1)^2 ))dx =(x/4)∣_0 ^(π/4) −(1/4)∫_( 2) ^( 1+(1+(π/2))^2 ) (dt/t) =(π/(16))−(1/4)ln [(1/2)+(((π+2)^2 )/8)] I = (π^2 /(32))tan^(−1) (1+(π/2))−(π/(16)) +(1/4)ln [(1/2)+(((π+2)^2 )/8)] .](Q35803.png)
| ||
Question and Answers Forum | ||
Question Number 35685 by prof Abdo imad last updated on 22/May/18 | ||
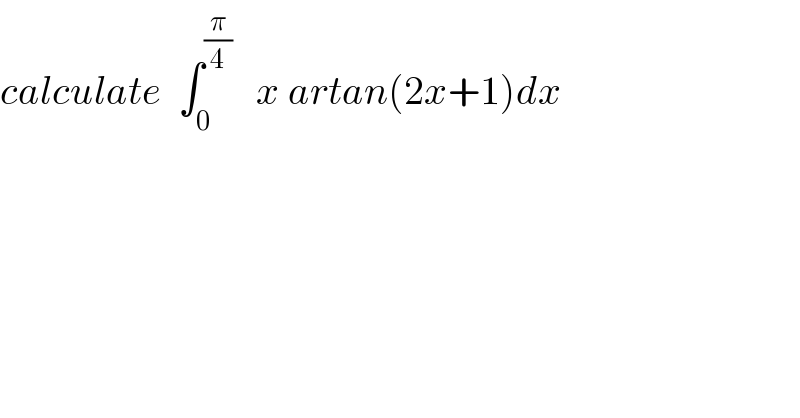 | ||
Commented by prof Abdo imad last updated on 23/May/18 | ||
![let put I = ∫_0 ^(π/4) x arctan(2x+1)dx by parts I = [ (x^2 /2)arctan(2x+1)]_0 ^(π/4) − ∫_0 ^(π/4) (x^2 /2) (2/(1 +(2x+1)^2 ))dx =(π^2 /(32))arctan((π/2)+1) −∫_0 ^(π/4) (x^2 /(1+(2x+1)^2 ))dx let calculate J= ∫_0 ^(π/4) (x^2 /(1+(2x+1)^2 ))dx J =_(2x+1=u) ∫_1 ^((π/2)+1) (((((u−1)/2))^2 )/(1+u^2 )) (du/2) = (1/8) ∫_1 ^((π/2)+1) ((u^2 −2u +1)/(1+u^2 ))du 8J = ∫_1 ^((π/2)+1) (1 −((2u)/(1+u^2 )))du = (π/2) −[ ln(1+u^2 )]_1 ^((π/2)+1) =(π/2) −{ ln(1+((π/2)+1)^2 ) −ln(2)} ⇒ J = (π/(16)) −(1/8){ln(1+((π/2)+1)^2 ) −ln(2)} so I = (π^2 /(32)) arctan((π/2)+1) −(π/(16)) +(1/8){ln(1+((π/2)+1)^2 )−ln(2)}](Q35795.png) | ||
Answered by ajfour last updated on 23/May/18 | ||
![I=(x^2 /2)tan^(−1) (2x+1)∣_0 ^(π/4) −∫_0 ^( π/4) ((x^2 /2))[(2/(1+(2x+1)^2 ))]dx =(π^2 /(32))tan^(−1) (1+(π/2))−I_1 I_1 =(1/4)∫_0 ^( π/4) ((1+(2x+1)^2 −2(2x+1))/(1+(2x+1)^2 ))dx =(x/4)∣_0 ^(π/4) −(1/4)∫_( 2) ^( 1+(1+(π/2))^2 ) (dt/t) =(π/(16))−(1/4)ln [(1/2)+(((π+2)^2 )/8)] I = (π^2 /(32))tan^(−1) (1+(π/2))−(π/(16)) +(1/4)ln [(1/2)+(((π+2)^2 )/8)] .](Q35803.png) | ||
| ||