calculate ∫_0 ^π {cos^8 x +sin^8 x}dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 79763 by mathmax by abdo last updated on 28/Jan/20
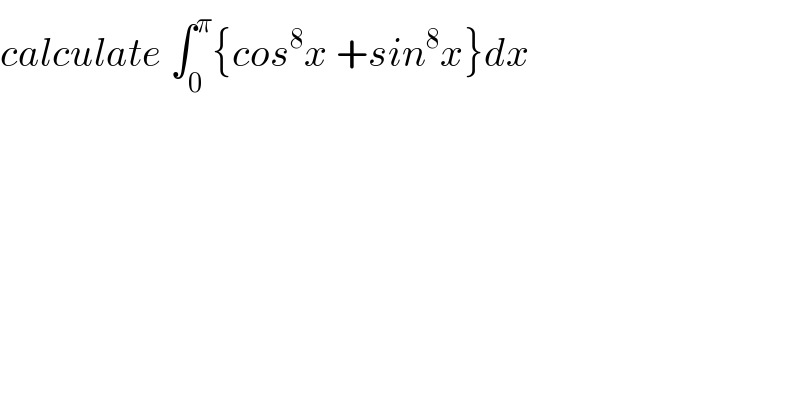
$calculate ∫_0 ^π {cos^8 x +sin^8 x}dx$
$c a l c u l a t e \int_{0}^{π} {{c o s}^{8} x + {s i n}^{8} x} d x$
Commented by john santu last updated on 28/Jan/20
$cos^8 x+sin^8 x=(sin^4 x)^2 +(cos^4 x)^2 = (sin^4 x+cos^4 x)^2 −2sin^4 xcos^4 x = {(sin^2 x+cos^2 x)^2 −2sin^2 xcos^2 x}^2 −(1/2)sin^2 (2x) = {1−(1/2)sin^2 (2x)}^2 −(1/2)sin^2 (2x) =1−(3/2)sin^2 (2x)+(1/4)sin^4 (2x) =1−(3/2)((1/2)−(1/2)cos (4x))+(1/4){(1/2)−(1/2)cos (4x)}^2 =(1/4)+(3/4)cos (4x)+(1/4){(1/4)−(1/2)cos (4x)+(1/4)cos^2 (4x)} = (5/(16))+(5/8)cos (4x)+(1/(16))((1/2)+(1/2)cos (8x)) = ((11)/(32))+(5/8)cos (4x)+(1/(32))cos (8x)$
$\cos^{8} x + \sin^{8} x = {(\sin^{4} x)}^{2} + {(\cos^{4} x)}^{2}$ $= {(\sin^{4} x + \cos^{4} x)}^{2} - 2 \sin^{4} xcos^{4} x$ $= {{(\sin^{2} x + \cos^{2} x)}^{2} - 2 \sin^{2} xcos^{2} x}^{2} - \frac{1}{2} \sin^{2} (2 x)$ $= {1 - \frac{1}{2} \sin^{2} (2 x)}^{2} - \frac{1}{2} \sin^{2} (2 x)$ $= 1 - \frac{3}{2} \sin^{2} (2 x) + \frac{1}{4} \sin^{4} (2 x)$ $= 1 - \frac{3}{2} (\frac{1}{2} - \frac{1}{2} \cos (4 x)) + \frac{1}{4} {\frac{1}{2} - \frac{1}{2} \cos (4 x)}^{2}$ $= \frac{1}{4} + \frac{3}{4} \cos (4 x) + \frac{1}{4} {\frac{1}{4} - \frac{1}{2} \cos (4 x) + \frac{1}{4} \cos^{2} (4 x)}$ $= \frac{5}{16} + \frac{5}{8} \cos (4 x) + \frac{1}{16} (\frac{1}{2} + \frac{1}{2} \cos (8 x))$ $= \frac{11}{32} + \frac{5}{8} \cos (4 x) + \frac{1}{32} \cos (8 x)$
Commented by john santu last updated on 28/Jan/20

$\underset{0}{\int^{π}} (\frac{11}{32} + \frac{5}{8} \cos (4 x) + \frac{1}{32} \cos (8 x)) dx =$ $\frac{11 x}{32} + \frac{5}{32} \sin (4 x) + \frac{1}{256} \sin (8 x) \underset{0}{\overset{π}{∣}}$ $= \frac{11 π}{32} ★$
	Answered by Henri Boucatchou last updated on 28/Jan/20

	$w e h a v e {c o s}^{8} x + {s i n}^{8} x = 1 - \frac{8}{8} {s i n}^{2} 2 x$ $= {c o s}^{2} 2 x = \frac{1}{4} {(e^{i 2 x} + e^{- i 2 x})}^{2}$ $= \frac{1}{4} [(e^{i 4 x} + e^{- i 4 x}) + 2] = \frac{1}{4} (2 c o s 4 x + 2)$ $\Rightarrow \int_{0}^{π} ({c o s}^{8} x + {s i n}^{8} x) d x = \frac{1}{2} {[\frac{1}{4} s i n 4 x + 2 x]}_{0}^{π}$ $= \frac{1}{2} (2 π)$ $= π$
	Commented by john santu last updated on 28/Jan/20

	$how to get \sin^{8} x + \cos^{8} x = 1 - \frac{8}{8} \sin^{2} 2 x ?$ $it impossible$
	Commented by john santu last updated on 28/Jan/20

	$a^{4} + b^{4} = {(a + b)}^{4} - 2 ab ({2 a}^{2} - 3 ab - {2 b}^{2})$ $put a = \cos^{2} x, b = \sin^{2} x$ $\cos^{8} x + \sin^{8} x = 1 - \frac{1}{2} . 4 \sin^{2} xcos^{2} x (2 (\cos^{2} x - \sin^{2} x) - \frac{3}{4} . 4 \sin^{2} xcos^{2} x)$ $= 1 - \frac{1}{2} \sin^{2} (2 x) (2 \cos (2 x) - \frac{3}{4} \sin^{2} (2 x))$ $= 1 - \frac{1}{4} \sin (4 x) \sin (2 x) + \frac{3}{8} \sin^{4} (2 x)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum