
Question and Answers Forum
Question Number 63033 by mathmax by abdo last updated on 28/Jun/19
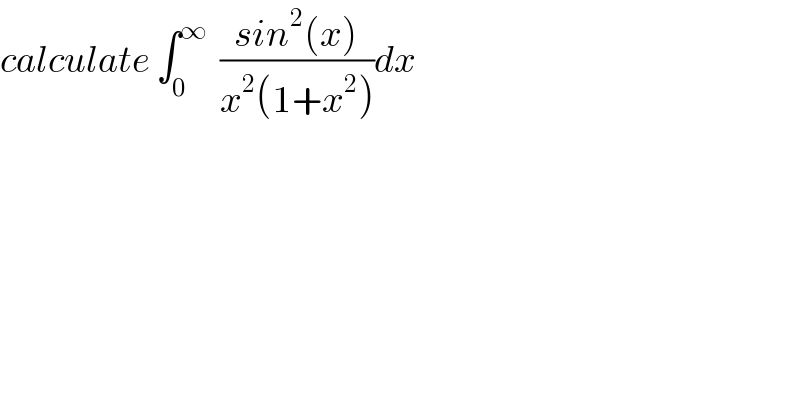
Commented by mathmax by abdo last updated on 28/Jun/19
![let A =∫_0 ^∞ ((sin^2 x)/(x^2 (1+x^2 ))) dx ⇒ A =∫_0 ^∞ sin^2 x{(1/x^2 ) −(1/(1+x^2 ))}dx =∫_0 ^∞ ((sin^2 x)/x^2 )dx −∫_0 ^∞ ((sin^2 x)/(1+x^2 ))dx =H−K by parts H =[−(1/x)sin^2 x]_0 ^(+∞) −∫_0 ^∞ −(1/x)2sinx cosxdx =∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sin(t))/(t/2)) (dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) (result proved) K =∫_0 ^∞ ((1−cos(2x))/(2(1+x^2 )))dx =(1/2)∫_0 ^∞ (dx/(1+x^2 )) −(1/2)∫_0 ^∞ ((cos(2x))/(1+x^2 ))dx =(π/4) −(1/4)∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(i2x) /(x^2 +1))dx) let W(z) =(e^(i2z) /(z^2 +1)) the poles of W are +^− i residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,i) =2iπ (e^(−2) /(2i)) =(π/e^2 ) ⇒ ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =(π/e^2 ) ⇒ K =(π/4)−(π/(4e^2 )) ⇒ A =(π/2) −(π/4) +(π/(4e^2 )) =(π/4) +(π/(4e^2 )) ⇒ A =(π/4)(1+(1/e^2 )).](Q63069.png)
| ||
Question and Answers Forum | ||
Question Number 63033 by mathmax by abdo last updated on 28/Jun/19 | ||
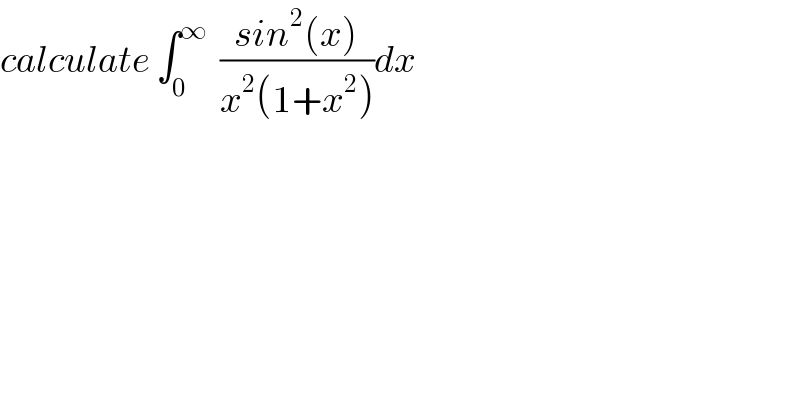 | ||
Commented by mathmax by abdo last updated on 28/Jun/19 | ||
![let A =∫_0 ^∞ ((sin^2 x)/(x^2 (1+x^2 ))) dx ⇒ A =∫_0 ^∞ sin^2 x{(1/x^2 ) −(1/(1+x^2 ))}dx =∫_0 ^∞ ((sin^2 x)/x^2 )dx −∫_0 ^∞ ((sin^2 x)/(1+x^2 ))dx =H−K by parts H =[−(1/x)sin^2 x]_0 ^(+∞) −∫_0 ^∞ −(1/x)2sinx cosxdx =∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sin(t))/(t/2)) (dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) (result proved) K =∫_0 ^∞ ((1−cos(2x))/(2(1+x^2 )))dx =(1/2)∫_0 ^∞ (dx/(1+x^2 )) −(1/2)∫_0 ^∞ ((cos(2x))/(1+x^2 ))dx =(π/4) −(1/4)∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(i2x) /(x^2 +1))dx) let W(z) =(e^(i2z) /(z^2 +1)) the poles of W are +^− i residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,i) =2iπ (e^(−2) /(2i)) =(π/e^2 ) ⇒ ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =(π/e^2 ) ⇒ K =(π/4)−(π/(4e^2 )) ⇒ A =(π/2) −(π/4) +(π/(4e^2 )) =(π/4) +(π/(4e^2 )) ⇒ A =(π/4)(1+(1/e^2 )).](Q63069.png) | ||