
Question and Answers Forum
Question Number 42809 by maxmathsup by imad last updated on 02/Sep/18
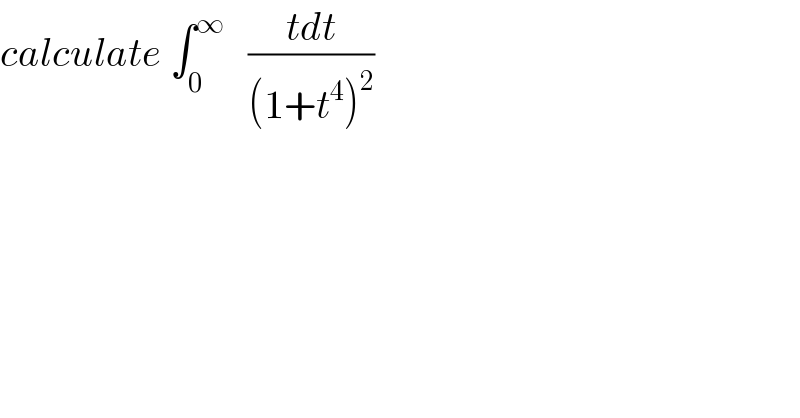
Commented by prof Abdo imad last updated on 03/Sep/18
![let A = ∫_0 ^∞ ((tdt)/((1+t^4 )^2 )) changement t^2 =x give 2tdt =dx ⇒A =∫_0 ^∞ (dx/(2(1+x^2 )^2 )) =_(x=tanθ) (1/2) ∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 )) dθ=(1/2) ∫_0 ^(π/2) cos^2 θ dθ =(1/4) ∫_0 ^(π/2) (1+cos(2θ))dθ =(π/8) + (1/8)[sin(2θ)]_0 ^(π/2) =(π/8) +0 ⇒A =(π/8) .](Q42849.png)
Answered by sma3l2996 last updated on 03/Sep/18
![A=∫_0 ^∞ ((tdt)/((1+t^4 )^2 )) t^2 =x⇒dx=2tdt A=(1/2)∫_0 ^∞ (dx/((1+x^2 )^2 )) by parts u=(1/((1+x^2 )^2 ))⇒u′=((−2×2x)/((1+x^2 ))) v=1⇒v′=x A=(1/2)[(x/((1+x^2 )^2 ))]_0 ^∞ +2∫_0 ^∞ (x^2 /(1+x^2 ))dx=2∫_0 ^∞ (1−(1/(1+x^2 )))dx A=2[x−tan^(−1) (x)]_0 ^∞ A=+∞](Q42822.png)
| ||
Question and Answers Forum | ||
Question Number 42809 by maxmathsup by imad last updated on 02/Sep/18 | ||
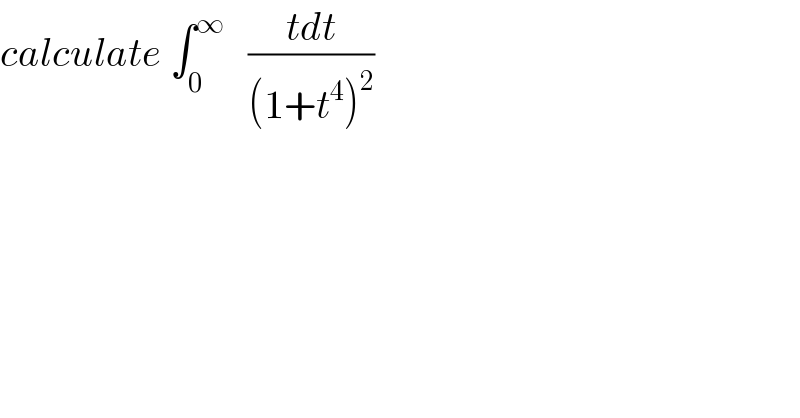 | ||
Commented by prof Abdo imad last updated on 03/Sep/18 | ||
![let A = ∫_0 ^∞ ((tdt)/((1+t^4 )^2 )) changement t^2 =x give 2tdt =dx ⇒A =∫_0 ^∞ (dx/(2(1+x^2 )^2 )) =_(x=tanθ) (1/2) ∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 )) dθ=(1/2) ∫_0 ^(π/2) cos^2 θ dθ =(1/4) ∫_0 ^(π/2) (1+cos(2θ))dθ =(π/8) + (1/8)[sin(2θ)]_0 ^(π/2) =(π/8) +0 ⇒A =(π/8) .](Q42849.png) | ||
Answered by sma3l2996 last updated on 03/Sep/18 | ||
![A=∫_0 ^∞ ((tdt)/((1+t^4 )^2 )) t^2 =x⇒dx=2tdt A=(1/2)∫_0 ^∞ (dx/((1+x^2 )^2 )) by parts u=(1/((1+x^2 )^2 ))⇒u′=((−2×2x)/((1+x^2 ))) v=1⇒v′=x A=(1/2)[(x/((1+x^2 )^2 ))]_0 ^∞ +2∫_0 ^∞ (x^2 /(1+x^2 ))dx=2∫_0 ^∞ (1−(1/(1+x^2 )))dx A=2[x−tan^(−1) (x)]_0 ^∞ A=+∞](Q42822.png) | ||
| ||