
Question and Answers Forum
Question Number 64904 by mathmax by abdo last updated on 23/Jul/19
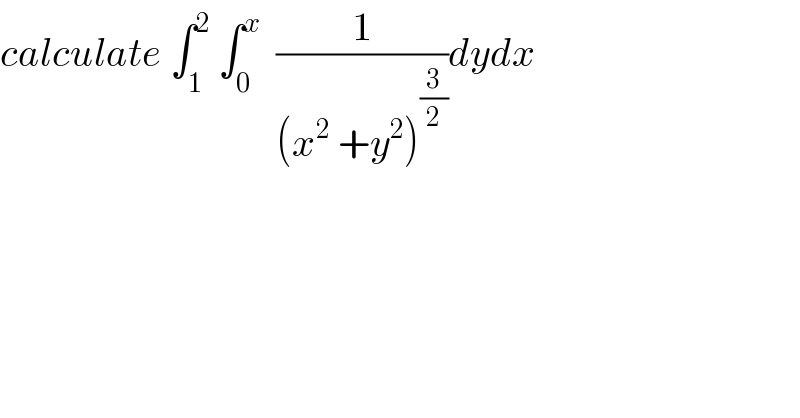
Commented by ~ À ® @ 237 ~ last updated on 23/Jul/19
![le domaine d integration D ={(x . y) / 1<x<2 0<y<x} en posant x=u et y=utanv on a J(x y)=utanv(1+tan^2 v) D={(u. utanv)/ 1<u<2 et 0<tanv<1} ={(u. utanv)/ 1<u<2 et 0<v<(π/4) } on obtient alors I= ∫_1 ^2 ∫_0 ^(π/4) ((utanv(1+tan^2 v)dudv)/(((√((u^2 +u^2 tan^2 v))))^3 )) =∫_1 ^2 (1/u^2 )du ∫_0 ^(π/4) ((tanv(1+tan^2 v)dv)/((1+tan^2 v)^(3/2) )) =[−(1/u)]_1 ^2 [(1/2) ((−1)/(((3/2)−1)(1+tan^2 v)^(((3/2)−1)) ))]_0 ^(π/4) = = (((2−(√2)))/4)](Q64976.png)
Commented by mathmax by abdo last updated on 23/Jul/19

| ||
Question and Answers Forum | ||
Question Number 64904 by mathmax by abdo last updated on 23/Jul/19 | ||
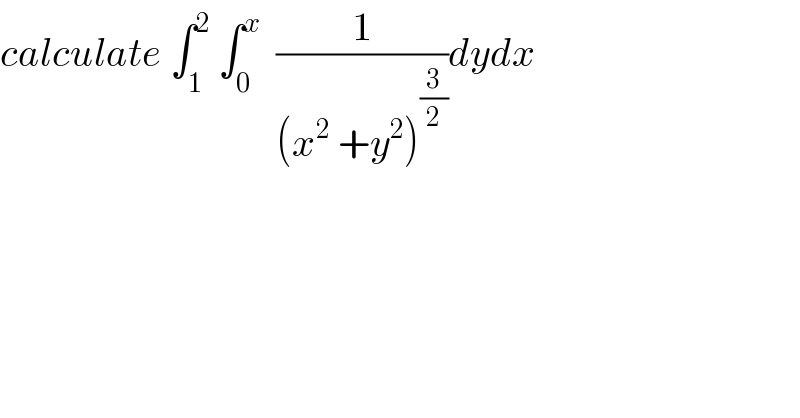 | ||
Commented by ~ À ® @ 237 ~ last updated on 23/Jul/19 | ||
![le domaine d integration D ={(x . y) / 1<x<2 0<y<x} en posant x=u et y=utanv on a J(x y)=utanv(1+tan^2 v) D={(u. utanv)/ 1<u<2 et 0<tanv<1} ={(u. utanv)/ 1<u<2 et 0<v<(π/4) } on obtient alors I= ∫_1 ^2 ∫_0 ^(π/4) ((utanv(1+tan^2 v)dudv)/(((√((u^2 +u^2 tan^2 v))))^3 )) =∫_1 ^2 (1/u^2 )du ∫_0 ^(π/4) ((tanv(1+tan^2 v)dv)/((1+tan^2 v)^(3/2) )) =[−(1/u)]_1 ^2 [(1/2) ((−1)/(((3/2)−1)(1+tan^2 v)^(((3/2)−1)) ))]_0 ^(π/4) = = (((2−(√2)))/4)](Q64976.png) | ||
Commented by mathmax by abdo last updated on 23/Jul/19 | ||
 | ||