
Question and Answers Forum
Question Number 42802 by maxmathsup by imad last updated on 02/Sep/18
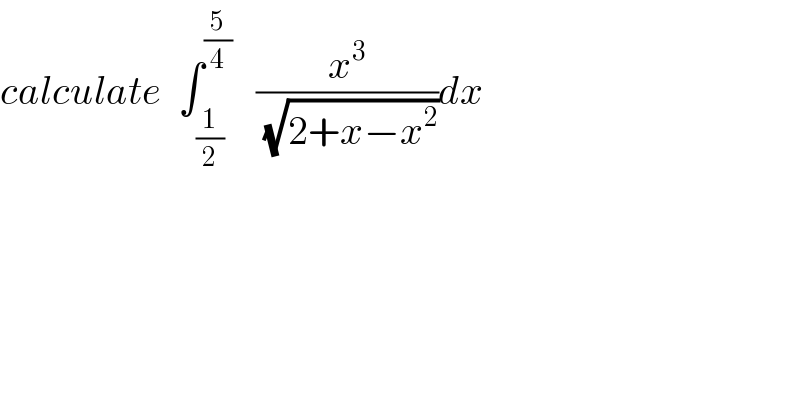
Commented by maxmathsup by imad last updated on 05/Sep/18
![let A = ∫_(1/2) ^(5/4) (x^3 /(√(2+x−x^2 )))dx⇒A = ∫_(1/2) ^(5/4) (x^3 /(√(−x^2 +x+2)))dx we have −x^2 +x+2 =−(x^2 −x−2) =−(x^2 −2(1/2)x +(1/4)−(1/4)−2) =−{(x−(1/2))^2 −(9/4)}=(9/4) −(x−(1/2))^2 ⇒A = ∫_(1/2) ^(5/4) (x^3 /(√((9/4)−(x−(1/2))^2 )))dx =_(x−(1/2) =(3/2)sint) ∫_0 ^(π/6) ((((1/2)+(3/2)sint)^3 )/((3/2) cost)) (3/2) cost dt = ∫_0 ^(π/6) (3sint +1)^3 dt =∫_0 ^(π/6) (27sin^3 t +27sin^2 t +9sint +1)dt =27 ∫_0 ^(π/6) sin^3 t dt +27 ∫_0 ^(π/6) sin^2 t dt +9 ∫_0 ^(π/6) sint dt +(π/6) but ∫_0 ^(π/6) sint dt =[−cost]_0 ^(π/6) =1−((√3)/2) ∫_0 ^(π/6) sin^2 t dt =(1/2) ∫_0 ^(π/6) (1−cos(2t))dt=(π/(12)) −(1/4)[sin(2t)]_0 ^(π/6) =(π/(12)) −(1/4) ((√3)/2) =(π/(12)) −((√3)/8) we have sin^3 t ={((e^(it) −e^(−it) )/(2i))}^3 =−(1/(8i)){ Σ_(k=0) ^3 C_3 ^k e^(ikt) (−1)^(3−k) e^(−i(3−k)t) } =(i/8){ −e^(−i3t) +3 e^(it) e^(−i2t) − 3 e^(i2t) e^(−it) +e^(i3t) } =(i/8){e^(i3t) −e^(−i3t) −3(e^(it) −e^(−it) )} =(i/8){2i sin(3t) −6i sin(t)} =−(1/4)sin(3t) +(3/4) sin(t) ⇒ ∫_0 ^(π/6) sin^3 t dt =(3/4) ∫_0 ^(π/6) sin(t)dt−(1/4) ∫_0 ^(π/6) sin(3t)dt =−(3/4)[cost]_0 ^(π/6) +(1/(12))[ cos(3t)]_0 ^(π/6) =−(3/4)(((√3)/2)−1) +(1/(12))( −1) =(3/4) −((3(√3))/8) −(1/(12)) so the value of A is known .](Q42928.png)
| ||
Question and Answers Forum | ||
Question Number 42802 by maxmathsup by imad last updated on 02/Sep/18 | ||
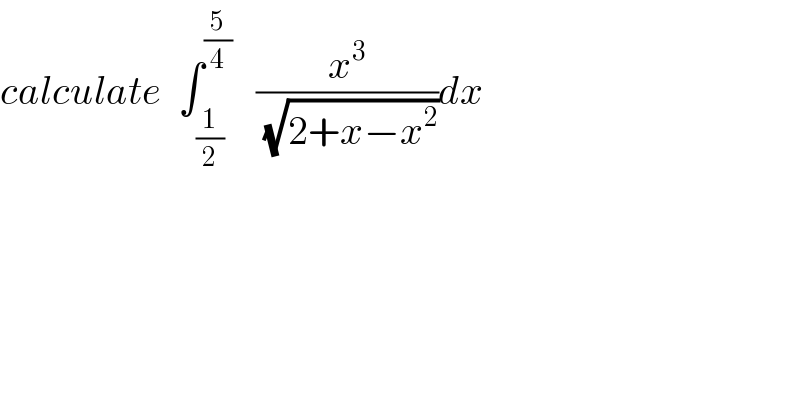 | ||
Commented by maxmathsup by imad last updated on 05/Sep/18 | ||
![let A = ∫_(1/2) ^(5/4) (x^3 /(√(2+x−x^2 )))dx⇒A = ∫_(1/2) ^(5/4) (x^3 /(√(−x^2 +x+2)))dx we have −x^2 +x+2 =−(x^2 −x−2) =−(x^2 −2(1/2)x +(1/4)−(1/4)−2) =−{(x−(1/2))^2 −(9/4)}=(9/4) −(x−(1/2))^2 ⇒A = ∫_(1/2) ^(5/4) (x^3 /(√((9/4)−(x−(1/2))^2 )))dx =_(x−(1/2) =(3/2)sint) ∫_0 ^(π/6) ((((1/2)+(3/2)sint)^3 )/((3/2) cost)) (3/2) cost dt = ∫_0 ^(π/6) (3sint +1)^3 dt =∫_0 ^(π/6) (27sin^3 t +27sin^2 t +9sint +1)dt =27 ∫_0 ^(π/6) sin^3 t dt +27 ∫_0 ^(π/6) sin^2 t dt +9 ∫_0 ^(π/6) sint dt +(π/6) but ∫_0 ^(π/6) sint dt =[−cost]_0 ^(π/6) =1−((√3)/2) ∫_0 ^(π/6) sin^2 t dt =(1/2) ∫_0 ^(π/6) (1−cos(2t))dt=(π/(12)) −(1/4)[sin(2t)]_0 ^(π/6) =(π/(12)) −(1/4) ((√3)/2) =(π/(12)) −((√3)/8) we have sin^3 t ={((e^(it) −e^(−it) )/(2i))}^3 =−(1/(8i)){ Σ_(k=0) ^3 C_3 ^k e^(ikt) (−1)^(3−k) e^(−i(3−k)t) } =(i/8){ −e^(−i3t) +3 e^(it) e^(−i2t) − 3 e^(i2t) e^(−it) +e^(i3t) } =(i/8){e^(i3t) −e^(−i3t) −3(e^(it) −e^(−it) )} =(i/8){2i sin(3t) −6i sin(t)} =−(1/4)sin(3t) +(3/4) sin(t) ⇒ ∫_0 ^(π/6) sin^3 t dt =(3/4) ∫_0 ^(π/6) sin(t)dt−(1/4) ∫_0 ^(π/6) sin(3t)dt =−(3/4)[cost]_0 ^(π/6) +(1/(12))[ cos(3t)]_0 ^(π/6) =−(3/4)(((√3)/2)−1) +(1/(12))( −1) =(3/4) −((3(√3))/8) −(1/(12)) so the value of A is known .](Q42928.png) | ||