
Question and Answers Forum
Question Number 40153 by maxmathsup by imad last updated on 16/Jul/18
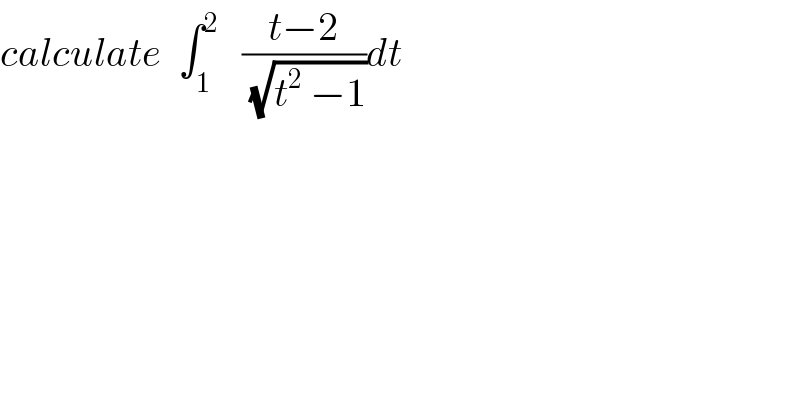
Commented by maxmathsup by imad last updated on 17/Jul/18
![I = ∫_1 ^2 ((tdt)/(√(t^2 −1)))dt −2 ∫_1 ^2 (dt/(√(t^2 −1))) but ∫_1 ^2 (t/(√(t^2 −1)))dt =[(√(t^2 −1))]_1 ^2 =(√3) also changement t=chu give ∫ (dt/(√(t^2 −1))) =∫ ((shu du)/(shu)) = u +c = argch(t)=ln(t+(√(t^2 −1)))+c ⇒ ∫_1 ^2 (dt/(√(t^2 −1))) =[ln(t+(√(t^2 −1)))]_1 ^2 =ln(2+(√3)) ⇒ I =(√3) −2ln(2+(√3)) .](Q40203.png)
Answered by sma3l2996 last updated on 16/Jul/18
![∫_1 ^2 ((t−2)/(√(t^2 −1)))dt=∫_1 ^2 (t/(√(t^2 −1)))dt−2∫_1 ^2 (dt/(√(t^2 −1))) =[(√(t^2 −1))]_1 ^2 −2∫_1 ^2 ((t+(√(t^2 −1)))/((t+(√(t^2 −1)))(√(t^2 −1))))dt =(√5)−2∫_1 ^2 ((t+(√(t^2 −1)))/(√(t^2 −1)))×(dt/(t+(√(t^2 −1)))) =(√5)−2∫_1 ^2 ((t/(√(t^2 −1)))+1)×(1/(t+(√(t^2 −1))))dt =(√5)−2∫_1 ^2 ((d(t+(√(t^2 −1))))/(t+(√(t^2 −1)))) =(√5)−2[ln∣t+(√(t^2 −1))∣]_1 ^2 =(√5)−2ln(2+(√5))](Q40162.png)
| ||
Question and Answers Forum | ||
Question Number 40153 by maxmathsup by imad last updated on 16/Jul/18 | ||
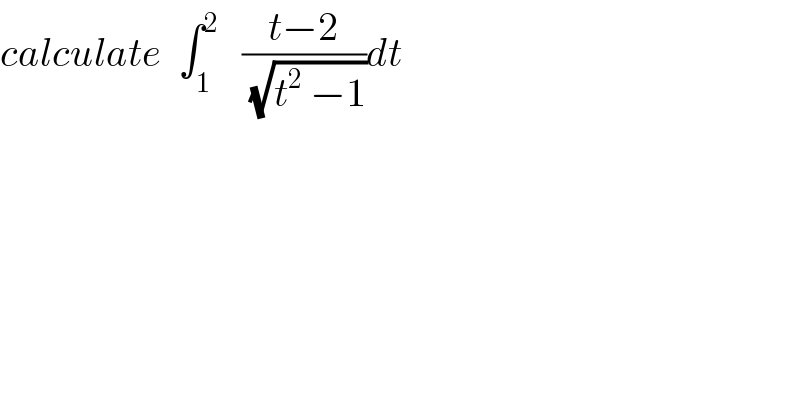 | ||
Commented by maxmathsup by imad last updated on 17/Jul/18 | ||
![I = ∫_1 ^2 ((tdt)/(√(t^2 −1)))dt −2 ∫_1 ^2 (dt/(√(t^2 −1))) but ∫_1 ^2 (t/(√(t^2 −1)))dt =[(√(t^2 −1))]_1 ^2 =(√3) also changement t=chu give ∫ (dt/(√(t^2 −1))) =∫ ((shu du)/(shu)) = u +c = argch(t)=ln(t+(√(t^2 −1)))+c ⇒ ∫_1 ^2 (dt/(√(t^2 −1))) =[ln(t+(√(t^2 −1)))]_1 ^2 =ln(2+(√3)) ⇒ I =(√3) −2ln(2+(√3)) .](Q40203.png) | ||
Answered by sma3l2996 last updated on 16/Jul/18 | ||
![∫_1 ^2 ((t−2)/(√(t^2 −1)))dt=∫_1 ^2 (t/(√(t^2 −1)))dt−2∫_1 ^2 (dt/(√(t^2 −1))) =[(√(t^2 −1))]_1 ^2 −2∫_1 ^2 ((t+(√(t^2 −1)))/((t+(√(t^2 −1)))(√(t^2 −1))))dt =(√5)−2∫_1 ^2 ((t+(√(t^2 −1)))/(√(t^2 −1)))×(dt/(t+(√(t^2 −1)))) =(√5)−2∫_1 ^2 ((t/(√(t^2 −1)))+1)×(1/(t+(√(t^2 −1))))dt =(√5)−2∫_1 ^2 ((d(t+(√(t^2 −1))))/(t+(√(t^2 −1)))) =(√5)−2[ln∣t+(√(t^2 −1))∣]_1 ^2 =(√5)−2ln(2+(√5))](Q40162.png) | ||
| ||