
Question and Answers Forum
Question Number 36182 by prof Abdo imad last updated on 30/May/18
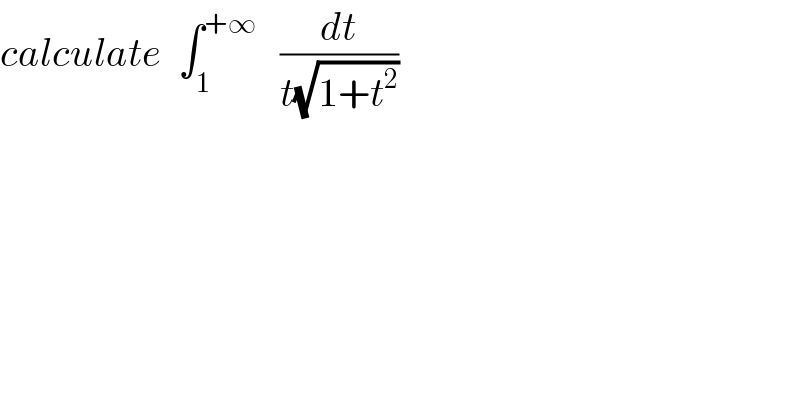
Commented by maxmathsup by imad last updated on 15/Aug/18
![let I = ∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) dt changement t =sh(x) give I = ∫_(argsh(1)) ^(+∞) (1/(sh(x)ch(x))) ch(x)dx = ∫_(ln(1+(√2))) ^(+∞) (dx/(sh(x))) = ∫_(ln(1+(√2))) ^(+∞) ((2dx)/(e^x −e^(−x) )) = ∫_(ln(1+(√2))) ^(+∞) ((2 e^x )/(e^(2x) −1))dx =_(e^x =u) ∫_(1+(√2)) ^(+∞) ((2u)/(u^2 −1)) (du/u) = ∫_(1+(√2)) ^(+∞) ((2du)/(u^2 −1)) = ∫_(1+(√2)) ^(+∞) ( (1/(u−1)) −(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_(1+(√2)) ^(+∞) =−ln∣ ((√2)/(2+(√2))) ∣ =−ln(((√2)/(√(2(1+(√2))))))=ln(1+(√2)) ⇒ I =ln(1+(√2)) .](Q41951.png)
Answered by sma3l2996 last updated on 31/May/18
![L=∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) let t=sinhx⇒dt=coshxdx L=∫_(ln((√2)+1)) ^(+∞) ((coshx)/(sinhx(√(1+sinh^2 x))))dx =∫_(ln((√2)+1)) ^(+∞) (dx/(sinh(x)))=2∫_(ln((√2)+1)) ^(+∞) (e^x /(e^(2x) −1))dx u=e^x ⇒du=e^x dx L=2∫_((√2)+1) ^(+∞) (du/(u^2 −1))=2∫_((√2)+1) ^(+∞) (du/((u+1)(u−1))) =∫_((√2)+1) ^(+∞) ((1/(u−1))−(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_((√2)+1) ^(+∞) =ln∣(((√2)+2)/(√2))∣= L=ln((√2)+1)](Q36273.png)
Answered by ajfour last updated on 31/May/18

| ||
Question and Answers Forum | ||
Question Number 36182 by prof Abdo imad last updated on 30/May/18 | ||
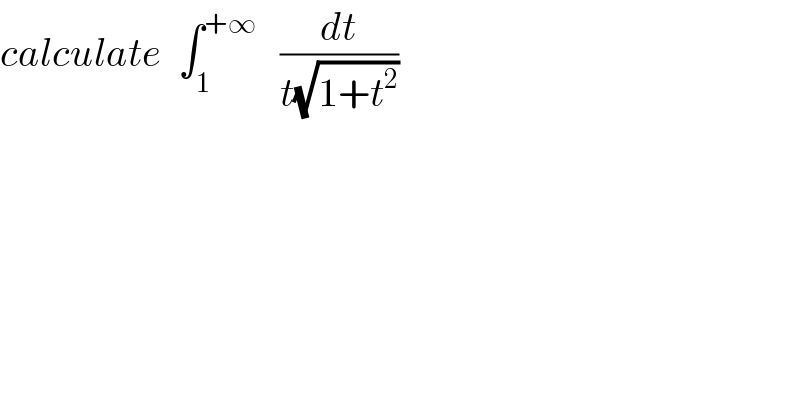 | ||
Commented by maxmathsup by imad last updated on 15/Aug/18 | ||
![let I = ∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) dt changement t =sh(x) give I = ∫_(argsh(1)) ^(+∞) (1/(sh(x)ch(x))) ch(x)dx = ∫_(ln(1+(√2))) ^(+∞) (dx/(sh(x))) = ∫_(ln(1+(√2))) ^(+∞) ((2dx)/(e^x −e^(−x) )) = ∫_(ln(1+(√2))) ^(+∞) ((2 e^x )/(e^(2x) −1))dx =_(e^x =u) ∫_(1+(√2)) ^(+∞) ((2u)/(u^2 −1)) (du/u) = ∫_(1+(√2)) ^(+∞) ((2du)/(u^2 −1)) = ∫_(1+(√2)) ^(+∞) ( (1/(u−1)) −(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_(1+(√2)) ^(+∞) =−ln∣ ((√2)/(2+(√2))) ∣ =−ln(((√2)/(√(2(1+(√2))))))=ln(1+(√2)) ⇒ I =ln(1+(√2)) .](Q41951.png) | ||
Answered by sma3l2996 last updated on 31/May/18 | ||
![L=∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) let t=sinhx⇒dt=coshxdx L=∫_(ln((√2)+1)) ^(+∞) ((coshx)/(sinhx(√(1+sinh^2 x))))dx =∫_(ln((√2)+1)) ^(+∞) (dx/(sinh(x)))=2∫_(ln((√2)+1)) ^(+∞) (e^x /(e^(2x) −1))dx u=e^x ⇒du=e^x dx L=2∫_((√2)+1) ^(+∞) (du/(u^2 −1))=2∫_((√2)+1) ^(+∞) (du/((u+1)(u−1))) =∫_((√2)+1) ^(+∞) ((1/(u−1))−(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_((√2)+1) ^(+∞) =ln∣(((√2)+2)/(√2))∣= L=ln((√2)+1)](Q36273.png) | ||
| ||
Answered by ajfour last updated on 31/May/18 | ||
 | ||
| ||