Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 116245 by mathmax by abdo last updated on 02/Oct/20

$$\mathrm{calculate}{\int }_1^{\mathrm{\infty }}\frac{\mathrm{dx}}{{({2\mathrm{x}}^2-1)}^5}$$

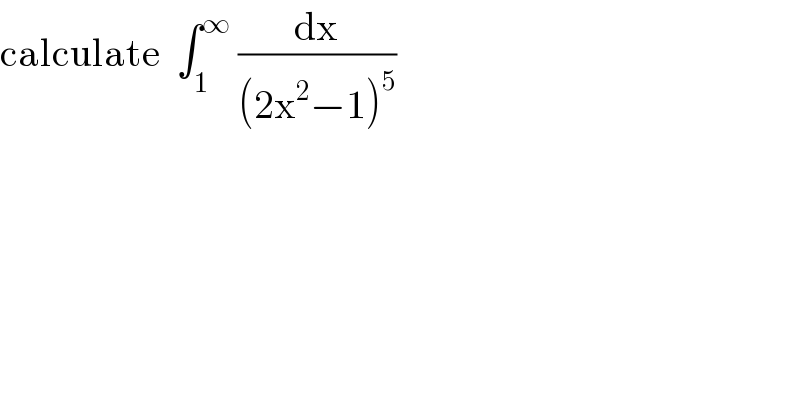
Answered by MJS_new last updated on 02/Oct/20

$$\int \frac{dx}{{(2x^2-1)}^5}=$$$$\left[\mathrm{Ostrogradski}\right]$$$$=\frac{x(840x^6-1540x^4+1022x^2-279)}{384{(2x^2-1)}^4}+\frac{35}{128}\int \frac{dx}{2x^2-1}=$$$$=\frac{x(840x^6-1540x^4+1022x^2-279)}{384{(2x^2-1)}^4}+\frac{35\sqrt{2}}{512}\ln \frac{\sqrt{2}x-1}{\sqrt{2}x+1}+C$$$$\Rightarrow$$$$\underset{1}{\stackrel{\mathrm{\infty }}{\int }}\frac{dx}{{(2x^2-1)}^5}=-\frac{43}{384}+\frac{35\sqrt{2}}{256}\ln (1+\sqrt{2})$$

Commented by Bird last updated on 02/Oct/20

$$thankyousir$$

Answered by 1549442205PVT last updated on 03/Oct/20

$$\frac{2}{{2\mathrm{x}}^2-1}=\frac{1}{\sqrt{2}\mathrm{x}-1}-\frac{1}{\sqrt{2}\mathrm{x}+1}.\mathrm{Hence},$$$$\mathrm{Put}\frac{1}{\sqrt{2}\mathrm{x}-1}=\mathrm{a},\frac{1}{\sqrt{2}\mathrm{x}+1}=\mathrm{b}\Rightarrow 2\mathrm{ab}=\mathrm{a}-\mathrm{b}$$$$\frac{1}{{({2\mathrm{x}}^2-1)}^5}=\frac{1}{32}\times {\left(\frac{2}{{2\mathrm{x}}^2-1}\right)}^5=\frac{1}{32}{(\mathrm{a}-\mathrm{b})}^5$$$$\mathrm{We}\mathrm{have}{(\mathrm{a}-\mathrm{b})}^5$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-5\mathrm{ab}({\mathrm{a}}^3-{\mathrm{b}}^3)+10{\left(\mathrm{ab}\right)}^2(\mathrm{a}-\mathrm{b})$$$${\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}(\mathrm{a}-\mathrm{b})({\mathrm{a}}^3-{\mathrm{b}}^3)+\frac{10}{4}{(\mathrm{a}-\mathrm{b})}^3$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}({\mathrm{a}}^4+{\mathrm{b}}^4)+\frac{5}{2}\mathrm{ab}({\mathrm{a}}^2+{\mathrm{b}}^2)+\frac{5}{2}[{\mathrm{a}}^3-{\mathrm{b}}^3-3\mathrm{ab}(\mathrm{a}-\mathrm{b})]$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}({\mathrm{a}}^4+{\mathrm{b}}^4)+\frac{5}{4}(\mathrm{a}-\mathrm{b})({\mathrm{a}}^2+{\mathrm{b}}^2)+\frac{5}{2}[{\mathrm{a}}^3-{\mathrm{b}}^3-3\mathrm{ab}(\mathrm{a}-\mathrm{b})]]$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}({\mathrm{a}}^4+{\mathrm{b}}^4)+\frac{5}{4}({\mathrm{a}}^3-{\mathrm{b}}^3)-\frac{5}{4}\mathrm{ab}(\mathrm{a}-\mathrm{b})+\frac{5}{2}[{\mathrm{a}}^3-{\mathrm{b}}^3-3\mathrm{ab}(\mathrm{a}-\mathrm{b})]]$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}({\mathrm{a}}^4+{\mathrm{b}}^4)+\frac{15}{4}({\mathrm{a}}^3-{\mathrm{b}}^3)-\frac{35}{8}{(\mathrm{a}-\mathrm{b})}^2$$$$={\mathrm{a}}^5-{\mathrm{b}}^5-\frac{5}{2}({\mathrm{a}}^4+{\mathrm{b}}^4)+\frac{15}{4}({\mathrm{a}}^3-{\mathrm{b}}^3)-\frac{35}{8}({\mathrm{a}}^2+{\mathrm{b}}^2)+\frac{35}{8}(\mathrm{a}-\mathrm{b})$$$$\mathrm{I}={\int }_1^{\mathrm{\infty }}[\frac{1}{32{(\sqrt{2}\mathrm{x}-1)}^5}-\frac{1}{32{(\sqrt{2}\mathrm{x}+1)}^5}-\frac{5}{64{(\sqrt{2}\mathrm{x}-1)}^4}$$$$-\frac{5}{64{(\sqrt{2}\mathrm{x}+1)}^4}+\frac{15}{128{(\sqrt{2}\mathrm{x}-1)}^3}-\frac{15}{128{(\sqrt{2}\mathrm{x}+1)}^3}$$$$-\frac{35}{256{(\sqrt{2}\mathrm{x}-1)}^2}-\frac{35}{256{(\sqrt{2}\mathrm{x}+1)}^2}+\frac{35}{256}(\mathrm{a}-\mathrm{b})]\mathrm{dx}$$$$\mathrm{Put}\sqrt{2}\mathrm{x}-1=\mathrm{u},\sqrt{2}\mathrm{x}+1=\mathrm{v}\Rightarrow \sqrt{2}\mathrm{dx}=\mathrm{du}=\mathrm{dv}.\mathrm{Hence},$$$$\mathrm{I}=-\frac{1}{128\sqrt{2}{(\sqrt{2}\mathrm{x}-1)}^4}+\frac{1}{128\sqrt{2}{(\sqrt{2}\mathrm{x}+1)}^4}$$$$+\frac{5}{192\sqrt{2}{(\sqrt{2}\mathrm{x}-1)}^3}+\frac{5}{192\sqrt{2}{(\sqrt{2}\mathrm{x}+1)}^3}$$$$-\frac{15}{256\sqrt{2}{(\sqrt{2}\mathrm{x}-1)}^2}+\frac{15}{256\sqrt{2}{(\sqrt{2}\mathrm{x}+1)}^2}$$$${+\frac{35}{256\sqrt{2}(\sqrt{2}\mathrm{x}-1)}+\frac{35}{256\sqrt{2}(\sqrt{2}\mathrm{x}+1)}]}_1^{\mathrm{\infty }}$$$$+\frac{35}{256\sqrt{2}}\ln \mid \frac{\sqrt{2}\mathrm{x}-1}{\sqrt{2}\mathrm{x}+1}\mid$$$$=[\frac{-(16\sqrt{2}{\mathrm{x}}^3+8\sqrt{2}\mathrm{x})}{128\sqrt{2}{({2\mathrm{x}}^2-1)}^4}+\frac{5(4\sqrt{2}{\mathrm{x}}^3+6\sqrt{2}\mathrm{x})}{192\sqrt{2}{({2\mathrm{x}}^2-1)}^3}$$$${-\frac{15\times \left(4\sqrt{2}\mathrm{x}\right)}{256\sqrt{2}{({2\mathrm{x}}^2-1)}^2}+\frac{35\times 2\sqrt{2}\mathrm{x}}{256\sqrt{2}({2\mathrm{x}}^2-1)}+\frac{35}{256\sqrt{2}}\ln \mid \frac{\sqrt{2}\mathrm{x}-1}{\sqrt{2}\mathrm{x}+1}\mid ]}_1^{\mathrm{\infty }}$$$$=-(\frac{-24\sqrt{2}}{128\sqrt{2}}+\frac{50\sqrt{2}}{192\sqrt{2}}-\frac{60\sqrt{2}}{256\sqrt{2}}+\frac{70\sqrt{2}}{256\sqrt{2}}+\frac{35}{256}\ln \frac{\sqrt{2}-1}{\sqrt{2}+1})$$$$=-\frac{43}{384}-\frac{35\sqrt{2}}{256}\ln (\sqrt{2}-1)\approx 0.058434$$

Commented by Bird last updated on 02/Oct/20

$$thankyousirforthishardwork$$

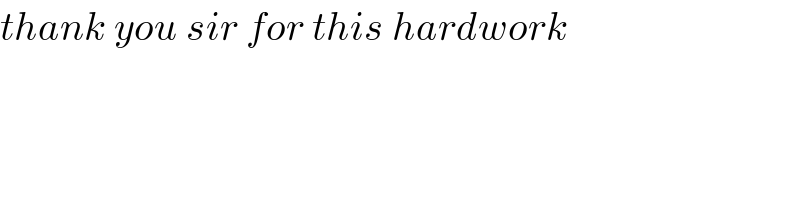
Commented by 1549442205PVT last updated on 03/Oct/20

$$\mathrm{Thank}\mathrm{Sir}.\mathrm{You}\mathrm{are}\mathrm{welcome}.$$

Answered by Bird last updated on 03/Oct/20

$$I={\int }_1^{\mathrm{\infty }}\frac{dx}{{(2x^2-1)}^5}\Rightarrow$$$$I={\int }_1^{\mathrm{\infty }}\frac{dx}{{(x\sqrt{2}-1)}^5{(x\sqrt{2}+1)}^5}$$$$={\int }_1^{\mathrm{\infty }}\frac{dx}{{\left(\frac{x\sqrt{2}-1}{x\sqrt{2}+1}\right)}^5{(x\sqrt{2}+1)}^{10}}$$$$wedothechangement\frac{x\sqrt{2}-1}{x\sqrt{2}+1}=t$$$$\Rightarrow x\sqrt{2}-1=tx\sqrt{2}+t\Rightarrow$$$$(\sqrt{2}-t\sqrt{2})x=t+1\Rightarrow x=\frac{t+1}{\sqrt{2}(1-t)}$$$$\Rightarrow \frac{dx}{dt}=\frac{1}{\sqrt{2}}.\frac{1-t-(t+1)(-1)}{{(1-t)}^2}$$$$=\frac{1}{\sqrt{2}}.\frac{2}{{(t-1)}^2}alsox\sqrt{2}+1=\frac{t+1}{1-t}+1$$$$=\frac{t+1+1-t}{1-t}=\frac{2}{1-t}\Rightarrow$$$$\Rightarrow I={\int }_{\frac{\sqrt{2}-1}{\sqrt{2}+1}}^1\frac{1}{t^5{\left(\frac{2}{1-t}\right)}^{10}}\times \frac{\sqrt{2}}{{(t-1)}^2}dt$$$$=\frac{\sqrt{2}}{2^{10}}{\int }_{3-2\sqrt{2}}^1\frac{{(t-1)}^8}{t^5}dt$$$$=\frac{\sqrt{2}}{2^{10}}{\int }_{3-2\sqrt{2}}^1\frac{\sum _{k=0}^8{C}_8^k{t}^k{(-1)}^{8-k}}{t^5}dt$$$$=\frac{\sqrt{2}}{2^{10}}\sum _{k=0}^8{(-1)}^k{C}_8^k{\int }_{3-2\sqrt{2}}^1{t}^{k-5}dt$$$$=\frac{\sqrt{2}}{2^{10}}\sum _{k=0andk\ne 4}^8{(-1)}^k{C}_8^k{\left[\frac{1}{k-4}{t}^{k-4}\right]}_{3-2\sqrt{2}}^1$$$$+\frac{\sqrt{2}}{2^{10}}{C}_8^4{\left[lnt\right]}_{3-2\sqrt{2}}^1$$$$I=\frac{\sqrt{2}}{2^{10}}\sum _{k=0andk\ne 4}^8\frac{{(-1)}^k{C}_8^k}{k-4}\{1-{(3-2\sqrt{2})}^{k-4}\}$$$$-\frac{\sqrt{2}}{2^{10}}{C}_8^{k}ln(3-2\sqrt{2})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com