
Question and Answers Forum
Question Number 32301 by abdo imad last updated on 22/Mar/18
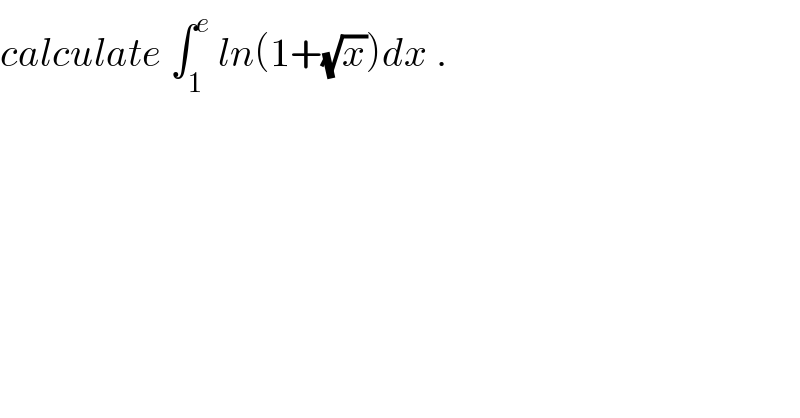
Commented by abdo imad last updated on 01/Apr/18
![ch. (√x) =t give I = ∫_1 ^(√e) (2t) ln(1+t)dt .by parts I =( [ t^2 ln(1+t)]_1 ^(√e) − ∫_1 ^(√e) (t^2 /(1+t))dt) =( e ln(1+(√e)) −ln(2) ) − ∫_1 ^(√e) ((t^2 −1+1)/(1+t))dt ∫_1 ^(√e) ((t^2 −1+1)/(1+t)) dt = ∫_1 ^(√e) (t−1) dt +∫_1 ^(√e) (dt/(1+t)) =[(t^2 /2) −t]_1 ^(√e) +[ln(1+t)]_1 ^(√e) =(e/2) −(√e) −(1/2) +1 +ln(1+(√e)) −ln(2) =(e/2) −(√e) +(1/2) +ln(1+(√e)) −ln(2) I =e ln(1+(√e)) −ln(2) −(e/2) +(√e) −(1/2) −ln(1+(√e)) +ln(2) I =(e−1)ln(1+(√e)) +(√e) −(e/2) −(1/2) .](Q32753.png)
| ||
Question and Answers Forum | ||
Question Number 32301 by abdo imad last updated on 22/Mar/18 | ||
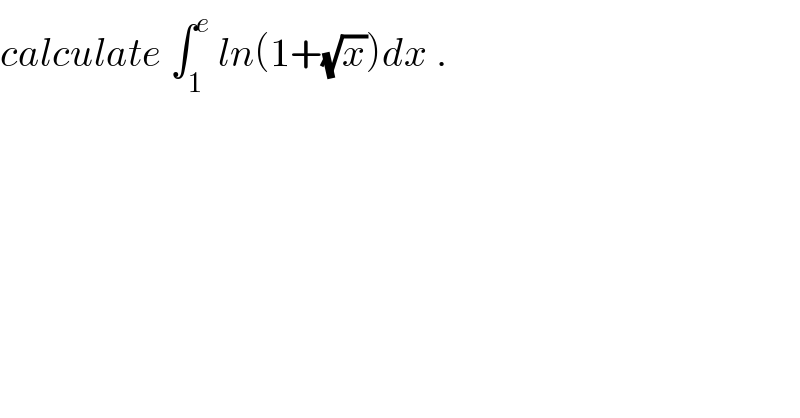 | ||
Commented by abdo imad last updated on 01/Apr/18 | ||
![ch. (√x) =t give I = ∫_1 ^(√e) (2t) ln(1+t)dt .by parts I =( [ t^2 ln(1+t)]_1 ^(√e) − ∫_1 ^(√e) (t^2 /(1+t))dt) =( e ln(1+(√e)) −ln(2) ) − ∫_1 ^(√e) ((t^2 −1+1)/(1+t))dt ∫_1 ^(√e) ((t^2 −1+1)/(1+t)) dt = ∫_1 ^(√e) (t−1) dt +∫_1 ^(√e) (dt/(1+t)) =[(t^2 /2) −t]_1 ^(√e) +[ln(1+t)]_1 ^(√e) =(e/2) −(√e) −(1/2) +1 +ln(1+(√e)) −ln(2) =(e/2) −(√e) +(1/2) +ln(1+(√e)) −ln(2) I =e ln(1+(√e)) −ln(2) −(e/2) +(√e) −(1/2) −ln(1+(√e)) +ln(2) I =(e−1)ln(1+(√e)) +(√e) −(e/2) −(1/2) .](Q32753.png) | ||