Question and Answers Forum
Question Number 36056 by abdo mathsup 649 cc last updated on 28/May/18
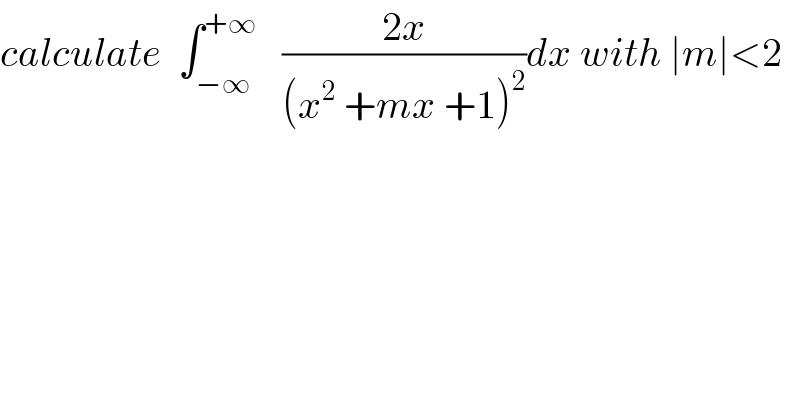
Commented by abdo mathsup 649 cc last updated on 30/May/18
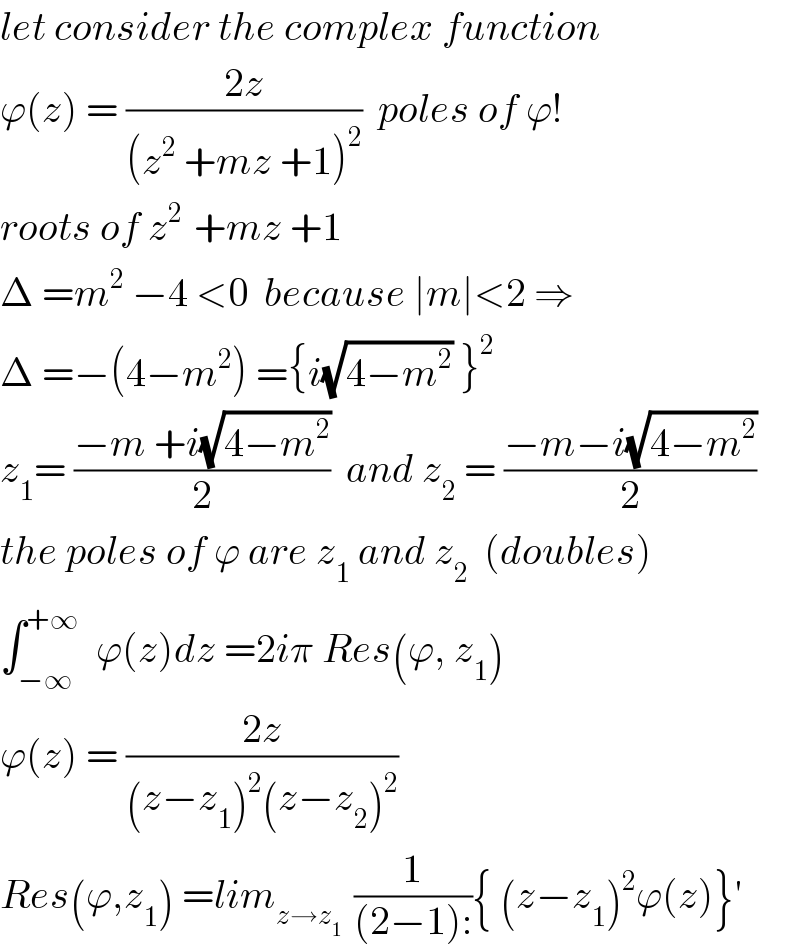
Commented by abdo mathsup 649 cc last updated on 30/May/18
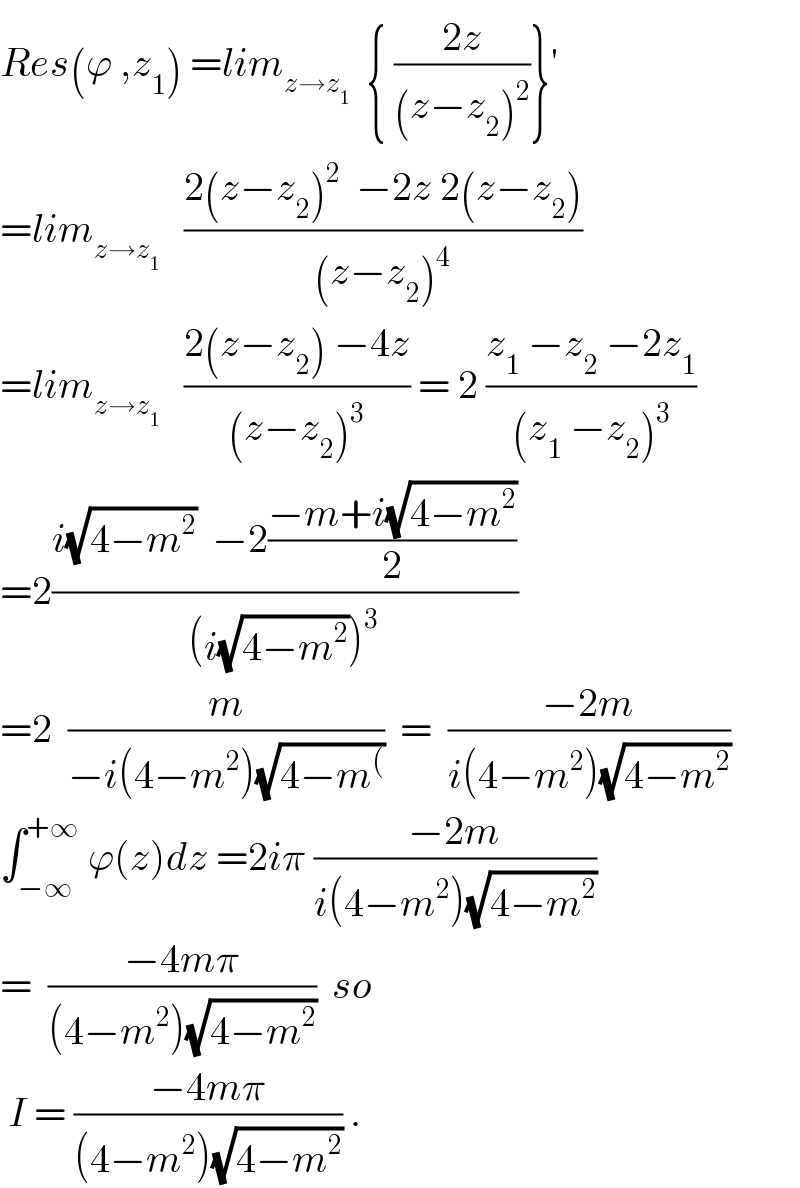
Answered by sma3l2996 last updated on 28/May/18
![I=∫_(−∞) ^(+∞) ((2x)/((x^2 +mx+1)^2 ))dx=∫_(−∞) ^(+∞) ((2x+m−m)/((x^2 +mx+1)^2 ))dx =−[(1/(x^2 +mx+1))]_(−∞) ^(+∞) −m∫_(−∞) ^(+∞) (dx/((x^2 +2×(m/2)×x+(m^2 /4)−(m^2 /4)+1)^2 )) =0−m∫_(−∞) ^(+∞) (dx/(((x+(m/2))^2 +((4−m^2 )/4))^2 )) =−m∫_(−∞) ^(+∞) (dx/((((4−m^2 )/4)((((2x+m)/(√(4−m^2 ))))^2 +1))^2 )) / ∣m∣<2 let u=((2x+m)/(√(4−m^2 )))⇒dx=((√(4−m^2 ))/2)du I=−((8m(√(4−m^2 )))/((4−m^2 )^2 ))∫_(−∞) ^(+∞) (du/((u^2 +1)^2 )) tant=u⇒dt=(du/(1+u^2 )) (du/((u^2 +1)^2 ))=(dt/(1+tan^2 t))=cos^2 (t)dt=(((1+cos(2t))/2))dt ∫_(−π/2) ^(π/2) (1+cos(2t))dt=[t+(1/2)sin2t]_(−π/2) ^(π/2) =π I=−((4πm(√(4−m^2 )))/((4−m^2 )^2 ))](Q36078.png)
Commented by abdo mathsup 649 cc last updated on 30/May/18