
Question and Answers Forum
Question Number 66337 by mathmax by abdo last updated on 12/Aug/19
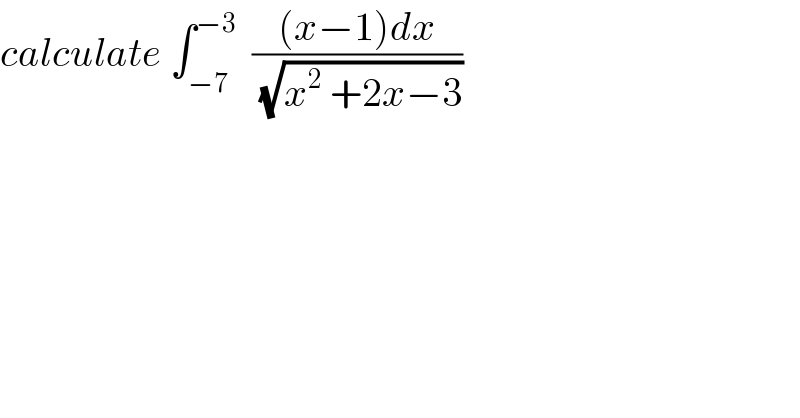
Commented by Prithwish sen last updated on 13/Aug/19
![lim_(ε→−3) ∫_(−7) ^ε ((√(x−1))/(√(x+3))) dx = lim_(ε→−3) [(√((x−1)(x+3) ))−4ln∣(√(x+3))+(√(x−1))∣]_(−7) ^ε =4ln∣1+(√2)∣−4(√2) please check.](Q66361.png)
Commented by mathmax by abdo last updated on 13/Aug/19
![let I =∫_(−7) ^(−3) ((x−1)/(√(x^2 +2x−3)))dx we have x^2 +2x−3 =x^2 +2x+1−4 =(x+1)^2 −4 =(x+1−2)(x+1+2) =(x−1)(x+3) ⇒ I =∫_(−7) ^(−3) ((x−1)/(√((x−1)(x+3))))dx =∫_(−7) ^(−3) ((x−1)/(√((1−x)(−x−3))))dx =−∫_(−7) ^(−3) (((√(1−x)))^2 )/((√(1−x))(√(−x−3))))dx =−∫_(−7) ^(−3) ((√(1−x))/(√(−x−3))) dx we use the changement (√(−x−3))=t ⇒ −x−3=t^2 ⇒−x =3+t^2 ⇒x =−3−t^2 ⇒ I =−∫_2 ^0 ((√(1+3+t^2 ))/t)(−2t)dt =−2∫_0 ^2 (√(t^2 +4)) dt =_(t=2sh(u)) −2∫_0 ^(ln(1+(√2))) 2ch(t)(2ch(t)dt =−8 ∫_0 ^(ln(1+(√2))) ((ch(2t)−1)/2)dt =−4 ∫_0 ^(ln(1+(√2))) (ch(2t)−1)dt=4ln(1+(√2))−4[(1/2)sh(2t)]_0 ^(ln(1+(√2))) =4ln(1+(√2))−2[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(1+(√2))) ⇒ I =4ln(1+(√2))−{(1+(√2))^2 −(1/((1+(√2))^2 ))}](Q66378.png)
| ||
Question and Answers Forum | ||
Question Number 66337 by mathmax by abdo last updated on 12/Aug/19 | ||
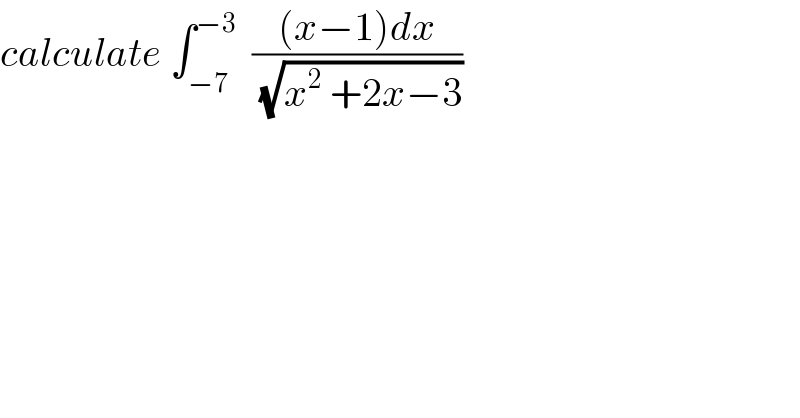 | ||
Commented by Prithwish sen last updated on 13/Aug/19 | ||
![lim_(ε→−3) ∫_(−7) ^ε ((√(x−1))/(√(x+3))) dx = lim_(ε→−3) [(√((x−1)(x+3) ))−4ln∣(√(x+3))+(√(x−1))∣]_(−7) ^ε =4ln∣1+(√2)∣−4(√2) please check.](Q66361.png) | ||
Commented by mathmax by abdo last updated on 13/Aug/19 | ||
![let I =∫_(−7) ^(−3) ((x−1)/(√(x^2 +2x−3)))dx we have x^2 +2x−3 =x^2 +2x+1−4 =(x+1)^2 −4 =(x+1−2)(x+1+2) =(x−1)(x+3) ⇒ I =∫_(−7) ^(−3) ((x−1)/(√((x−1)(x+3))))dx =∫_(−7) ^(−3) ((x−1)/(√((1−x)(−x−3))))dx =−∫_(−7) ^(−3) (((√(1−x)))^2 )/((√(1−x))(√(−x−3))))dx =−∫_(−7) ^(−3) ((√(1−x))/(√(−x−3))) dx we use the changement (√(−x−3))=t ⇒ −x−3=t^2 ⇒−x =3+t^2 ⇒x =−3−t^2 ⇒ I =−∫_2 ^0 ((√(1+3+t^2 ))/t)(−2t)dt =−2∫_0 ^2 (√(t^2 +4)) dt =_(t=2sh(u)) −2∫_0 ^(ln(1+(√2))) 2ch(t)(2ch(t)dt =−8 ∫_0 ^(ln(1+(√2))) ((ch(2t)−1)/2)dt =−4 ∫_0 ^(ln(1+(√2))) (ch(2t)−1)dt=4ln(1+(√2))−4[(1/2)sh(2t)]_0 ^(ln(1+(√2))) =4ln(1+(√2))−2[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(1+(√2))) ⇒ I =4ln(1+(√2))−{(1+(√2))^2 −(1/((1+(√2))^2 ))}](Q66378.png) | ||