
Question and Answers Forum
Question Number 50421 by Abdo msup. last updated on 16/Dec/18
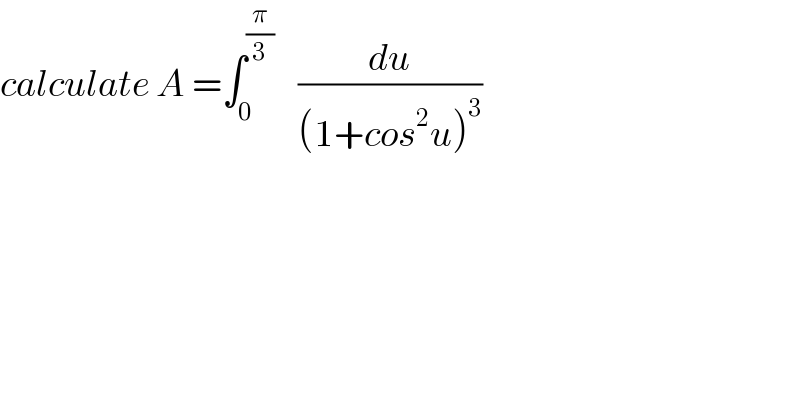
Commented by maxmathsup by imad last updated on 18/Dec/18
![we have 1+cos^2 u =1+(1/(1+tan^2 u)) =((2+tan^2 u)/(1+tan^2 u)) ⇒ A =∫_0 ^(π/3) (du/((((2+tan^2 u)/(1+tan^2 u)))^3 )) =∫_0 ^(π/3) (((1+tan^2 u)^3 )/((2+tan^2 u)^3 )) changement tan(u)=x give A =∫_0 ^(√3) (((1+x^2 )^3 )/((2+x^2 )^3 )) (dx/((1+x^2 ))) =∫_0 ^(√3) ((x^4 +2x^2 +1)/((x^2 +2)^3 )) dx let decompose F(x) =((x^4 +2x^2 +1)/((x^2 +2)^3 )) F(x)=G(u) =((u^2 +2u +1)/((u+2)^3 )) =(a/(u+2)) +(b/((u+2)^2 )) +(c/((u+2)^3 )) c =lim_(u→−2) (u+2)^2 G(u) =1 lim_(u→+∞) uG(u) =1 =a ⇒G(u) =(1/(u+2)) +(b/((u+2)^2 )) +(1/((u+2)^3 )) G(−1) =0 =1 +b +1 =b+2 ⇒b =−2 ⇒G(u)=(1/(u+2)) −(2/((u+2)^2 )) +(1/((u+2)^3 )) ⇒ F(x) = (1/(x^2 +2)) −(2/((x^2 +2)^2 )) +(1/((x^2 +2)^3 )) ⇒ ∫_0 ^(√3) F(x)dx =∫_0 ^(√3) (dx/(x^2 +2)) −2 ∫_0 ^(√3) (dx/((x^2 +2)^2 )) +∫_0 ^(√3) (dx/((x^2 +2)^3 )) ∫_0 ^(√3) (dx/(x^2 +2)) =_(x=(√2)u) ∫_0 ^((√3)/(√2)) (((√2)du)/(2(1+u^2 ))) =(1/(√2)) arctan(((√3)/(√2))). ∫_0 ^(√3) (dx/((x^2 +2)^2 )) =_(x=(√2)tanθ) ∫_0 ^(arctan(((√3)/(√2)))) (((√2)(1+tan^2 θ)dθ)/(4(1+tan^2 θ)^2 )) =((√2)/4)∫_0 ^(arctan(((√3)/(√2)))) cos^2 θ dθ =((√2)/4) ∫_0 ^(arctan(((√3)/(√2)))) ((1+cos(2θ))/2) dθ =((√2)/8) arctan(((√3)/(√2))) +((√2)/(16)) [sin(2θ)]_0 ^(arctan(((√3)/(√2)))) =((√2)/8) arctan(((√3)/(√2))) +((√2)/(16)) sin(2arctan(((√3)/(√2)))). ...be continued...](Q50686.png)
| ||
Question and Answers Forum | ||
Question Number 50421 by Abdo msup. last updated on 16/Dec/18 | ||
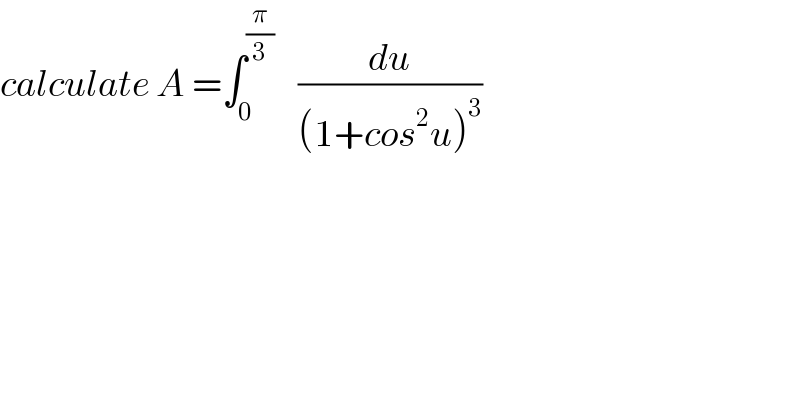 | ||
Commented by maxmathsup by imad last updated on 18/Dec/18 | ||
![we have 1+cos^2 u =1+(1/(1+tan^2 u)) =((2+tan^2 u)/(1+tan^2 u)) ⇒ A =∫_0 ^(π/3) (du/((((2+tan^2 u)/(1+tan^2 u)))^3 )) =∫_0 ^(π/3) (((1+tan^2 u)^3 )/((2+tan^2 u)^3 )) changement tan(u)=x give A =∫_0 ^(√3) (((1+x^2 )^3 )/((2+x^2 )^3 )) (dx/((1+x^2 ))) =∫_0 ^(√3) ((x^4 +2x^2 +1)/((x^2 +2)^3 )) dx let decompose F(x) =((x^4 +2x^2 +1)/((x^2 +2)^3 )) F(x)=G(u) =((u^2 +2u +1)/((u+2)^3 )) =(a/(u+2)) +(b/((u+2)^2 )) +(c/((u+2)^3 )) c =lim_(u→−2) (u+2)^2 G(u) =1 lim_(u→+∞) uG(u) =1 =a ⇒G(u) =(1/(u+2)) +(b/((u+2)^2 )) +(1/((u+2)^3 )) G(−1) =0 =1 +b +1 =b+2 ⇒b =−2 ⇒G(u)=(1/(u+2)) −(2/((u+2)^2 )) +(1/((u+2)^3 )) ⇒ F(x) = (1/(x^2 +2)) −(2/((x^2 +2)^2 )) +(1/((x^2 +2)^3 )) ⇒ ∫_0 ^(√3) F(x)dx =∫_0 ^(√3) (dx/(x^2 +2)) −2 ∫_0 ^(√3) (dx/((x^2 +2)^2 )) +∫_0 ^(√3) (dx/((x^2 +2)^3 )) ∫_0 ^(√3) (dx/(x^2 +2)) =_(x=(√2)u) ∫_0 ^((√3)/(√2)) (((√2)du)/(2(1+u^2 ))) =(1/(√2)) arctan(((√3)/(√2))). ∫_0 ^(√3) (dx/((x^2 +2)^2 )) =_(x=(√2)tanθ) ∫_0 ^(arctan(((√3)/(√2)))) (((√2)(1+tan^2 θ)dθ)/(4(1+tan^2 θ)^2 )) =((√2)/4)∫_0 ^(arctan(((√3)/(√2)))) cos^2 θ dθ =((√2)/4) ∫_0 ^(arctan(((√3)/(√2)))) ((1+cos(2θ))/2) dθ =((√2)/8) arctan(((√3)/(√2))) +((√2)/(16)) [sin(2θ)]_0 ^(arctan(((√3)/(√2)))) =((√2)/8) arctan(((√3)/(√2))) +((√2)/(16)) sin(2arctan(((√3)/(√2)))). ...be continued...](Q50686.png) | ||