
Question and Answers Forum
Question Number 39389 by maxmathsup by imad last updated on 05/Jul/18
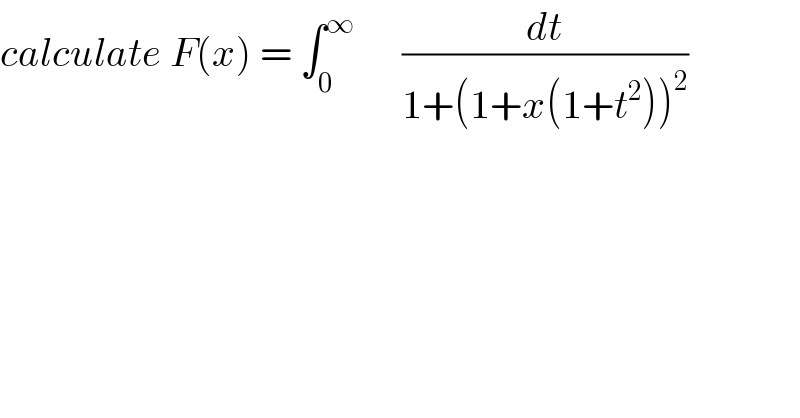
Commented by prof Abdo imad last updated on 24/Jul/18
![changement t=tanθ give F(x) = ∫_0 ^(π/2) (((1+tan^2 θ))/(1+{1+x(1+tan^2 θ)}^2 ))dθ = ∫_0 ^(π/2) (1/(cos^2 θ{1+(x/(cos^2 θ))}^2 ))dθ = ∫_0 ^(π/2) ((cos^2 θ)/({x +cos^2 θ}^2 ))dθ =∫_0 ^(π/2) ((x+cos^2 θ−x)/((x+cos^2 θ)^2 ))dθ = ∫_0 ^(π/2) (dθ/(x +cos^2 θ)) −x ∫_0 ^(π/2) (dθ/((x+cos^2 θ)^2 )) but ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) = ∫_0 ^(π/2) (dθ/(x+((1+cos(2θ))/2))) = ∫_0 ^(π/2) ((2dθ)/(2x+1+cos(2θ))) =_(2θ=t) ∫_0 ^π (dt/(2x+1+cos(t))) =_(u=tan((t/2))) ∫_0 ^∞ (1/(2x+1 +((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫_0 ^∞ ((2du)/((2x+1)u^2 +1−u^2 )) = ∫_0 ^∞ ((2du)/(2xu^2 +1)) if x>0 ∫_0 ^∞ ((2du)/(1+2xu^2 )) =_((√(2x))u=α) ∫_0 ^∞ (2/(1+α^2 )) (dα/(√(2x))) =((√2)/(√x)) .(π/2) if x<0 ∫_0 ^∞ ((2du)/(1+2xu^2 )) = ∫_0 ^∞ ((2du)/(1−((√(−2x))u)^2 )) =∫_0 ^∞ ((2du)/((1−(√(2x))u)(1+(√(2x))u))) = ∫_0 ^∞ { (1/(1−(√(2x))u)) +(1/(1+(√(2x))u))}du =[ln∣((1+(√(2x))u)/(1−(√(2x))u))∣]_0 ^(+∞) =0 so ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) =((π(√2))/(√(2x))) if x>0 ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) =0 if x<0](Q40588.png)
Commented by prof Abdo imad last updated on 24/Jul/18
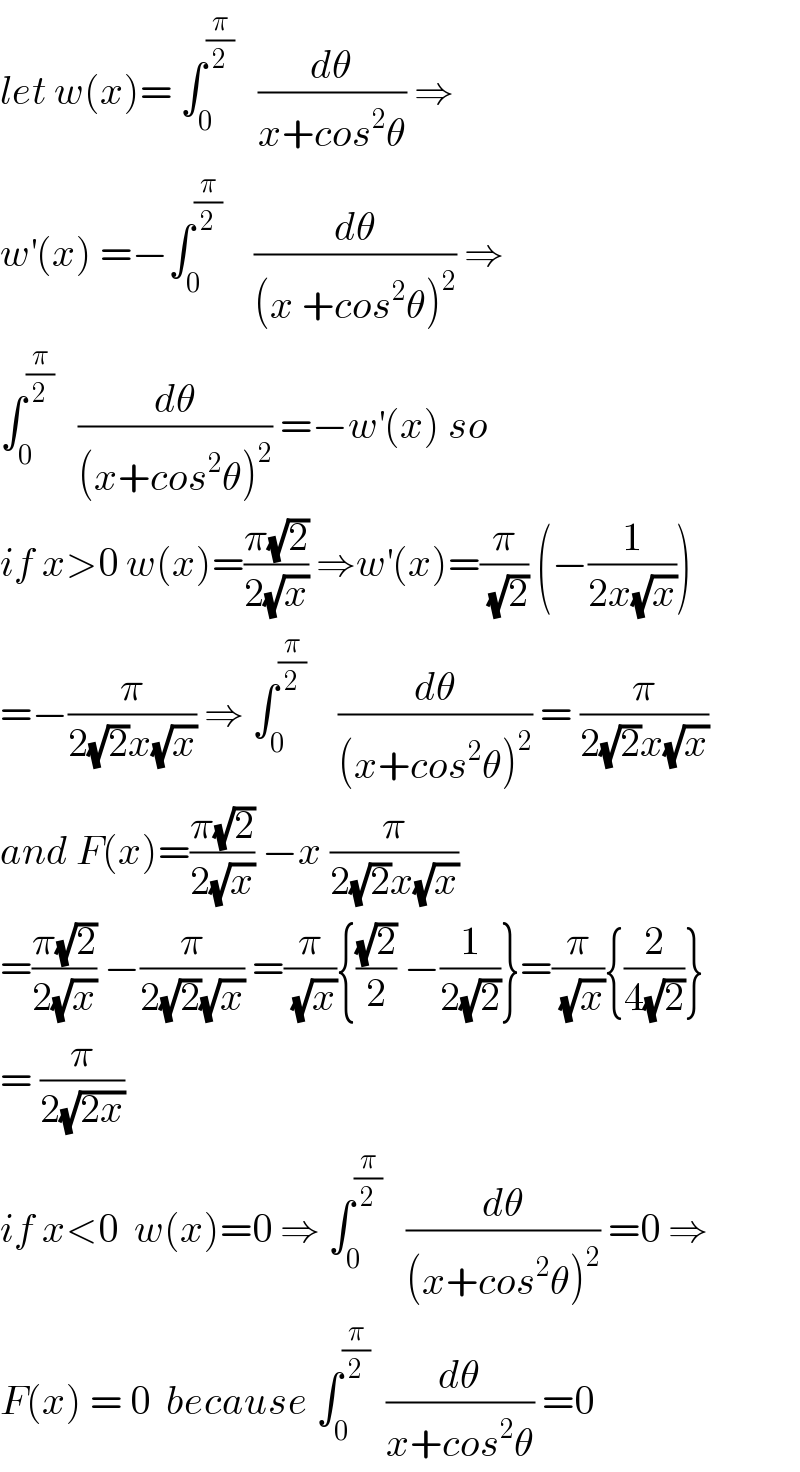
| ||
Question and Answers Forum | ||
Question Number 39389 by maxmathsup by imad last updated on 05/Jul/18 | ||
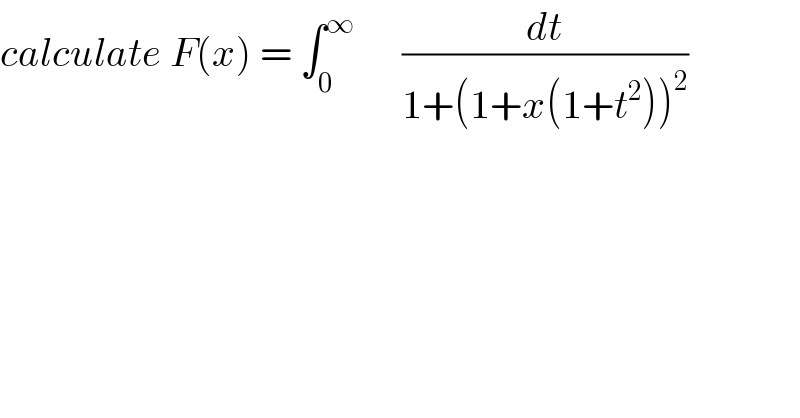 | ||
Commented by prof Abdo imad last updated on 24/Jul/18 | ||
![changement t=tanθ give F(x) = ∫_0 ^(π/2) (((1+tan^2 θ))/(1+{1+x(1+tan^2 θ)}^2 ))dθ = ∫_0 ^(π/2) (1/(cos^2 θ{1+(x/(cos^2 θ))}^2 ))dθ = ∫_0 ^(π/2) ((cos^2 θ)/({x +cos^2 θ}^2 ))dθ =∫_0 ^(π/2) ((x+cos^2 θ−x)/((x+cos^2 θ)^2 ))dθ = ∫_0 ^(π/2) (dθ/(x +cos^2 θ)) −x ∫_0 ^(π/2) (dθ/((x+cos^2 θ)^2 )) but ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) = ∫_0 ^(π/2) (dθ/(x+((1+cos(2θ))/2))) = ∫_0 ^(π/2) ((2dθ)/(2x+1+cos(2θ))) =_(2θ=t) ∫_0 ^π (dt/(2x+1+cos(t))) =_(u=tan((t/2))) ∫_0 ^∞ (1/(2x+1 +((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫_0 ^∞ ((2du)/((2x+1)u^2 +1−u^2 )) = ∫_0 ^∞ ((2du)/(2xu^2 +1)) if x>0 ∫_0 ^∞ ((2du)/(1+2xu^2 )) =_((√(2x))u=α) ∫_0 ^∞ (2/(1+α^2 )) (dα/(√(2x))) =((√2)/(√x)) .(π/2) if x<0 ∫_0 ^∞ ((2du)/(1+2xu^2 )) = ∫_0 ^∞ ((2du)/(1−((√(−2x))u)^2 )) =∫_0 ^∞ ((2du)/((1−(√(2x))u)(1+(√(2x))u))) = ∫_0 ^∞ { (1/(1−(√(2x))u)) +(1/(1+(√(2x))u))}du =[ln∣((1+(√(2x))u)/(1−(√(2x))u))∣]_0 ^(+∞) =0 so ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) =((π(√2))/(√(2x))) if x>0 ∫_0 ^(π/2) (dθ/(x+cos^2 θ)) =0 if x<0](Q40588.png) | ||
Commented by prof Abdo imad last updated on 24/Jul/18 | ||
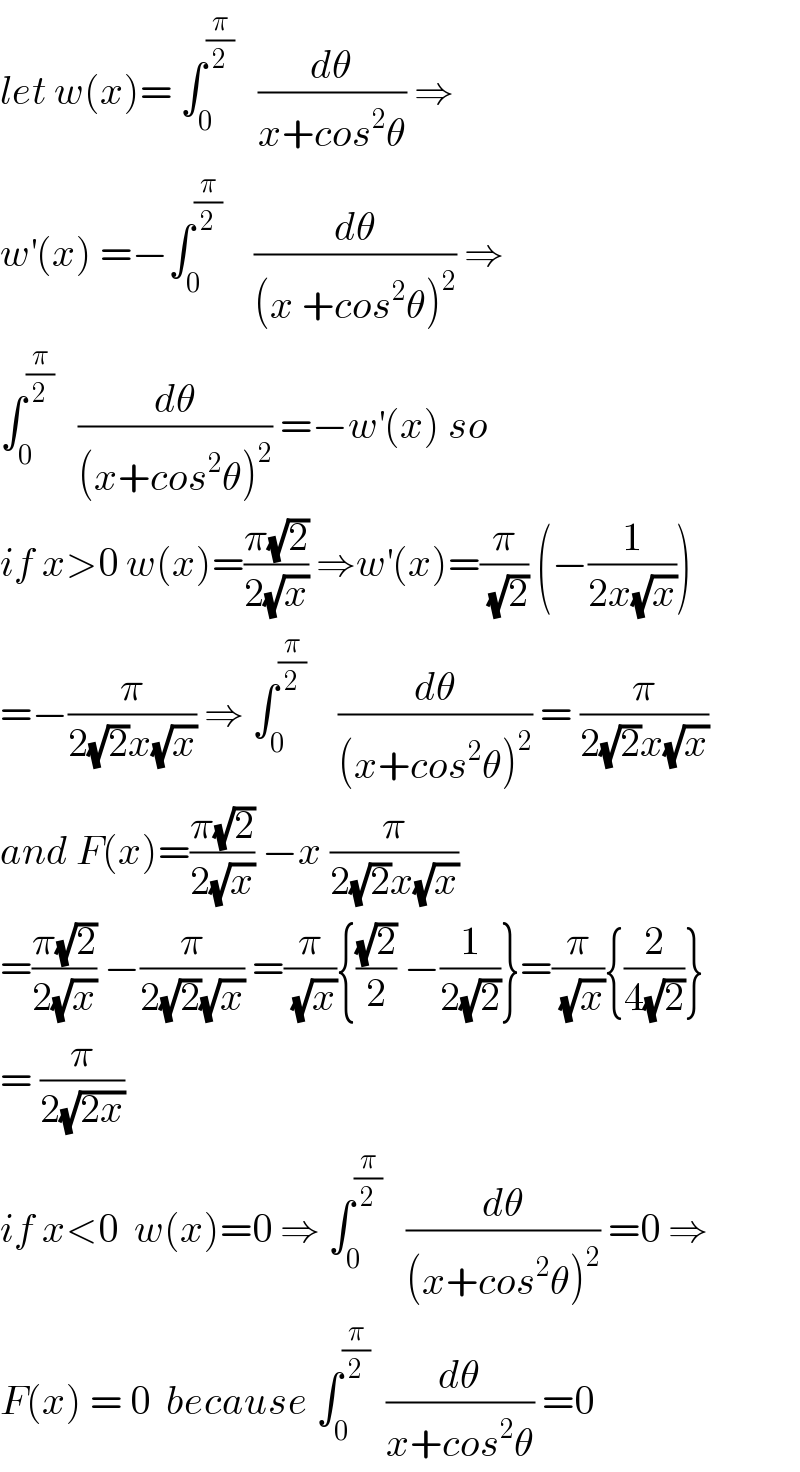 | ||