calculate S(x) = Σ_(n=0) ^∞ (x^(3n) /(3n+1)) after finding the radius of convergence . 2) find the value of Σ


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 35621 by abdo mathsup 649 cc last updated on 21/May/18

$c a l c u l a t e S (x) = \sum_{n = 0}^{\infty} \frac{x^{3 n}}{3 n + 1} a f t e r f i n d i n g$ $t h e r a d i u s o f c o n v e r g e n c e .$ $2) f i n d t h e v a l u e o f \sum_{n = 0}^{\infty} \frac{1}{(3 n + 1) 8^{n}}$
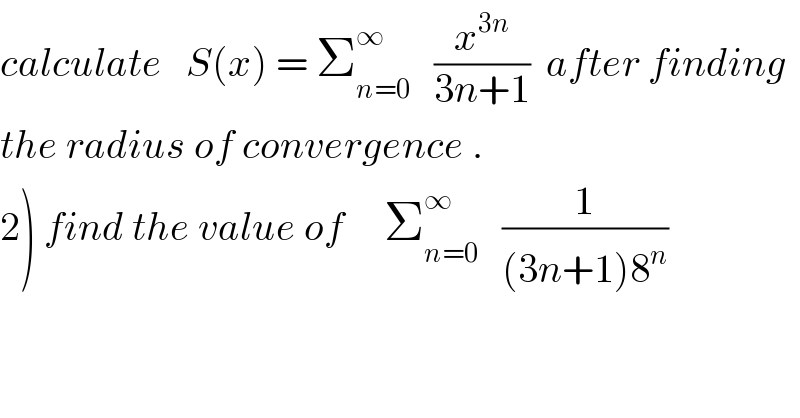
Commented by abdo.msup.com last updated on 25/May/18
$1) let u_n (x)= (x^(3n) /(3n+1)) if x≠0 ∣((u_(n+1) (x))/(u_n (x)))∣ = ∣ ((x^(3n+3) /(3n+4))/(x^(3n) /(3n+1)))∣ =((3n+1)/(3n+4)) ∣x∣^3 →∣x∣^3 so if ∣x∣<1 the serie converged so R =1 let find S(x) we have x S(x) = Σ_(n=0) ^∞ (x^(3n+1) /(3n+1)) =w(x) w^′ (x)= Σ_(n=0) ^∞ x^(3n) = (1/(1−x^3 )) ⇒ w(x) = ∫_0 ^x (dt/(1−t^3 )) +c but c=w(0)=0 F(t) = (1/(1−t^3 )) = (1/((1−t)(t^2 +t +1))) =(a/(1−t)) +((bt +c)/(t^2 +t +1)) a=lim_(t→1) (1−t)F(t) =(1/3) F(t) = (1/(3(1−t))) +((bt +c)/(t^2 +t +1)) lim_(t→+∞) t F(t) = −(1/3) +b =0⇒b=(1/3) F(t) = (1/(3(1−t))) +(((1/3)t +c)/(t^2 +t+1)) F(0) = (1/3) +c =1⇒c=1−(1/3) =(2/3) so F(t)= (1/(3(1−t))) +(1/3) ((t+2)/(t^2 +t+1)) 3w(x)=∫_0 ^x (dt/(1−t)) + (1/2)∫_0 ^x ((2t+1+3)/(t^2 +t+1))dt =[−ln∣1−t∣]_0 ^x +(1/2)[ln(t^2 +t+1)]_0 ^x +(3/2) ∫_0 ^x (dt/(t^2 +t+1)) =−ln∣1−x∣ +(1/2)ln(x^(2 ) +x+1)+(3/2) I I = ∫_0 ^x (dt/((t+(1/2))^2 +(3/4))) =_(t +(1/2)=((√3)/2) u) ∫_(1/(√3)) ^((2x+1)/(√3)) (1/((3/4)( 1+u^2 )))((√3)/2)du = (4/3) ((√3)/2) [arctan(u)]_(1/(√3)) ^((2x+1)/(√3)) = (2/(√3)) { arctan(((2x+1)/(√3))) −arctan((1/(√3)))} 3w(x)=−ln∣1−x∣ +(1/2)ln(x^2 +x+1) +(√3){arctan(((2x+1)/(√3))) −(π/6)} ⇒ w(x) =−(1/3)ln∣1−x∣ +(1/6)ln(x^2 +x+1) + (1/(√3)){ arctan(((2x+1)/(√3))) −(π/6)}and S(x)= ((w(x))/x)$
$1) l e t u_{n} (x) = \frac{x^{3 n}}{3 n + 1} i f x \neq 0$ $∣ \frac{u_{n + 1} (x)}{u_{n} (x)} ∣ = ∣ \frac{\frac{x^{3 n + 3}}{3 n + 4}}{\frac{x^{3 n}}{3 n + 1}} ∣ = \frac{3 n + 1}{3 n + 4} ∣ x ∣^{3}$ $\to∣ x ∣^{3} s o i f ∣ x ∣< 1 t h e s e r i e c o n v e r g e d$ $s o R = 1 l e t f i n d S (x)$ $w e h a v e x S (x) = \sum_{n = 0}^{\infty} \frac{x^{3 n + 1}}{3 n + 1} = w (x)$ $w^{^{'}} (x) = \sum_{n = 0}^{\infty} x^{3 n} = \frac{1}{1 - x^{3}} \Rightarrow$ $w (x) = \int_{0}^{x} \frac{d t}{1 - t^{3}} + c b u t c = w (0) = 0$ $F (t) = \frac{1}{1 - t^{3}} = \frac{1}{(1 - t) (t^{2} + t + 1)}$ $= \frac{a}{1 - t} + \frac{b t + c}{t^{2} + t + 1}$ $a = {l i m}_{t \to 1} (1 - t) F (t) = \frac{1}{3}$ $F (t) = \frac{1}{3 (1 - t)} + \frac{b t + c}{t^{2} + t + 1}$ ${l i m}_{t \to + \infty} t F (t) = - \frac{1}{3} + b = 0 \Rightarrow b = \frac{1}{3}$ $F (t) = \frac{1}{3 (1 - t)} + \frac{\frac{1}{3} t + c}{t^{2} + t + 1}$ $F (0) = \frac{1}{3} + c = 1 \Rightarrow c = 1 - \frac{1}{3} = \frac{2}{3}$ $s o F (t) = \frac{1}{3 (1 - t)} + \frac{1}{3} \frac{t + 2}{t^{2} + t + 1}$ $3 w (x) = \int_{0}^{x} \frac{d t}{1 - t} + \frac{1}{2} \int_{0}^{x} \frac{2 t + 1 + 3}{t^{2} + t + 1} d t$ $= {[- l n ∣ 1 - t ∣]}_{0}^{x} + \frac{1}{2} {[l n (t^{2} + t + 1)]}_{0}^{x}$ $+ \frac{3}{2} \int_{0}^{x} \frac{d t}{t^{2} + t + 1}$ $= - l n ∣ 1 - x ∣ + \frac{1}{2} l n (x^{2} + x + 1) + \frac{3}{2} I$ $I = \int_{0}^{x} \frac{d t}{{(t + \frac{1}{2})}^{2} + \frac{3}{4}}$ $=_{t + \frac{1}{2} = \frac{\sqrt{3}}{2} u} \int_{\frac{1}{\sqrt{3}}}^{\frac{2 x + 1}{\sqrt{3}}} \frac{1}{\frac{3}{4} (1 + u^{2})} \frac{\sqrt{3}}{2} d u$ $= \frac{4}{3} \frac{\sqrt{3}}{2} {[a r c t a n (u)]}_{\frac{1}{\sqrt{3}}}^{\frac{2 x + 1}{\sqrt{3}}}$ $= \frac{2}{\sqrt{3}} {a r c t a n (\frac{2 x + 1}{\sqrt{3}}) - a r c t a n (\frac{1}{\sqrt{3}})}$ $3 w (x) = - l n ∣ 1 - x ∣ + \frac{1}{2} l n (x^{2} + x + 1)$ $+ \sqrt{3} {a r c t a n (\frac{2 x + 1}{\sqrt{3}}) - \frac{π}{6}} \Rightarrow$ $w (x) = - \frac{1}{3} l n ∣ 1 - x ∣ + \frac{1}{6} l n (x^{2} + x + 1)$ $+ \frac{1}{\sqrt{3}} {a r c t a n (\frac{2 x + 1}{\sqrt{3}}) - \frac{π}{6}} a n d$ $S (x) = \frac{w (x)}{x}$
Commented by abdo.msup.com last updated on 25/May/18
$2) Σ_(n=0) ^∞ (1/((3n+1)8^n )) =S((1/2)) =2w((1/2))=2{ −(1/3)ln((1/2))+(1/6)ln((7/4)) +(1/(√3)){ arctan((2/(√3))) −(π/6)} =(2/3)ln(2) + (1/3)ln((7/4)) +(2/(√3))arctan((2/(√3))) −(π/(3(√3))) .$
$2) \sum_{n = 0}^{\infty} \frac{1}{(3 n + 1) 8^{n}} = S (\frac{1}{2})$ $= 2 w (\frac{1}{2}) = 2 {- \frac{1}{3} l n (\frac{1}{2}) + \frac{1}{6} l n (\frac{7}{4})$ $+ \frac{1}{\sqrt{3}} {a r c t a n (\frac{2}{\sqrt{3}}) - \frac{π}{6}}$ $= \frac{2}{3} l n (2) + \frac{1}{3} l n (\frac{7}{4}) + \frac{2}{\sqrt{3}} a r c t a n (\frac{2}{\sqrt{3}})$ $- \frac{π}{3 \sqrt{3}} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum