
Question and Answers Forum
Question Number 143083 by Mathspace last updated on 09/Jun/21
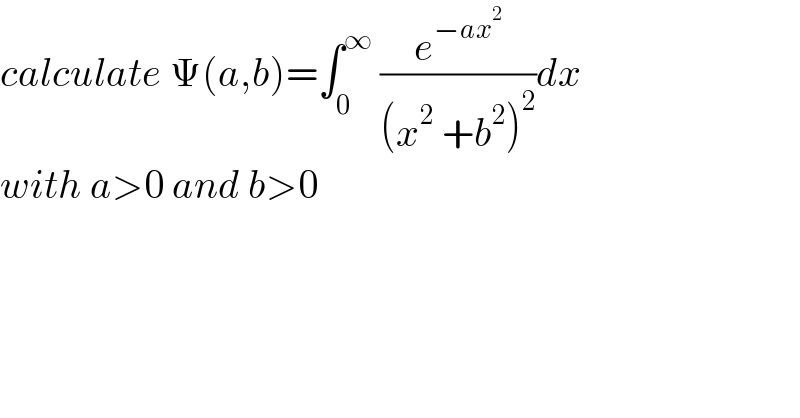
Answered by Olaf_Thorendsen last updated on 10/Jun/21
![f_b (a) = Ψ(a,b) = ∫_0 ^∞ (e^(−ax^2 ) /((x^2 +b^2 )^2 )) dx f_b ′(a) = (∂Ψ/∂a)(a,b) = −∫_0 ^∞ ((x^2 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx f_b ′′(a) = (∂^2 Ψ/∂a^2 )(a,b) = +∫_0 ^∞ ((x^4 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx f_b ′′(a)−2b^2 f_b ′(a)+b^4 f_b (a) = ∫_0 ^∞ (((x^4 +2b^2 x^2 +b^4 )e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx = ∫_0 ^∞ (((x^2 +b^2 )^2 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx = ∫_0 ^∞ e^(−ax^2 ) dx = (1/( (√a)))∫_0 ^∞ e^(−t^2 ) dt =(1/2) (√(π/a))((2/( (√π)))∫_0 ^∞ e^(−t^2 ) dt) =(1/2) (√(π/a)) f_b ′′(a)−2b^2 f_b ′(a)+b^4 f_b (a) = (1/2)(√(π/a)) f_b (a) = Ψ(a,b) = (c_1 +c_2 a)e^(ab^2 ) +((√π)/2)e^(ab^2 ) [aΓ((1/2),b^2 a)+((Γ((3/2),ab^2 ))/b^3 )] ...to be continued...](Q143099.png)
| ||
Question and Answers Forum | ||
Question Number 143083 by Mathspace last updated on 09/Jun/21 | ||
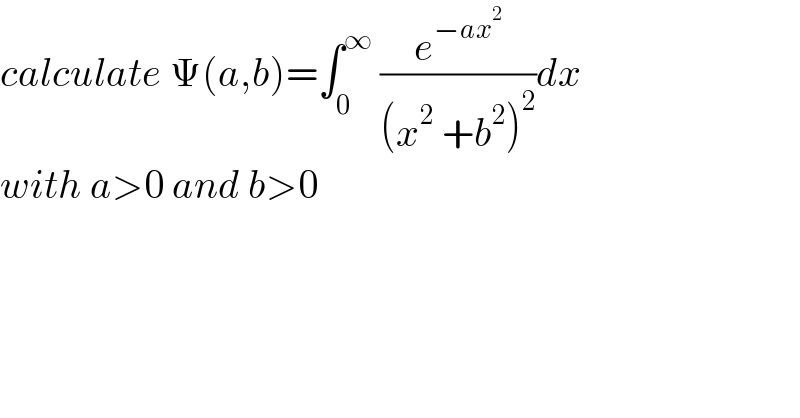 | ||
Answered by Olaf_Thorendsen last updated on 10/Jun/21 | ||
![f_b (a) = Ψ(a,b) = ∫_0 ^∞ (e^(−ax^2 ) /((x^2 +b^2 )^2 )) dx f_b ′(a) = (∂Ψ/∂a)(a,b) = −∫_0 ^∞ ((x^2 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx f_b ′′(a) = (∂^2 Ψ/∂a^2 )(a,b) = +∫_0 ^∞ ((x^4 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx f_b ′′(a)−2b^2 f_b ′(a)+b^4 f_b (a) = ∫_0 ^∞ (((x^4 +2b^2 x^2 +b^4 )e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx = ∫_0 ^∞ (((x^2 +b^2 )^2 e^(−ax^2 ) )/((x^2 +b^2 )^2 )) dx = ∫_0 ^∞ e^(−ax^2 ) dx = (1/( (√a)))∫_0 ^∞ e^(−t^2 ) dt =(1/2) (√(π/a))((2/( (√π)))∫_0 ^∞ e^(−t^2 ) dt) =(1/2) (√(π/a)) f_b ′′(a)−2b^2 f_b ′(a)+b^4 f_b (a) = (1/2)(√(π/a)) f_b (a) = Ψ(a,b) = (c_1 +c_2 a)e^(ab^2 ) +((√π)/2)e^(ab^2 ) [aΓ((1/2),b^2 a)+((Γ((3/2),ab^2 ))/b^3 )] ...to be continued...](Q143099.png) | ||
| ||