
Question and Answers Forum
Question Number 35055 by math khazana by abdo last updated on 14/May/18
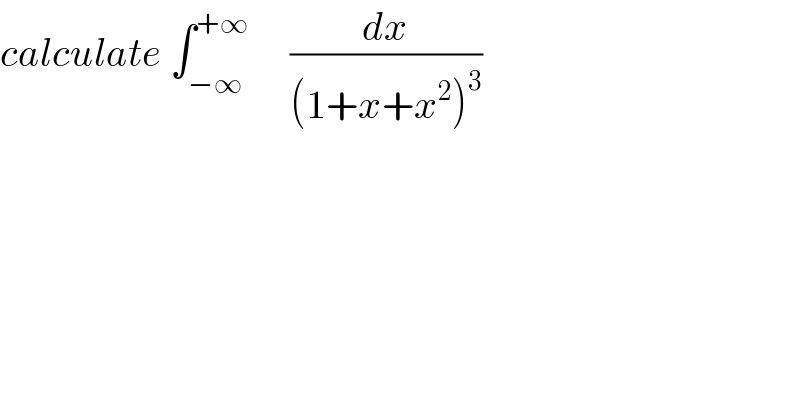
Commented by math khazana by abdo last updated on 15/May/18
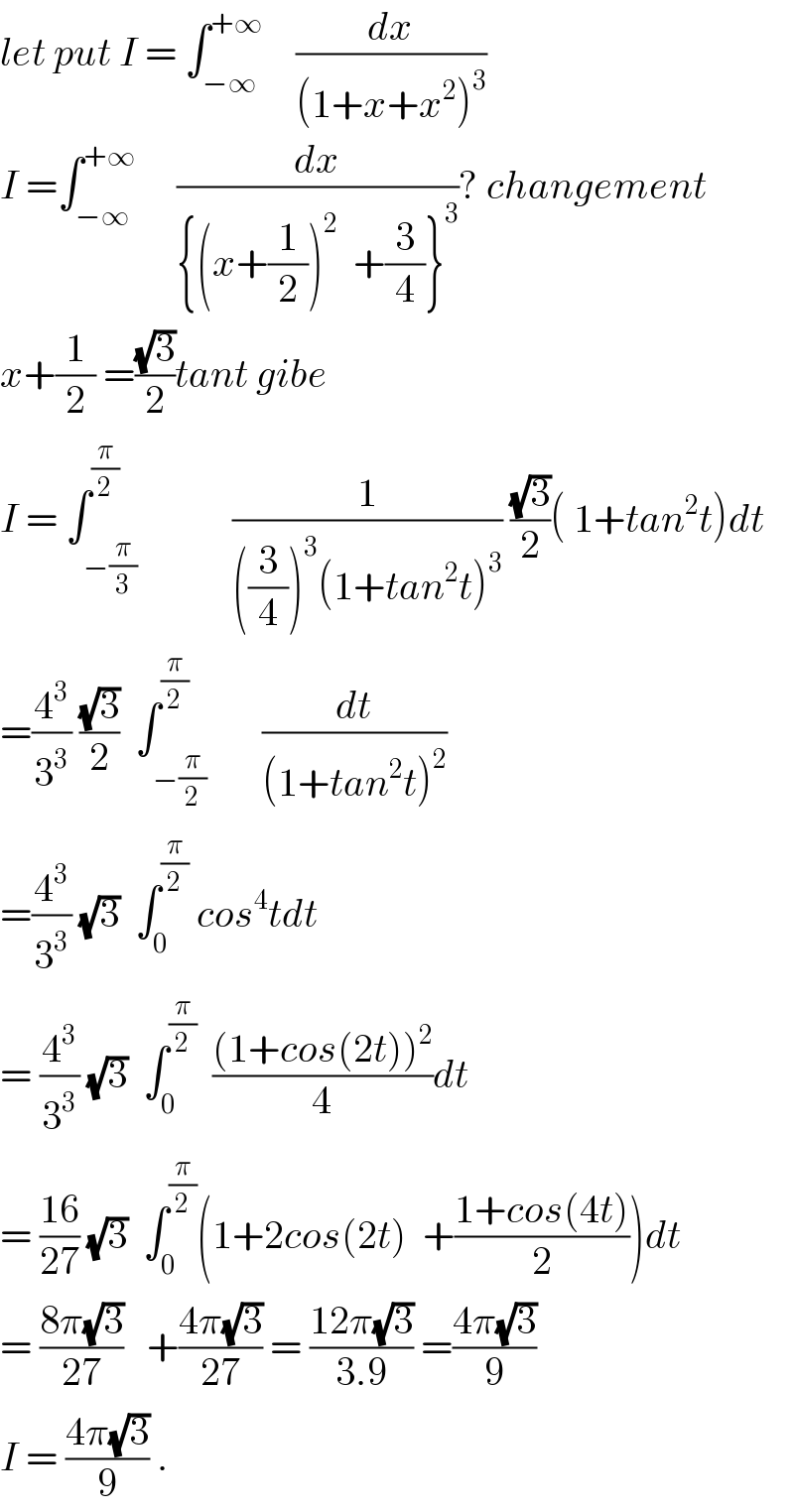
Commented by abdo imad last updated on 17/May/18
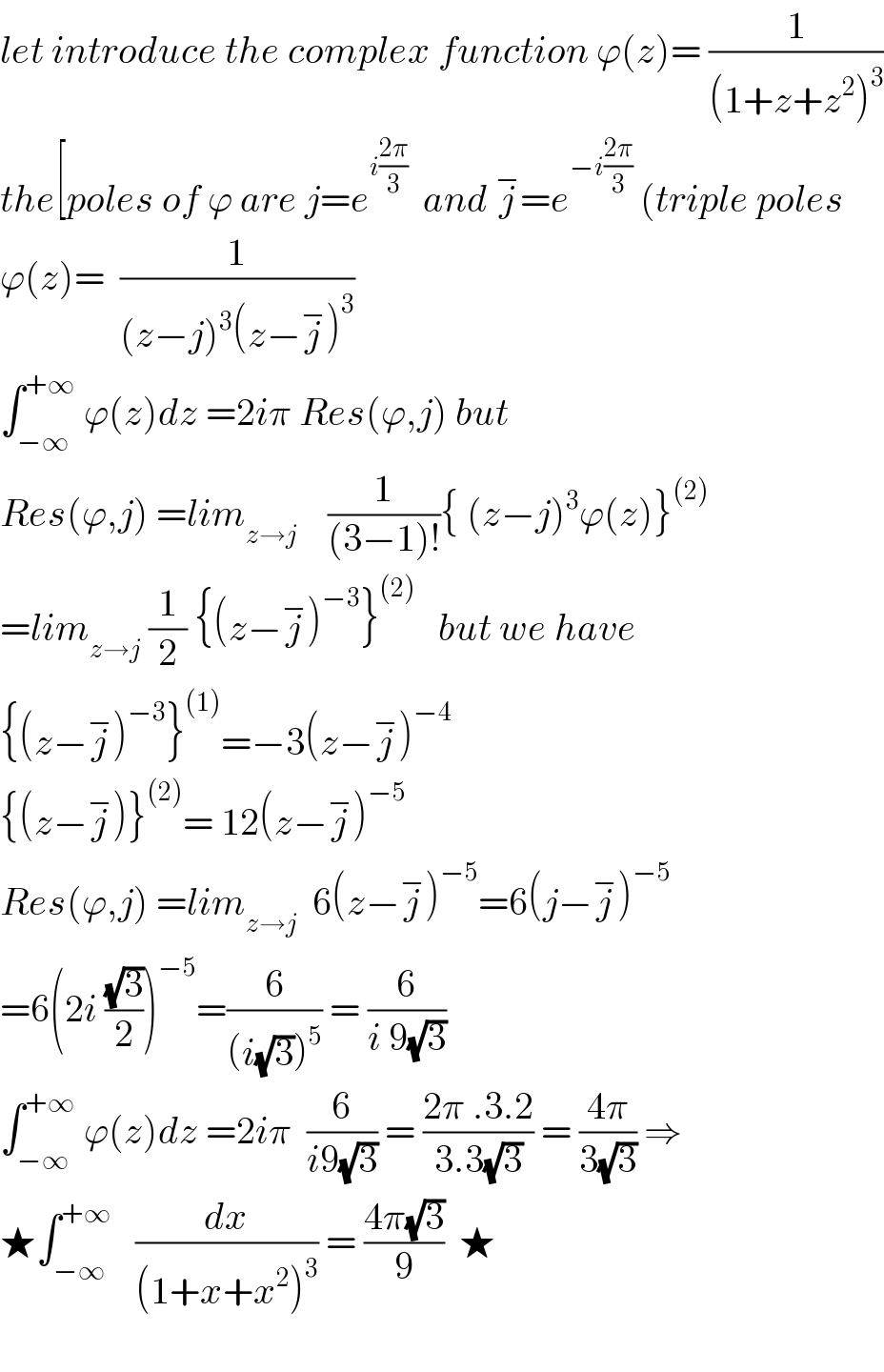
Answered by MJS last updated on 15/May/18
![∫(dx/((x^2 +x+1)^3 ))=∫(dx/(((x+(1/2))^2 +(3/4))^3 ))= =64∫(dx/(((2x+1)^2 ++3)^3 ))= [u=2x+1 → dx=(du/2)] =32∫(du/((u^2 +3)^3 )) [∫(du/((au^2 +b)^n ))=(u/(2b(n−1)(au^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(du/((au^2 +b)^(n−1) ))] a=1; b=3; n=3 =32((u/(12(u^2 +3)^2 ))+(1/4)∫(du/((u^2 +3)^2 )))= a=1; b=3; n=2 =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+(1/6)∫(du/(u^2 +3))))= [v=((u(√3))/3) → du=(√3)dv] =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))∫(dv/(v^2 +1))))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(v)))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(((u(√3))/3))))= =((8u)/(3(u^2 +3)^2 ))+((4u)/(3(u^2 +3)))+((4(√3))/9)arctan(((u(√3))/3))= =((4u(u^2 +5))/(3(u^2 +3)^2 ))+((4(√3))/9)arctan(((u(√3))/3))= =((4(2x+1)((2x+1)^2 +5))/(3((2x+1)^2 +3)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))= =(((2x+1)(2x^2 +2x+3))/(6(x^2 +x+1)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))+C ∫_(−∞) ^∞ (dx/((x^2 +x+1)^3 ))=((4(√3))/9)π](Q35100.png)
| ||
Question and Answers Forum | ||
Question Number 35055 by math khazana by abdo last updated on 14/May/18 | ||
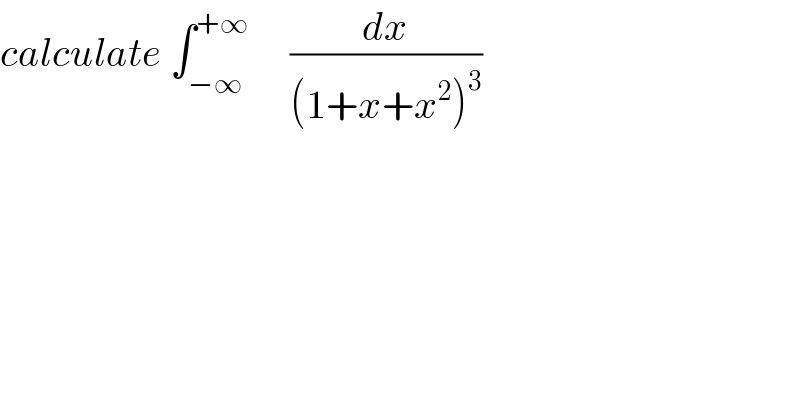 | ||
Commented by math khazana by abdo last updated on 15/May/18 | ||
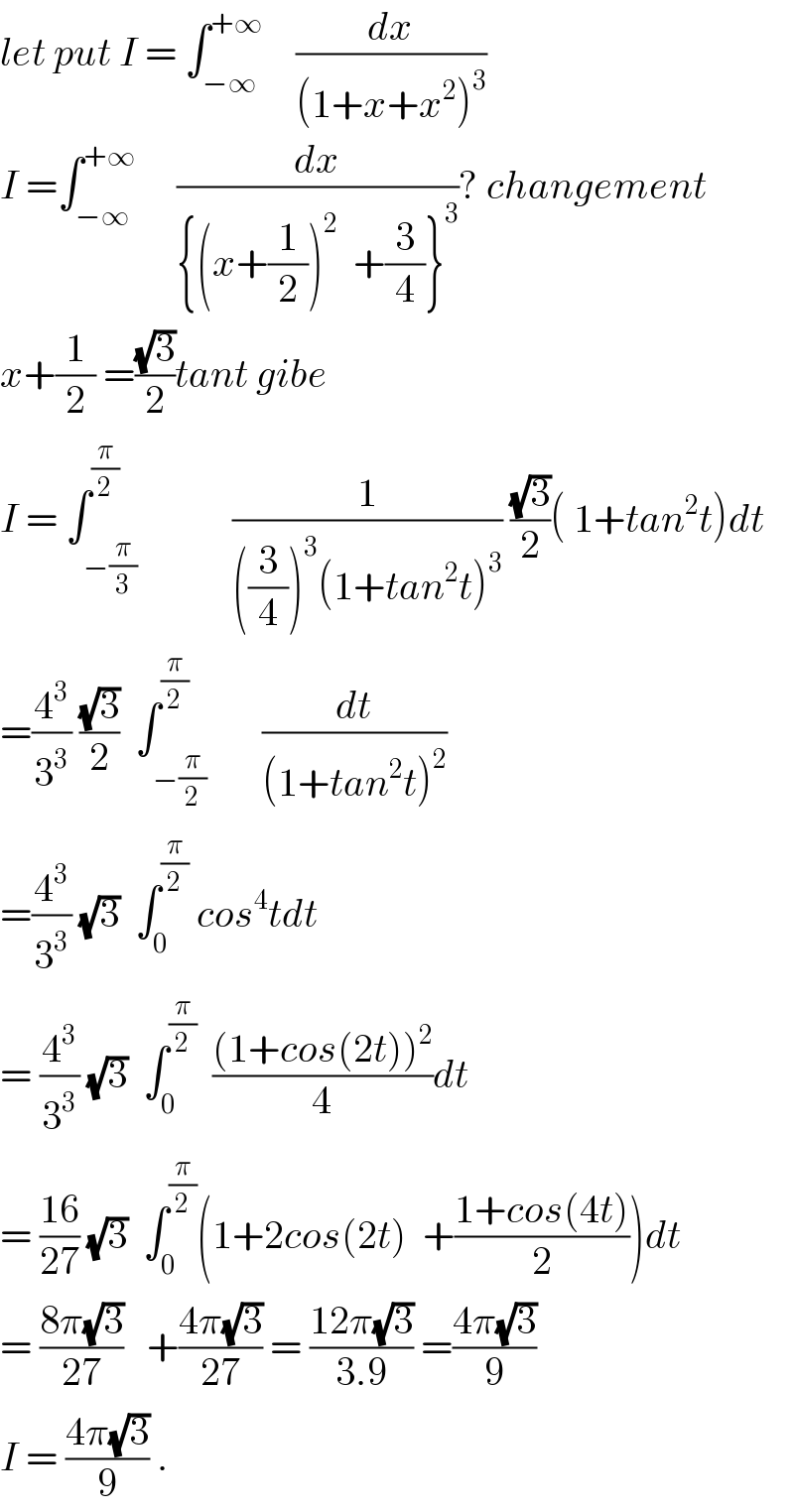 | ||
Commented by abdo imad last updated on 17/May/18 | ||
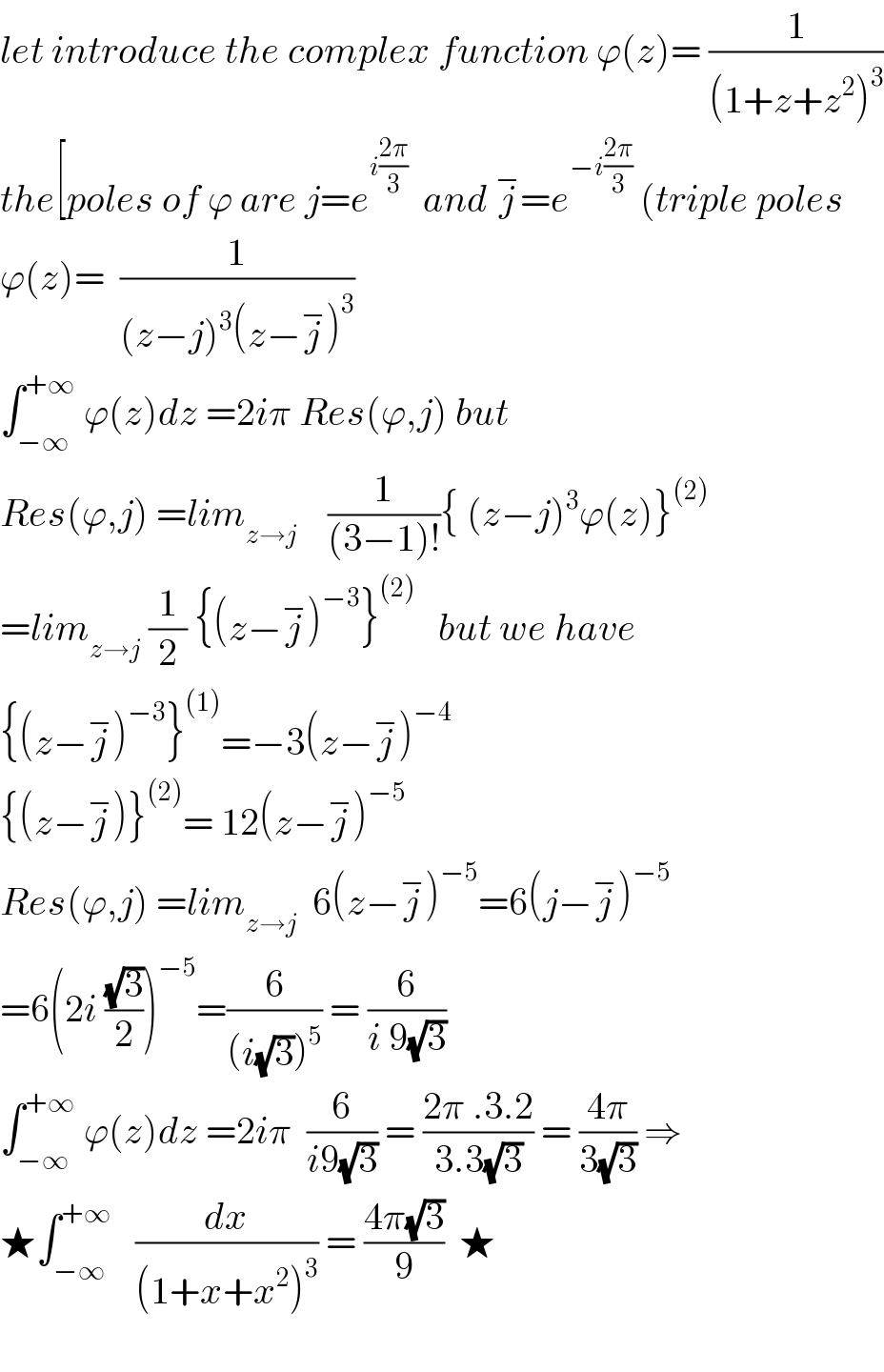 | ||
Answered by MJS last updated on 15/May/18 | ||
![∫(dx/((x^2 +x+1)^3 ))=∫(dx/(((x+(1/2))^2 +(3/4))^3 ))= =64∫(dx/(((2x+1)^2 ++3)^3 ))= [u=2x+1 → dx=(du/2)] =32∫(du/((u^2 +3)^3 )) [∫(du/((au^2 +b)^n ))=(u/(2b(n−1)(au^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(du/((au^2 +b)^(n−1) ))] a=1; b=3; n=3 =32((u/(12(u^2 +3)^2 ))+(1/4)∫(du/((u^2 +3)^2 )))= a=1; b=3; n=2 =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+(1/6)∫(du/(u^2 +3))))= [v=((u(√3))/3) → du=(√3)dv] =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))∫(dv/(v^2 +1))))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(v)))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(((u(√3))/3))))= =((8u)/(3(u^2 +3)^2 ))+((4u)/(3(u^2 +3)))+((4(√3))/9)arctan(((u(√3))/3))= =((4u(u^2 +5))/(3(u^2 +3)^2 ))+((4(√3))/9)arctan(((u(√3))/3))= =((4(2x+1)((2x+1)^2 +5))/(3((2x+1)^2 +3)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))= =(((2x+1)(2x^2 +2x+3))/(6(x^2 +x+1)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))+C ∫_(−∞) ^∞ (dx/((x^2 +x+1)^3 ))=((4(√3))/9)π](Q35100.png) | ||
| ||