calculate ∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +1))


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 67310 by mathmax by abdo last updated on 25/Aug/19

$c a l c u l a t e \int_{- \infty}^{+ \infty} \frac{d x}{x^{4} + x^{2} + 1}$
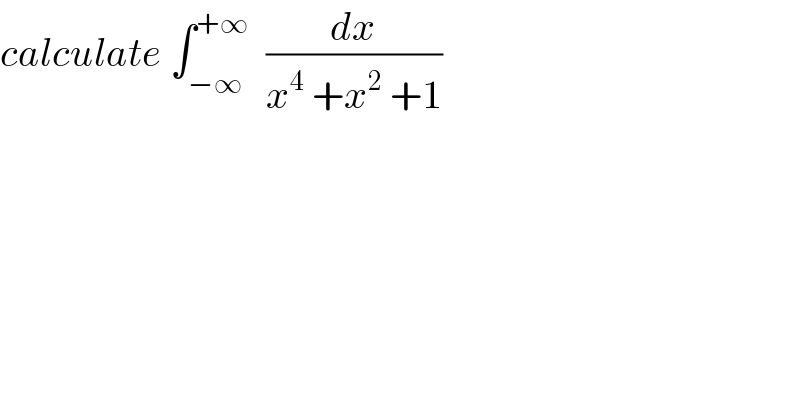
Commented by mathmax by abdo last updated on 25/Aug/19
$let I =∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +1)) ⇒I =2 ∫_0 ^(+∞) (dx/(x^4 +x^2 +1)) we have x^4 +x^2 +1 =(x^2 +1)^2 −2x^2 +x^2 =(x^2 +1)^2 −x^2 =(x^2 −x+1)(x^2 +x+1) ⇒ I =2 ∫_0 ^(+∞) (dx/((x^2 +x+1)(x^2 −x+1))) let decompose F(x) =(1/((x^2 +x+1)(x^2 −x+1))) F(x) =((ax+b)/(x^2 +x +1)) +((cx+d)/(x^2 −x+1)) F(−x)=F(x) ⇒((−ax+b)/(x^2 −x+1)) +((−cx+d)/(x^2 +x+1)) =F(x) ⇒ c=−a and d=b ⇒F(x) =((ax+b)/(x^2 +x+1)) +((−ax+b)/(x^2 −x +1)) F(0) =1 =2b ⇒b =(1/2) F(1) =(1/3) =((a+b)/3) +b−a ⇒3 =a+b+3b−3a =−2a+2 ⇒1 =−2a ⇒ a=−(1/2) ⇒ F(x) =((−(1/2)x+(1/2))/(x^2 +x+1)) +(((1/2)x+(1/2))/(x^2 −x +1)) =(1/2){((−x+1)/(x^2 +x+1))+((x+1)/(x^2 −x +1))} ⇒∫_0 ^(+∞) F(x)dx =−(1/2) ∫_0 ^∞ ((x−1)/(x^2 +x+1))dx +(1/2)∫_0 ^∞ ((x+1)/(x^2 −x+1))dx =−(1/4)∫_0 ^∞ ((2x+1−3)/(x^2 +x+1))dx +(1/4)∫_0 ^∞ ((2x−1+3)/(x^2 −x +1))dx =(1/4)[ln∣((x^2 −x+1)/(x^2 +x+1))∣]_0 ^(+∞) +(3/4)∫_0 ^∞ (dx/(x^2 −x +1)) +(3/4)∫_0 ^∞ (dx/(x^2 +x+1)) =0 +(3/4) ∫_0 ^∞ (dx/(x^2 −x+1)) +(3/4)∫_0 ^∞ (dx/(x^2 +x +1)) ∫_0 ^∞ (dx/(x^2 −x +1)) =∫_0 ^∞ (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3) ∫_(−(1/(√3))) ^(+∞) (1/(u^2 +1))((√3)/2)du =(2/(√3))[arctanu]_(−(1/(√3))) ^(+∞) =(2/(√3)){ (π/2) +arctan((1/(√3)))}=(2/(√3)){(π/2)+(π/6)} =(2/(√3)){((2π)/3)} =((4π)/(3(√3))) ∫_0 ^∞ (dx/(x^2 +x +1)) =∫_0 ^∞ (dx/((x+(1/2))^(2 ) +(3/4))) =_(x+(1/2)=((√3)/2)u) (4/3) ∫_(1/(√3)) ^∞ (1/(u^2 +1))((√3)/2)du =((2(√3))/3)[arctan(u)]_(1/(√3)) ^(+∞) =(2/(√3)){(π/2)−(π/6)}=(2/(√3)){(π/3)} =((2π)/(3(√3))) ⇒ ∫_0 ^∞ F(x)dx =(3/4)×((4π)/(3(√3))) +(3/4)×((2π)/(3(√3))) =(π/(√3)) +(π/(2(√3))) =(3/2)(π/(√3)) we have I =2 ∫_0 ^∞ F(x)dx =((3π)/(√3)) =π(√3)$
$l e t I = \int_{- \infty}^{+ \infty} \frac{d x}{x^{4} + x^{2} + 1} \Rightarrow I = 2 \int_{0}^{+ \infty} \frac{d x}{x^{4} + x^{2} + 1}$ $w e h a v e x^{4} + x^{2} + 1 = {(x^{2} + 1)}^{2} - 2 x^{2} + x^{2} = {(x^{2} + 1)}^{2} - x^{2}$ $= (x^{2} - x + 1) (x^{2} + x + 1) \Rightarrow I = 2 \int_{0}^{+ \infty} \frac{d x}{(x^{2} + x + 1) (x^{2} - x + 1)}$ $l e t d e c o m p o s e F (x) = \frac{1}{(x^{2} + x + 1) (x^{2} - x + 1)}$ $F (x) = \frac{a x + b}{x^{2} + x + 1} + \frac{c x + d}{x^{2} - x + 1}$ $F (- x) = F (x) \Rightarrow \frac{- a x + b}{x^{2} - x + 1} + \frac{- c x + d}{x^{2} + x + 1} = F (x) \Rightarrow$ $c = - a a n d d = b \Rightarrow F (x) = \frac{a x + b}{x^{2} + x + 1} + \frac{- a x + b}{x^{2} - x + 1}$ $F (0) = 1 = 2 b \Rightarrow b = \frac{1}{2}$ $F (1) = \frac{1}{3} = \frac{a + b}{3} + b - a \Rightarrow 3 = a + b + 3 b - 3 a = - 2 a + 2 \Rightarrow 1 = - 2 a \Rightarrow$ $a = - \frac{1}{2} \Rightarrow F (x) = \frac{- \frac{1}{2} x + \frac{1}{2}}{x^{2} + x + 1} + \frac{\frac{1}{2} x + \frac{1}{2}}{x^{2} - x + 1}$ $= \frac{1}{2} {\frac{- x + 1}{x^{2} + x + 1} + \frac{x + 1}{x^{2} - x + 1}} \Rightarrow \int_{0}^{+ \infty} F (x) d x$ $= - \frac{1}{2} \int_{0}^{\infty} \frac{x - 1}{x^{2} + x + 1} d x + \frac{1}{2} \int_{0}^{\infty} \frac{x + 1}{x^{2} - x + 1} d x$ $= - \frac{1}{4} \int_{0}^{\infty} \frac{2 x + 1 - 3}{x^{2} + x + 1} d x + \frac{1}{4} \int_{0}^{\infty} \frac{2 x - 1 + 3}{x^{2} - x + 1} d x$ $= \frac{1}{4} {[l n ∣ \frac{x^{2} - x + 1}{x^{2} + x + 1} ∣]}_{0}^{+ \infty} + \frac{3}{4} \int_{0}^{\infty} \frac{d x}{x^{2} - x + 1} + \frac{3}{4} \int_{0}^{\infty} \frac{d x}{x^{2} + x + 1}$ $= 0 + \frac{3}{4} \int_{0}^{\infty} \frac{d x}{x^{2} - x + 1} + \frac{3}{4} \int_{0}^{\infty} \frac{d x}{x^{2} + x + 1}$ $\int_{0}^{\infty} \frac{d x}{x^{2} - x + 1} = \int_{0}^{\infty} \frac{d x}{{(x - \frac{1}{2})}^{2} + \frac{3}{4}} =_{x - \frac{1}{2} = \frac{\sqrt{3}}{2} u} \frac{4}{3} \int_{- \frac{1}{\sqrt{3}}}^{+ \infty} \frac{1}{u^{2} + 1} \frac{\sqrt{3}}{2} d u$ $= \frac{2}{\sqrt{3}} {[a r c t a n u]}_{- \frac{1}{\sqrt{3}}}^{+ \infty} = \frac{2}{\sqrt{3}} {\frac{π}{2} + a r c t a n (\frac{1}{\sqrt{3}})} = \frac{2}{\sqrt{3}} {\frac{π}{2} + \frac{π}{6}}$ $= \frac{2}{\sqrt{3}} {\frac{2 π}{3}} = \frac{4 π}{3 \sqrt{3}}$ $\int_{0}^{\infty} \frac{d x}{x^{2} + x + 1} = \int_{0}^{\infty} \frac{d x}{{(x + \frac{1}{2})}^{2} + \frac{3}{4}} =_{x + \frac{1}{2} = \frac{\sqrt{3}}{2} u} \frac{4}{3} \int_{\frac{1}{\sqrt{3}}}^{\infty} \frac{1}{u^{2} + 1} \frac{\sqrt{3}}{2} d u$ $= \frac{2 \sqrt{3}}{3} {[a r c t a n (u)]}_{\frac{1}{\sqrt{3}}}^{+ \infty} = \frac{2}{\sqrt{3}} {\frac{π}{2} - \frac{π}{6}} = \frac{2}{\sqrt{3}} {\frac{π}{3}} = \frac{2 π}{3 \sqrt{3}} \Rightarrow$ $\int_{0}^{\infty} F (x) d x = \frac{3}{4} \times \frac{4 π}{3 \sqrt{3}} + \frac{3}{4} \times \frac{2 π}{3 \sqrt{3}} = \frac{π}{\sqrt{3}} + \frac{π}{2 \sqrt{3}} = \frac{3}{2} \frac{π}{\sqrt{3}}$ $w e h a v e I = 2 \int_{0}^{\infty} F (x) d x = \frac{3 π}{\sqrt{3}} = π \sqrt{3}$
Commented by MJS last updated on 26/Aug/19

$\int \frac{d x}{x^{4} + x^{2} + 1} =$ $= \int (- \frac{2 x - 1}{4 (x^{2} - x + 1)} + \frac{1}{4 (x^{2} - x + 1)} + \frac{2 x + 1}{4 (x^{2} + x + 1)} + \frac{1}{4 (x^{2} + x + 1)}) d x =$ $= - \frac{1}{4} \ln (x^{2} - x + 1) + \frac{\sqrt{3}}{6} \arctan \frac{\sqrt{3} (2 x - 1)}{3} + \frac{1}{4} \ln (x^{2} + x + 1) + \frac{\sqrt{3}}{6} \arctan \frac{\sqrt{3} (2 x + 1)}{3} =$ $= \frac{1}{4} \ln \frac{x^{2} + x + 1}{x^{2} - x + 1} + \frac{\sqrt{3}}{6} (\arctan \frac{\sqrt{3} (2 x - 1)}{3} + \arctan \frac{\sqrt{3} (2 x + 1)}{3}) + C$ $\underset{- \infty}{\int^{+ \infty}} \frac{d x}{x^{4} + x^{2} + 1} = \frac{π \sqrt{3}}{3}$
	Answered by Kunal12588 last updated on 25/Aug/19

	$\frac{1}{2} \int \frac{\frac{2}{x^{2}}}{x^{2} + 1 + \frac{1}{x^{2}}} d x = \frac{1}{2} \int \frac{1 + \frac{1}{x^{2}}}{x^{2} + \frac{1}{x^{2}} + 1} d x - \frac{1}{2} \int \frac{1 - \frac{1}{x^{2}}}{x^{2} + \frac{1}{x^{2}} + 1} d x$ $(x + \frac{1}{x}) = t \Rightarrow (1 - \frac{1}{x^{2}}) d x = d t$ $(x - \frac{1}{x}) = u \Rightarrow (1 + \frac{1}{x^{2}}) d x = d u$ $x^{2} + \frac{1}{x^{2}} + 1 = t^{2} - 1 a n d x^{2} + \frac{1}{x^{2}} + 1 = u^{2} + 3$ $I = \frac{1}{2} \int \frac{d u}{u^{2} + 3} - \frac{1}{2} \int \frac{d t}{t^{2} - 1}$ $= \frac{1}{2} \times \frac{1}{\sqrt{3}} \times {t a n}^{- 1} (\frac{u}{\sqrt{3}}) - \frac{1}{2} \times \frac{1}{2} l n ∣ \frac{t - 1}{t + 1} ∣ + C$ $= \frac{1}{2 \sqrt{3}} {t a n}^{- 1} (\frac{x^{2} - 1}{x \sqrt{3}}) - \frac{1}{4} l n ∣ \frac{x^{2} - x + 1}{x^{2} + x + 1} ∣ + C$ $I_{1} = \int_{- \infty}^{+ \infty} \frac{d x}{x^{4} + x^{2} + 1} = {[I]}_{- \infty}^{+ \infty}$ $\underset{x \to + \infty}{l i m} I = \frac{1}{2 \sqrt{3}} \underset{x \to + \infty}{l i m a r c t a n} (\frac{x}{\sqrt{3}} - \frac{1}{x \sqrt{3}}) - \frac{1}{4} \underset{x \to + \infty}{l i m} l n ∣ \frac{1 - \frac{1}{x} + \frac{1}{x^{2}}}{1 + \frac{1}{x} + \frac{1}{x^{2}}} ∣$ $= \frac{1}{2 \sqrt{3}} \underset{x \to + \infty}{l i m a r c t a n} (\frac{x}{\sqrt{3}} - \frac{1}{x \sqrt{3}}) - \frac{1}{4} \underset{x \to + \infty}{l i m} l n ∣ 1 ∣$ $= \frac{1}{2 \sqrt{3}} \times \frac{π}{2} - 0 = \frac{π}{4 \sqrt{3}}$ $\underset{x \to - \infty}{l i m I} = \frac{1}{2 \sqrt{3}} \underset{x \to - \infty}{l i m} a r c t a n (\frac{x}{\sqrt{3}} - \frac{1}{x \sqrt{3}}) - 0$ $= \frac{1}{2 \sqrt{3}} \times \frac{- π}{2} = - \frac{π}{4 \sqrt{3}}$ $I_{1} = \frac{π}{4 \sqrt{3}} + \frac{π}{4 \sqrt{3}} = \frac{π}{2 \sqrt{3}}$
	Commented by mathmax by abdo last updated on 25/Aug/19

	$t h a n k s a l o t s f o r t h i s h a r d w o r k .$
	Commented by Kunal12588 last updated on 26/Aug/19

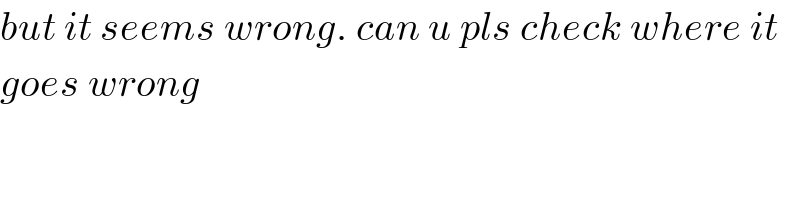
	$b u t i t s e e m s w r o n g . c a n u p l s c h e c k w h e r e i t$ $g o e s w r o n g$
	Commented by mathmax by abdo last updated on 26/Aug/19

	$g i v e o p p o r t u n i t y t o t h e m e t h o d . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum