calculate f(a)=∫_0 ^1 ln(1−ax^3 )dx with 0<a<1


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 78266 by msup trace by abdo last updated on 15/Jan/20

$c a l c u l a t e f (a) = \int_{0}^{1} l n (1 - {a x}^{3}) d x$ $w i t h 0 < a < 1$
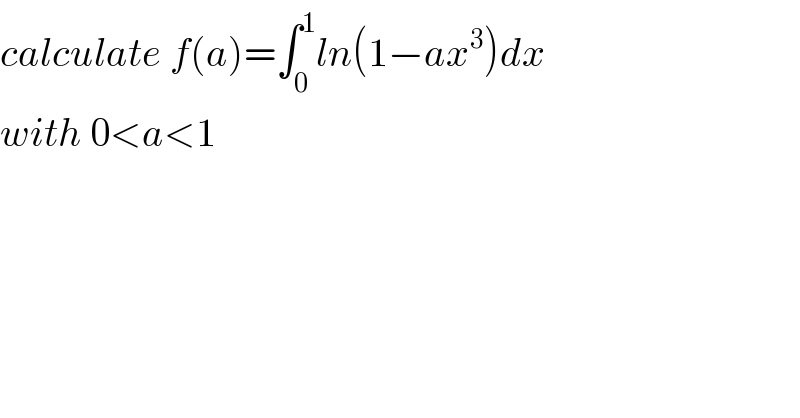
Commented by mathmax by abdo last updated on 18/Jan/20

$f (a) = \int_{0}^{1} l n (1 - {(^{3} \sqrt{a} x)}^{3}) d x =_{(^{3} \sqrt{a} x) = t} \int_{0}^{(^{3} \sqrt{a})} l n (1 - t^{3}) \frac{d t}{(^{3} \sqrt{a})}$ ${= \frac{1}{(^{3} \sqrt{a})} \int_{0}^{(^{3} \sqrt{a})} l n (1 - t^{3}) d t w e h a v e l n (1 - u))}^{(1)} = - \frac{1}{1 - u}$ $= - \sum_{n = 0}^{\infty} u^{n} \Rightarrow l n (1 - u) = - \sum_{n = 0}^{\infty} \frac{u^{n + 1}}{n + 1} = - \sum_{n = 1}^{\infty} \frac{u^{n}}{n}$ $w e h a v e 0 < (^{3} \sqrt{a}) < 1 \Rightarrow l n (1 - t^{3}) = - \sum_{n = 1}^{\infty} \frac{t^{3 n}}{n} \Rightarrow$ $\int_{0}^{(^{3} \sqrt{a})} l n (1 - t^{3}) d t = - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{(^{3} \sqrt{a})} t^{3 n} d t$ $= - \sum_{n = 1}^{\infty} \frac{1}{n (3 n + 1)} {[t^{3 n + 1}]}_{0}^{(^{3} \sqrt{a})} = - \sum_{n = 1}^{\infty} \frac{(^{3} \sqrt{a}) a^{n}}{n (3 n + 1)} \Rightarrow$ $f (a) = - \sum_{n = 1}^{\infty} \frac{a^{n}}{n (3 n + 1)} \Rightarrow - \frac{1}{3} f (a) = \sum_{n = 1}^{\infty} \frac{a^{n}}{3 n (3 n + 1)}$ $= \sum_{n = 1}^{\infty} (\frac{1}{3 n} - \frac{1}{3 n + 1}) a^{n} = \frac{1}{3} \sum_{n = 1}^{\infty} \frac{a^{n}}{n} - \sum_{n = 1}^{\infty} \frac{a^{n}}{3 n + 1}$ $= - \frac{1}{3} l n (1 - a) - \sum_{n = 1}^{\infty} \frac{a^{n}}{3 n + 1}$ $\sum_{n = 1}^{\infty} \frac{a^{n}}{3 n + 1} = \sum_{n = 1}^{\infty} (\frac{{(^{3} \sqrt{a})}^{3 n + 1}}{3 n + 1}) \times \frac{1}{(^{3} \sqrt{a})} = \frac{1}{(^{3} \sqrt{a})} W (^{3} \sqrt{a}) w i t h$ $w (x) = \sum_{n = 1}^{\infty} \frac{x^{3 n + 1}}{3 n + 1} \Rightarrow w^{^{'}} (x) = \sum_{n = 1}^{\infty} x^{3 n} = \frac{1}{1 - x^{3}} - 1 \Rightarrow$ $w (x) = \int_{0}^{x} (\frac{1}{1 - t^{3}} - 1) d t + c = - x + \int_{0}^{x} \frac{d t}{(1 - t^{3})} = - x - \int_{0}^{x} \frac{d t}{t^{3} - 1}$ $l e t d e c o m p o s e F (t) = \frac{1}{t^{3} - 1} = \frac{1}{(t - 1) (t^{2} + t + 1)}$ $F (t) = \frac{a}{t - 1} + \frac{b t + c}{t^{2} + t + 1}$
Commented by mathmax by abdo last updated on 18/Jan/20
$a =(t−1)F(t)∣_(t=1) =(1/3) lim_(t→+∞) tF(t) =0 =a+b ⇒b =−(1/3) F(0)=−a +c =−1 ⇒c =a−1 =(1/3)−1 =−(2/3) ⇒ F(t)=(1/(3(t−1))) −(1/3)((t+2)/(t^2 +t +1)) ⇒ ∫ F(t)dt =(1/3)ln∣t−1∣−(1/6)∫((2t+1+3)/(t^2 +t+1))dt =(1/3)ln∣t−1∣−(1/6)ln(t^2 +t +1)−(1/2) ∫ (dt/(t^2 +t +1)) ∫ (dt/(t^2 +t +1)) =∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (4/3) ∫ (1/(u^2 +1))×((√3)/2)du =(2/(√3)) arctan(((2t+1)/(√3))) ⇒∫_0 ^x F(t)dt =[(1/3)ln∣t−1∣−(1/6)ln(t^2 +t +1)]_0 ^x −(1/(√3))[ arctan(((2t+1)/(√3)))]_0 ^x =(1/3)ln∣x−1∣−(1/6)ln(x^2 +x+1) −(1/(√3)){ arctan(((2x+1)/(√3)))−arctan((1/(√3))) ⇒ w(x)=x−(1/3)ln∣x−1∣+(1/6)ln(x^2 +x+1)+(1/(√3)){ arctan(((2x+1)/(√3)))−(π/6)} ⇒f(a)=−(1/3)ln(1−a)−(1/((^3 (√a))))w(^3 (√a)) f(a) =−(1/3)ln(1−a)−(1/((^3 (√a)))){^3 (√a)−(1/3)ln∣^3 (√a)−1∣+(1/6)ln((^3 (√a))^2 +^3 (√a)+1) +(1/(√3)) arctan(((2(^3 (√a))+1)/(√3)))−(π/(6(√3)))}$
$a = (t - 1) F (t) ∣_{t = 1} = \frac{1}{3}$ ${l i m}_{t \to + \infty} t F (t) = 0 = a + b \Rightarrow b = - \frac{1}{3}$ $F (0) = - a + c = - 1 \Rightarrow c = a - 1 = \frac{1}{3} - 1 = - \frac{2}{3} \Rightarrow$ $F (t) = \frac{1}{3 (t - 1)} - \frac{1}{3} \frac{t + 2}{t^{2} + t + 1} \Rightarrow \int F (t) d t = \frac{1}{3} l n ∣ t - 1 ∣ - \frac{1}{6} \int \frac{2 t + 1 + 3}{t^{2} + t + 1} d t$ $= \frac{1}{3} l n ∣ t - 1 ∣ - \frac{1}{6} l n (t^{2} + t + 1) - \frac{1}{2} \int \frac{d t}{t^{2} + t + 1}$ $\int \frac{d t}{t^{2} + t + 1} = \int \frac{d t}{{(t + \frac{1}{2})}^{2} + \frac{3}{4}} =_{t + \frac{1}{2} = \frac{\sqrt{3}}{2} u} \frac{4}{3} \int \frac{1}{u^{2} + 1} \times \frac{\sqrt{3}}{2} d u$ $= \frac{2}{\sqrt{3}} a r c t a n (\frac{2 t + 1}{\sqrt{3}}) \Rightarrow \int_{0}^{x} F (t) d t = {[\frac{1}{3} l n ∣ t - 1 ∣ - \frac{1}{6} l n (t^{2} + t + 1)]}_{0}^{x}$ $- \frac{1}{\sqrt{3}} {[a r c t a n (\frac{2 t + 1}{\sqrt{3}})]}_{0}^{x} = \frac{1}{3} l n ∣ x - 1 ∣ - \frac{1}{6} l n (x^{2} + x + 1)$ $- \frac{1}{\sqrt{3}} {a r c t a n (\frac{2 x + 1}{\sqrt{3}}) - a r c t a n (\frac{1}{\sqrt{3}}) \Rightarrow$ $w (x) = x - \frac{1}{3} l n ∣ x - 1 ∣ + \frac{1}{6} l n (x^{2} + x + 1) + \frac{1}{\sqrt{3}} {a r c t a n (\frac{2 x + 1}{\sqrt{3}}) - \frac{π}{6}}$ $\Rightarrow f (a) = - \frac{1}{3} l n (1 - a) - \frac{1}{(^{3} \sqrt{a})} w (^{3} \sqrt{a})$ $f (a) = - \frac{1}{3} l n (1 - a) - \frac{1}{(^{3} \sqrt{a})} {^{3} \sqrt{a} - \frac{1}{3} l n ∣^{3} \sqrt{a} - 1 ∣ + \frac{1}{6} l n ({(^{3} \sqrt{a})}^{2} +^{3} \sqrt{a} + 1)$ $+ \frac{1}{\sqrt{3}} a r c t a n (\frac{2 (^{3} \sqrt{a}) + 1}{\sqrt{3}}) - \frac{π}{6 \sqrt{3}}}$
	Answered by mind is power last updated on 15/Jan/20
	$ln(1−ax^3 )= ln(1−ax^3 )=−Σ_(k≥1) ((a^k x^(3k) )/k) f(a)=−∫_0 ^1 Σ_(k≥1) (a^k /k).x^(3k) dx =−Σ_(k≥1) (a^k /(k(3k+1))) =−(1/3){Σ_(k≥1) (a^k /k)−Σ_(k≥1) (a^(3k) /(3k+1))} =−(1/3)Σ_(k≥1) (a^k /k)+(1/3)Σ_(k≥1) (a^(3k) /(3k+1)) =((ln(1−a))/3)+(1/(3a)).Σ_(k≥1) (a^(3k+1) /(3k+1)) g(a)=Σ_(k≥1) (a^(3k+1) /(3k+1))⇒g′(a)=Σ_(k≥1) a^(3k) =(a^3 /(1−a^3 )) g(a)=∫_0 ^a (x^3 /(1−x^3 ))dx=∫_0 ^a (−1+(1/(1−x^3 )))dx =−a+∫_0 ^a (dx/((1−x)(1+x+x^2 )))=−a+∫_0 ^a (1/3){(1/((1−x)))+((x+2)/(1+x+x^2 ))}dx =−a+(1/3)∫_0 ^a ((1/(1−x))+((x+(1/2))/(1+x+x^2 ))+(3/2).(1/((x+(1/2))^2 +(3/4))))dx =−a+((ln(1−a))/3)+(1/6)ln(1+a+a^2 )+(2/3)∫_0 ^a (dx/((((2x+1)/(√3)))^2 +1)) g(a)=−a+((ln(1−a))/3)+((ln(1+a+a^2 ))/6)+(1/(√3)){arctan(((2a+1)/(√3)))−(π/6)} f(a)=((ln(1−a))/3)+(1/(3a))g(a) =−(1/3)+(1/(3a))(aln(1−a)+ln(1−a))+((ln(1+a+a^2 ))/(18a))+(1/(3a(√3))){arctan(((2a+1)/(√3)))−(π/6)}$
	$\ln (1 - {ax}^{3}) =$ $\ln (1 - {ax}^{3}) = - \sum_{k ⩾ 1} \frac{a^{k} x^{3 k}}{k}$ $f (a) = - \int_{0}^{1} \sum_{k ⩾ 1} \frac{a^{k}}{k} . x^{3 k} dx$ $= - \sum_{k ⩾ 1} \frac{a^{k}}{k (3 k + 1)}$ $= - \frac{1}{3} {\sum_{k ⩾ 1} \frac{a^{k}}{k} - \sum_{k ⩾ 1} \frac{a^{3 k}}{3 k + 1}}$ $= - \frac{1}{3} \sum_{k ⩾ 1} \frac{a^{k}}{k} + \frac{1}{3} \sum_{k ⩾ 1} \frac{a^{3 k}}{3 k + 1}$ $= \frac{\ln (1 - a)}{3} + \frac{1}{3 a} . \sum_{k ⩾ 1} \frac{a^{3 k + 1}}{3 k + 1}$ $g (a) = \sum_{k ⩾ 1} \frac{a^{3 k + 1}}{3 k + 1} \Rightarrow g^{'} (a) = \sum_{k ⩾ 1} a^{3 k} = \frac{a^{3}}{1 - a^{3}}$ $g (a) = \int_{0}^{a} \frac{x^{3}}{1 - x^{3}} dx = \int_{0}^{a} (- 1 + \frac{1}{1 - x^{3}}) dx$ $= - a + \int_{0}^{a} \frac{dx}{(1 - x) (1 + x + x^{2})} = - a + \int_{0}^{a} \frac{1}{3} {\frac{1}{(1 - x)} + \frac{x + 2}{1 + x + x^{2}}} dx$ $= - a + \frac{1}{3} \int_{0}^{a} (\frac{1}{1 - x} + \frac{x + \frac{1}{2}}{1 + x + x^{2}} + \frac{3}{2} . \frac{1}{{(x + \frac{1}{2})}^{2} + \frac{3}{4}}) dx$ $= - a + \frac{\ln (1 - a)}{3} + \frac{1}{6} \ln (1 + a + a^{2}) + \frac{2}{3} \int_{0}^{a} \frac{dx}{{(\frac{2 x + 1}{\sqrt{3}})}^{2} + 1}$ $g (a) = - a + \frac{\ln (1 - a)}{3} + \frac{\ln (1 + a + a^{2})}{6} + \frac{1}{\sqrt{3}} {\arctan (\frac{2 a + 1}{\sqrt{3}}) - \frac{π}{6}}$ $f (a) = \frac{\ln (1 - a)}{3} + \frac{1}{3 a} g (a)$ $= - \frac{1}{3} + \frac{1}{3 a} (aln (1 - a) + \ln (1 - a)) + \frac{\ln (1 + a + a^{2})}{18 a} + \frac{1}{3 a \sqrt{3}} {\arctan (\frac{2 a + 1}{\sqrt{3}}) - \frac{π}{6}}$
	Commented by msup trace by abdo last updated on 15/Jan/20

	$t h a n k y o u s i r .$
	Commented by mind is power last updated on 15/Jan/20

	$y^{'} re welcom$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum