calculate f(a) =∫_0 ^∞ e^(−(x^2 +(a/x^2 ))) dx with a>0


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 79107 by mathmax by abdo last updated on 22/Jan/20

$c a l c u l a t e f (a) = \int_{0}^{\infty} e^{- (x^{2} + \frac{a}{x^{2}})} d x w i t h a > 0$
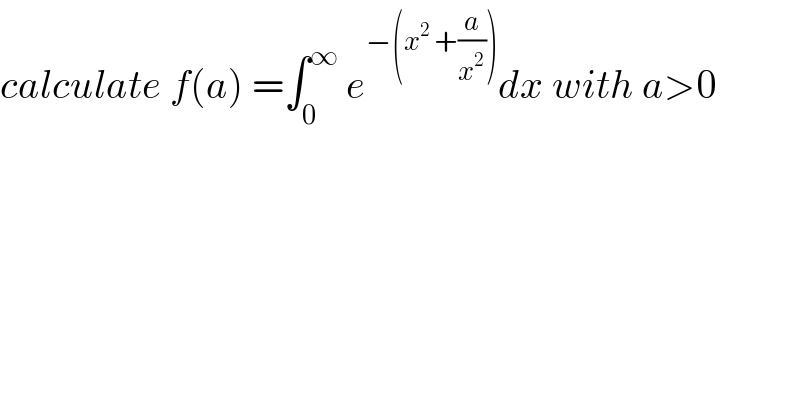
Commented by mathmax by abdo last updated on 23/Jan/20
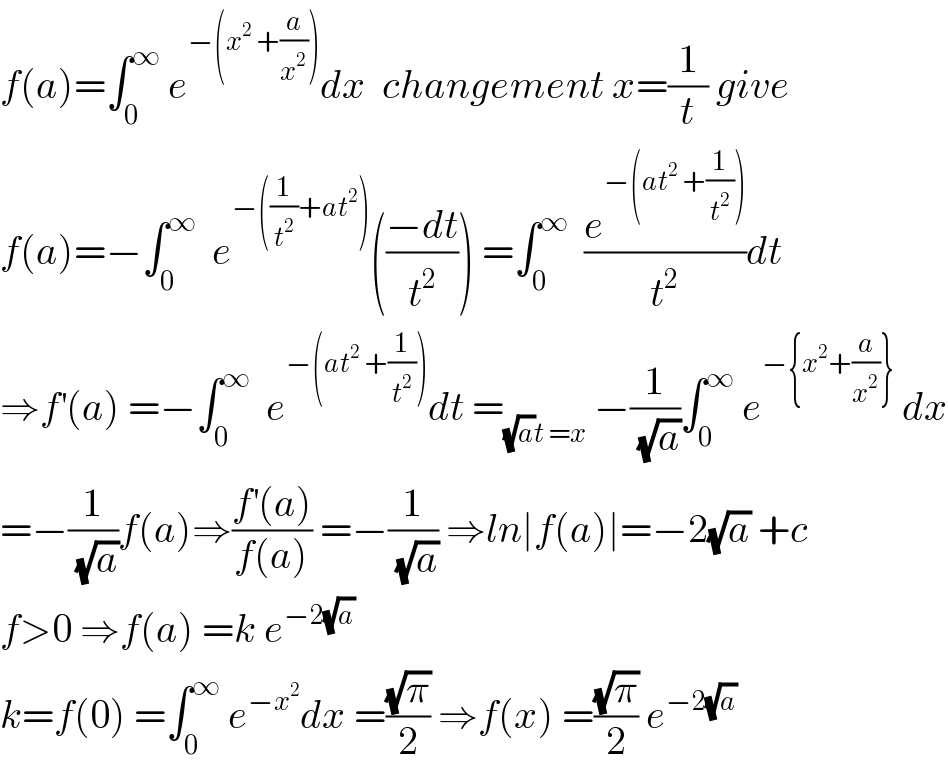
$f(a)=∫_0 ^∞ e^(−(x^2 +(a/x^2 ))) dx changement x=(1/t) give f(a)=−∫_0 ^∞ e^(−((1/t^2 )+at^2 )) (((−dt)/t^2 )) =∫_0 ^∞ (e^(−(at^2 +(1/t^2 ))) /t^2 )dt ⇒f^′ (a) =−∫_0 ^∞ e^(−(at^2 +(1/t^2 ))) dt =_((√a)t =x) −(1/(√a))∫_0 ^∞ e^(−{x^2 +(a/x^2 )}) dx =−(1/(√a))f(a)⇒((f^′ (a))/(f(a))) =−(1/(√a)) ⇒ln∣f(a)∣=−2(√a) +c f>0 ⇒f(a) =k e^(−2(√a)) k=f(0) =∫_0 ^∞ e^(−x^2 ) dx =((√π)/2) ⇒f(x) =((√π)/2) e^(−2(√a))$
$f (a) = \int_{0}^{\infty} e^{- (x^{2} + \frac{a}{x^{2}})} d x c h a n g e m e n t x = \frac{1}{t} g i v e$ $f (a) = - \int_{0}^{\infty} e^{- (\frac{1}{t^{2}} + {a t}^{2})} (\frac{- d t}{t^{2}}) = \int_{0}^{\infty} \frac{e^{- ({a t}^{2} + \frac{1}{t^{2}})}}{t^{2}} d t$ $\Rightarrow f^{^{'}} (a) = - \int_{0}^{\infty} e^{- ({a t}^{2} + \frac{1}{t^{2}})} d t =_{\sqrt{a} t = x} - \frac{1}{\sqrt{a}} \int_{0}^{\infty} e^{- {x^{2} + \frac{a}{x^{2}}}} d x$ $= - \frac{1}{\sqrt{a}} f (a) \Rightarrow \frac{f^{^{'}} (a)}{f (a)} = - \frac{1}{\sqrt{a}} \Rightarrow l n ∣ f (a) ∣= - 2 \sqrt{a} + c$ $f > 0 \Rightarrow f (a) = k e^{- 2 \sqrt{a}}$ $k = f (0) = \int_{0}^{\infty} e^{- x^{2}} d x = \frac{\sqrt{π}}{2} \Rightarrow f (x) = \frac{\sqrt{π}}{2} e^{- 2 \sqrt{a}}$
	Answered by ~blr237~ last updated on 22/Jan/20

	$l e t s t a t e u = \frac{1}{x} t h e n d x = - \frac{d u}{u^{2}}$ $f (a) = \int_{0}^{\infty} e^{- (\frac{1}{u^{2}} + {a u}^{2})} \frac{d u}{u^{2}}$ $f \in C^{1} c a u s e f o r a l l a > 0 ∣ e^{- (x^{2} + \frac{a}{x^{2}})} ∣⩽ e^{- x^{2}} a n d \int_{0}^{\infty} e^{- x^{2}} d x = \frac{\sqrt{π}}{2} s o c o n v e r g e s$ $N o w w e c a n w r i t e$ $\frac{d f}{d a} = - \int_{0}^{\infty} e^{- ({a u}^{2} + \frac{1}{u^{2}})} d u$ $= - \frac{1}{\sqrt{a}} \int_{0}^{\infty} e^{- [{(u \sqrt{a})}^{2} + \frac{a}{{(u \sqrt{a})}^{2}}]} d (u \sqrt{a})$ $= - \frac{1}{\sqrt{a}} \int_{0}^{\infty} e^{- (v^{2} + \frac{a}{v^{2}})} d v w i t h v = u \sqrt{a}$ $S o \frac{d f}{d a} = - \frac{1}{\sqrt{a}} f (a)$ $T h e n l n ∣ f (a) ∣= - 2 \sqrt{a} + c \Rightarrow f (a) = {k e}^{- 2 \sqrt{a}} w i t h k > 0$ $w e k n o w t h a t \lim_{a \to 0} f (a) = k = \frac{\sqrt{π}}{2}$ $F i n a l y f (a) = \frac{\sqrt{π}}{2} e^{- 2 \sqrt{a}}$
	Commented by msup trace by abdo last updated on 22/Jan/20

	$t h a n k s s i r$
	Answered by mind is power last updated on 22/Jan/20

	$o n p o s e x = a^{\frac{1}{4}} u$ $\Rightarrow f (a) = \int_{0}^{+ \infty} a^{\frac{1}{4}} e^{- \sqrt{a} (x^{2} + \frac{1}{x^{2}})} d x$ $x = \frac{1}{y} \Rightarrow$ $= a^{\frac{1}{4}} \int_{0}^{+ \infty} e^{- \sqrt{a} (y^{2} + \frac{1}{y^{2}})} \frac{d y}{y^{2}}$ $\Rightarrow 2 f (a) a^{- \frac{1}{4}} = \int_{0}^{+ \infty} (1 + \frac{1}{y^{2}}) e^{- \sqrt{a} {(y - \frac{1}{y})}^{2} - 2 \sqrt{a}}$ $\Rightarrow 2 f (a) a^{- \frac{1}{4}} e^{2 \sqrt{a}} = \int_{0}^{+ \infty} (1 + \frac{1}{y^{2}}) e^{- \sqrt{a} {(y - \frac{1}{y})}^{2}} d y$ $= \int_{0}^{1} (1 + \frac{1}{y^{2}}) e^{- \sqrt{a} {(y - \frac{1}{y})}^{2}} + \int_{1}^{+ \infty} (1 + \frac{1}{y^{2}}) e^{- \sqrt{a} {(y - \frac{1}{y})}^{2}} d y$ $u = y - \frac{1}{y}, i n f i r s t t = \frac{1}{y} i n 2 n d \Rightarrow$ $\Rightarrow \int_{0}^{+ \infty} e^{- \sqrt{a} u^{2}} d u + \int_{0}^{1} (1 + \frac{1}{t^{2}}) e^{- \sqrt{a} {(t - \frac{1}{t})}^{2}} d t$ $= 2 \int_{0}^{+ \infty} e^{- \sqrt{a} (u^{2})} d u, w = a^{\frac{1}{4}} u \Rightarrow$ $= 2 \int_{0}^{+ \infty} e^{- w^{2}} \frac{d w}{a^{\frac{1}{4}}} = \frac{\sqrt{π}}{a^{\frac{1}{4}}}$ $\Rightarrow 2 f (a) a^{- \frac{1}{4}} e^{2 \sqrt{a}} = \frac{\sqrt{π}}{a^{\frac{1}{4}}} \Rightarrow f (a) = \frac{\sqrt{π}}{2 e^{2 \sqrt{a}}}$
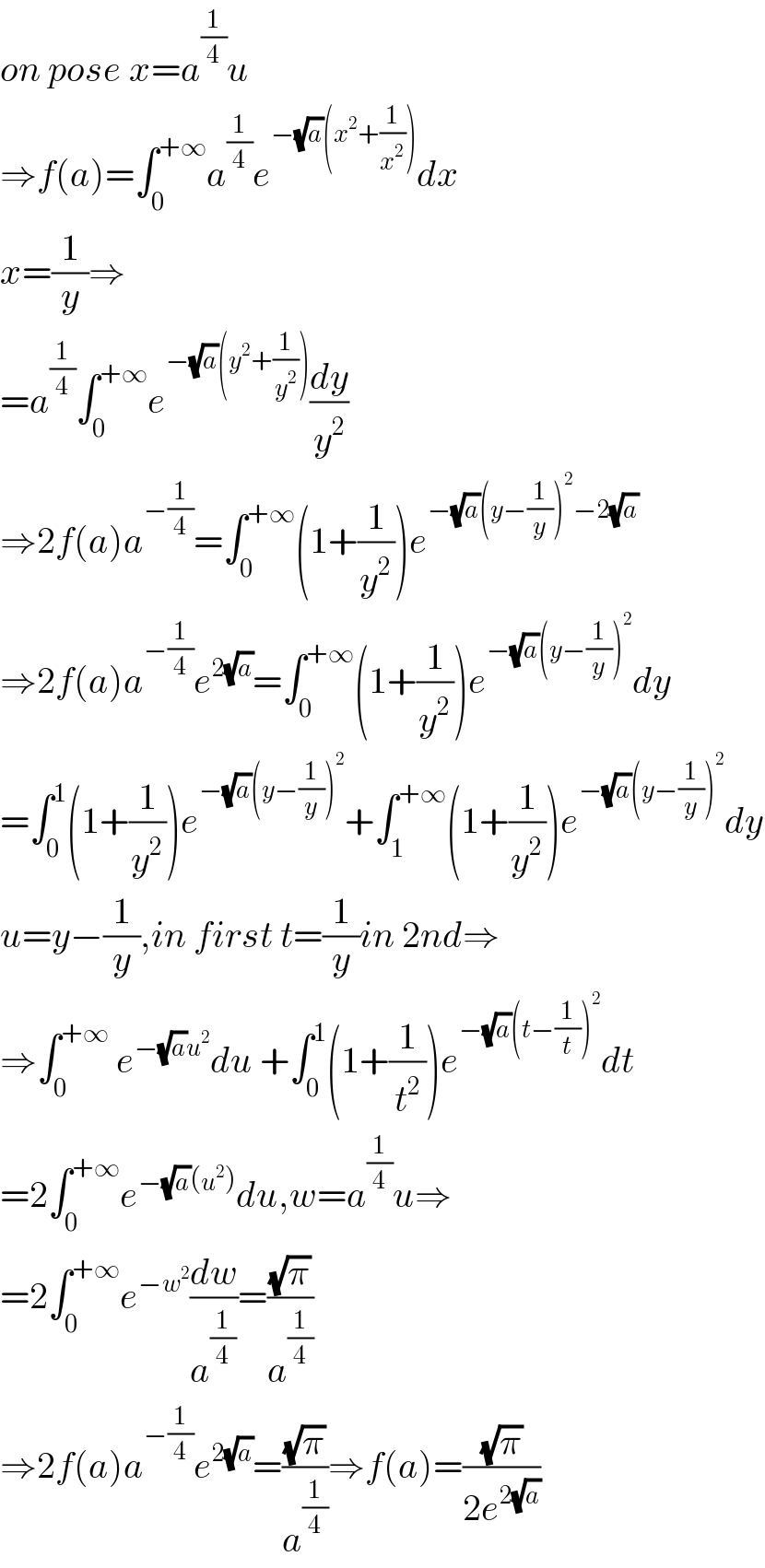
	Commented by msup trace by abdo last updated on 22/Jan/20

	$t h a n k s s i r .$
	Commented by mind is power last updated on 22/Jan/20

	$y^{'} r e w e l c o m$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum