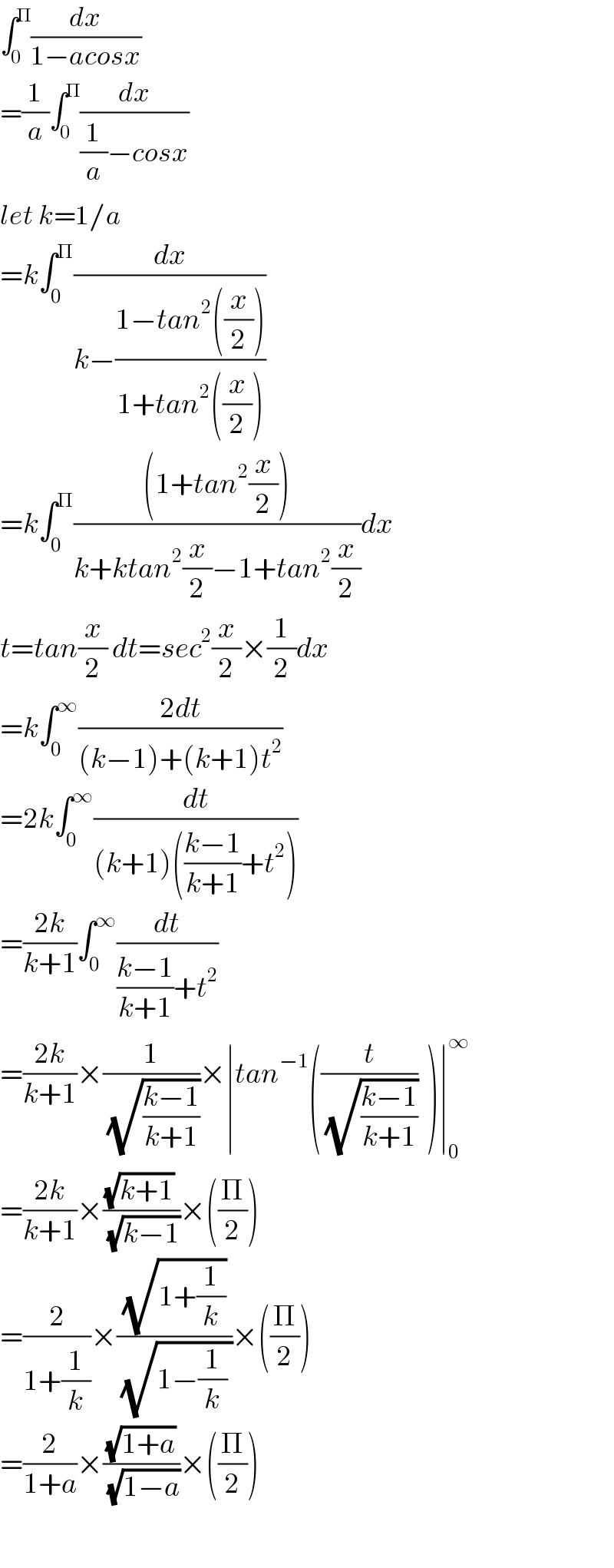calculate f(a)=∫_0 ^π (dx/(1−a cosx)) a from R . 2) application calculate ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 35687 by prof Abdo imad last updated on 22/May/18

$c a l c u l a t e f (a) = \int_{0}^{π} \frac{d x}{1 - a c o s x} a f r o m R .$ $2) a p p l i c a t i o n c a l c u l a t e \int_{0}^{π} \frac{d x}{1 - 2 c o s x}$
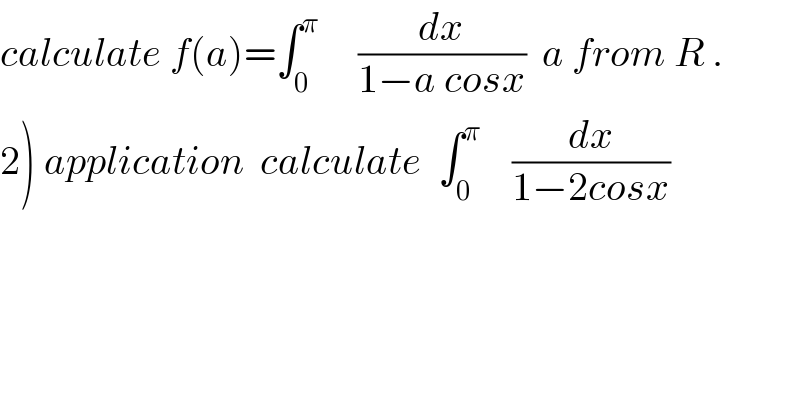
Commented by prof Abdo imad last updated on 22/May/18
$vhangement tan((x/2))=t give f(a) = ∫_0 ^∞ (1/(1−a ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^∞ ((2dt)/(1+t^2 −a(1−t^2 ))) = ∫_0 ^∞ ((2dt)/(1−a +(1+a)t^2 )) = (1/(1−a))∫_0 ^∞ ((2dt)/(1+((1+a)/(1−a))t^2 )) case 1 ((1+a)/(1−a))>0 and a≠1 ⇒ (((1+a)(1−a))/((1−a)^2 ))>0 ⇒ 1−a^2 >0 ⇒ ∣a∣<1 we get f(a) = (2/(1−a))∫_0 ^∞ (dt/(1+((√((1+a)/(1−a)))t)^2 )) =_(u= (√((1+a)/(1−a)))t) (2/(1−a))∫_0 ^∞ (1/(1+u^2 )) ((√(1−a))/(√(1+a))) du =(2/((√(1−a))(√(1+a)))) .(π/2) = (π/(√(1−a^2 ))) case2 ((1+a)/(1−a))<0 ⇒ ((1+a)/(a−1))>0 and f(a) = (1/(1−a))∫_0 ^∞ ((2dt)/(1 −((a+1)/(a−1))t^2 )) =_((√((a+1)/(a−1))) t =u) (2/(1−a)) ∫_0 ^∞ (1/(1 −u^2 )) ((√(a−1))/(√(a+1))) du = −(2/(√(a^2 −1))) ∫_0 ^∞ (du/(1−u^2 )) = (1/(√(a^2 −1))) ∫_0 ^∞ { (1/(u−1)) −(1/(u+1))}du = (1/(√(a^2 −1))) [ln∣((u−1)/(u+1))∣]_0 ^(+∞) =0 .$
$v h a n g e m e n t t a n (\frac{x}{2}) = t g i v e$ $f (a) = \int_{0}^{\infty} \frac{1}{1 - a \frac{1 - t^{2}}{1 + t^{2}}} \frac{2 d t}{1 + t^{2}}$ $= \int_{0}^{\infty} \frac{2 d t}{1 + t^{2} - a (1 - t^{2})} = \int_{0}^{\infty} \frac{2 d t}{1 - a + (1 + a) t^{2}}$ $= \frac{1}{1 - a} \int_{0}^{\infty} \frac{2 d t}{1 + \frac{1 + a}{1 - a} t^{2}}$ $c a s e 1 \frac{1 + a}{1 - a} > 0 a n d a \neq 1 \Rightarrow \frac{(1 + a) (1 - a)}{{(1 - a)}^{2}} > 0 \Rightarrow$ $1 - a^{2} > 0 \Rightarrow ∣ a ∣< 1 w e g e t$ $f (a) = \frac{2}{1 - a} \int_{0}^{\infty} \frac{d t}{1 + {(\sqrt{\frac{1 + a}{1 - a}} t)}^{2}}$ $=_{u = \sqrt{\frac{1 + a}{1 - a}} t} \frac{2}{1 - a} \int_{0}^{\infty} \frac{1}{1 + u^{2}} \frac{\sqrt{1 - a}}{\sqrt{1 + a}} d u$ $= \frac{2}{\sqrt{1 - a} \sqrt{1 + a}} . \frac{π}{2} = \frac{π}{\sqrt{1 - a^{2}}}$ $c a s e 2 \frac{1 + a}{1 - a} < 0 \Rightarrow \frac{1 + a}{a - 1} > 0 a n d$ $f (a) = \frac{1}{1 - a} \int_{0}^{\infty} \frac{2 d t}{1 - \frac{a + 1}{a - 1} t^{2}}$ $=_{\sqrt{\frac{a + 1}{a - 1}} t = u} \frac{2}{1 - a} \int_{0}^{\infty} \frac{1}{1 - u^{2}} \frac{\sqrt{a - 1}}{\sqrt{a + 1}} d u$ $= - \frac{2}{\sqrt{a^{2} - 1}} \int_{0}^{\infty} \frac{d u}{1 - u^{2}}$ $= \frac{1}{\sqrt{a^{2} - 1}} \int_{0}^{\infty} {\frac{1}{u - 1} - \frac{1}{u + 1}} d u$ $= \frac{1}{\sqrt{a^{2} - 1}} {[l n ∣ \frac{u - 1}{u + 1} ∣]}_{0}^{+ \infty} = 0 .$
Commented by prof Abdo imad last updated on 22/May/18

$2) w e h a v e a = 2 a n d ∣ a ∣> 1 \Rightarrow$ $\int_{0}^{π} \frac{d x}{1 - 2 c o s x} = 0$
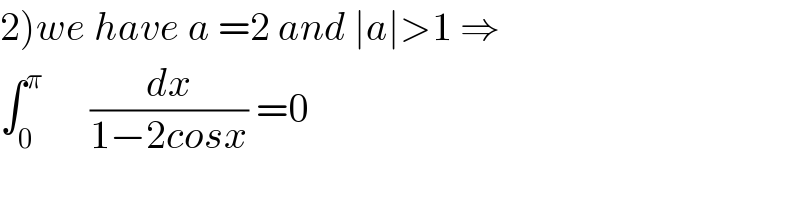
	Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18

	$\int_{0}^{Π} \frac{d x}{1 - a c o s x}$ $= \frac{1}{a} \int_{0}^{Π} \frac{d x}{\frac{1}{a} - c o s x}$ $l e t k = 1 / a$ $= k \int_{0}^{Π} \frac{d x}{k - \frac{1 - {t a n}^{2} (\frac{x}{2})}{1 + {t a n}^{2} (\frac{x}{2})}}$ $= k \int_{0}^{Π} \frac{(1 + {t a n}^{2} \frac{x}{2})}{k + {k t a n}^{2} \frac{x}{2} - 1 + {t a n}^{2} \frac{x}{2}} d x$ $t = t a n \frac{x}{2} d t = {s e c}^{2} \frac{x}{2} \times \frac{1}{2} d x$ $= k \int_{0}^{\infty} \frac{2 d t}{(k - 1) + (k + 1) t^{2}}$ $= 2 k \int_{0}^{\infty} \frac{d t}{(k + 1) (\frac{k - 1}{k + 1} + t^{2})}$ $= \frac{2 k}{k + 1} \int_{0}^{\infty} \frac{d t}{\frac{k - 1}{k + 1} + t^{2}}$ $= \frac{2 k}{k + 1} \times \frac{1}{\sqrt{\frac{k - 1}{k + 1}}} \times ∣ {t a n}^{- 1} (\frac{t}{\sqrt{\frac{k - 1}{k + 1}}}) ∣_{0}^{\infty}$ $= \frac{2 k}{k + 1} \times \frac{\sqrt{k + 1}}{\sqrt{k - 1}} \times (\frac{Π}{2})$ $= \frac{2}{1 + \frac{1}{k}} \times \frac{\sqrt{1 + \frac{1}{k}}}{\sqrt{1 - \frac{1}{k}}} \times (\frac{Π}{2})$ $= \frac{2}{1 + a} \times \frac{\sqrt{1 + a}}{\sqrt{1 - a}} \times (\frac{Π}{2})$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum