calculate f(a) =∫ (dx/((√(1+ax))−(√(1−ax)))) with a>0 . 2) calculate U_n =∫_(−(1/(na))) ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) with n from N and n>1 find lim_(n→+∞) U_n and study the convergence of Σ U


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 54011 by maxmathsup by imad last updated on 27/Jan/19

$c a l c u l a t e f (a) = \int \frac{d x}{\sqrt{1 + a x} - \sqrt{1 - a x}} w i t h a > 0 .$ $2) c a l c u l a t e U_{n} = \int_{- \frac{1}{n a}}^{\frac{1}{n a}} \frac{d x}{\sqrt{1 + a x} - \sqrt{1 - a x}} w i t h n f r o m N a n d n > 1$ $f i n d {l i m}_{n \to + \infty} U_{n} a n d s t u d y t h e c o n v e r g e n c e o f Σ U_{n}$
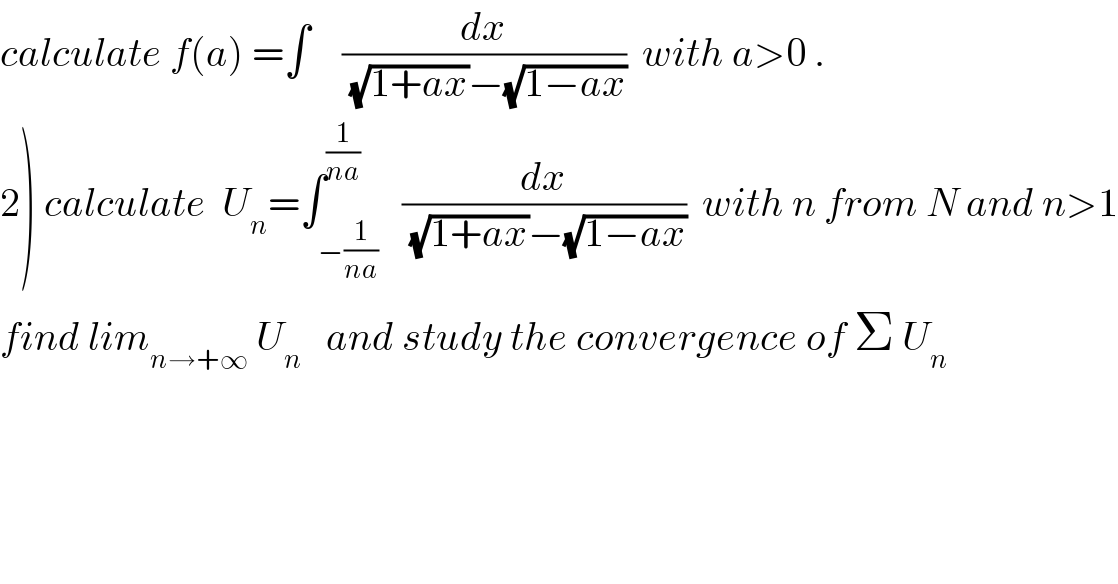
Commented by maxmathsup by imad last updated on 28/Jan/19
$1) we have f(a) =_(ax =t) ∫ (dt/(a((√(1+t))−(√(1−t))))) ⇒ af(a) =∫ (((√(1+t))+(√(1−t)))/(2t)) dt = (1/2) ∫ ((√(1+t))/t)dt +(1/2)∫ ((√(1−t))/t) dt ⇒ 2af(a) = ∫ ((√(1+t))/t) dt +∫ ((√(1−t))/t) dt but ∫ ((√(1+t))/t)dt =_(1+t=u^2 ) ∫ (u/(u^2 −1)) (2u)du =2 ∫ (u^2 /(u^2 −1)) du =2 ∫ ((u^2 −1+1)/(u^2 −1)) =2u +2 ∫ (du/(u^2 −1)) =2u + ∫ ((1/(1−u)) +(1/(1+u)))du =2u +ln∣((1+u)/(1−u))∣ +c_0 =2(√(1+t))+ln∣((1+(√(1+t)))/(1−(√(1−t))))∣ +c_0 =2 (√(1+ax)) +ln∣((1+(√(1+ax)))/(1−(√(1−ax))))∣ +c_0 also we have ∫ ((√(1−t))/t) dt =_(1−t =u^2 ) ∫ (u/(1−u^2 )) (−2u)du = 2 ∫ (u^2 /(u^2 −1)) ⇒ 2af(a) =2 ∫ ((√(1+t))/t) dt ⇒f(a) =(1/a){2(√(1+ax)) +ln∣((1+(√(1+ax)))/(1−(√(1−ax))))∣} . f(a) =(1/a){2(√(1+ax))+ln∣((1+(√(1+ax)))/(1−(√(1−ax))))∣} +C .$
$1) w e h a v e f (a) =_{a x = t} \int \frac{d t}{a (\sqrt{1 + t} - \sqrt{1 - t})} \Rightarrow$ $a f (a) = \int \frac{\sqrt{1 + t} + \sqrt{1 - t}}{2 t} d t = \frac{1}{2} \int \frac{\sqrt{1 + t}}{t} d t + \frac{1}{2} \int \frac{\sqrt{1 - t}}{t} d t \Rightarrow$ $2 a f (a) = \int \frac{\sqrt{1 + t}}{t} d t + \int \frac{\sqrt{1 - t}}{t} d t b u t$ $\int \frac{\sqrt{1 + t}}{t} d t =_{1 + t = u^{2}} \int \frac{u}{u^{2} - 1} (2 u) d u = 2 \int \frac{u^{2}}{u^{2} - 1} d u$ $= 2 \int \frac{u^{2} - 1 + 1}{u^{2} - 1} = 2 u + 2 \int \frac{d u}{u^{2} - 1} = 2 u + \int (\frac{1}{1 - u} + \frac{1}{1 + u}) d u$ $= 2 u + l n ∣ \frac{1 + u}{1 - u} ∣ + c_{0} = 2 \sqrt{1 + t} + l n ∣ \frac{1 + \sqrt{1 + t}}{1 - \sqrt{1 - t}} ∣ + c_{0}$ $= 2 \sqrt{1 + a x} + l n ∣ \frac{1 + \sqrt{1 + a x}}{1 - \sqrt{1 - a x}} ∣ + c_{0} a l s o w e h a v e$ $\int \frac{\sqrt{1 - t}}{t} d t =_{1 - t = u^{2}} \int \frac{u}{1 - u^{2}} (- 2 u) d u = 2 \int \frac{u^{2}}{u^{2} - 1} \Rightarrow$ $2 a f (a) = 2 \int \frac{\sqrt{1 + t}}{t} d t \Rightarrow f (a) = \frac{1}{a} {2 \sqrt{1 + a x} + l n ∣ \frac{1 + \sqrt{1 + a x}}{1 - \sqrt{1 - a x}} ∣} .$ $f (a) = \frac{1}{a} {2 \sqrt{1 + a x} + l n ∣ \frac{1 + \sqrt{1 + a x}}{1 - \sqrt{1 - a x}} ∣} + C .$
Commented by maxmathsup by imad last updated on 28/Jan/19
$2) we have U_n =∫_(−(1/(na))) ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) =2lim_(ξ→0) ∫_ξ ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) but ∫_ξ ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) =[(1/a)(2(√(1+ax))+ln∣((1+(√(1+ax)))/(1−(√(1−ax))))∣)]_(x=ξ) ^(1/(na)) =(1/a){2(√(1+(1/n)))+ln∣((1+(√(1+(1/n))))/(1−(√(1−(1/n)))))∣−2(√(1+aξ))−ln∣((1+(√(1+aξ)))/(1−(√(1−aξ))))∣} but we cant find lim U_n from this quantity be continued...$
$2) w e h a v e U_{n} = \int_{- \frac{1}{n a}}^{\frac{1}{n a}} \frac{d x}{\sqrt{1 + a x} - \sqrt{1 - a x}} = 2 {l i m}_{ξ \to 0} \int_{ξ}^{\frac{1}{n a}} \frac{d x}{\sqrt{1 + a x} - \sqrt{1 - a x}}$ $b u t \int_{ξ}^{\frac{1}{n a}} \frac{d x}{\sqrt{1 + a x} - \sqrt{1 - a x}} = {[\frac{1}{a} (2 \sqrt{1 + a x} + l n ∣ \frac{1 + \sqrt{1 + a x}}{1 - \sqrt{1 - a x}} ∣)]}_{x = ξ}^{\frac{1}{n a}}$ $= \frac{1}{a} {2 \sqrt{1 + \frac{1}{n}} + l n ∣ \frac{1 + \sqrt{1 + \frac{1}{n}}}{1 - \sqrt{1 - \frac{1}{n}}} ∣ - 2 \sqrt{1 + a ξ} - l n ∣ \frac{1 + \sqrt{1 + a ξ}}{1 - \sqrt{1 - a ξ}} ∣}$ $b u t w e c a n t f i n d l i m U_{n} f r o m t h i s q u a n t i t y b e c o n t i n u e d . . .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19

	$\int \frac{\sqrt{1 + a x} + \sqrt{1 - a x}}{2 a x} d x$ $\int \frac{\sqrt{1 + a x}}{2 a x} d x + \int \frac{\sqrt{1 - a x}}{2 a x} d x$ $t_{1}^{2} = 1 + a x 2 t_{1} d t = a d x$ $t_{2}^{2} = 1 - a x 2 t_{2} d t = - a d x$ $\int \frac{t_{1} \times 2 t_{1} d t}{2 a (t_{1}^{2} - 1)} + \int \frac{t_{2} \times - 2 t_{2}}{2 a \times (1 - t_{1}^{2})} {d t}_{2}$ $\frac{1}{a} \int \frac{t_{1}^{2} - 1 + 1}{t_{1}^{2} - 1} {d t}_{1} + \frac{1}{a} \int \frac{1 - t_{2}^{2} - 1}{1 - t_{2}^{2}} {d t}_{2}$ $\frac{1}{a} [\int {d t}_{1} + \int \frac{{d t}_{1}}{t_{2}^{2} - 1} + \int {d t}_{2} - \int \frac{{d t}_{2}}{1 - t_{2}^{2}}]$ $n o w u s e f o r m u l a . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum