
Question and Answers Forum
Question Number 72988 by mathmax by abdo last updated on 05/Nov/19
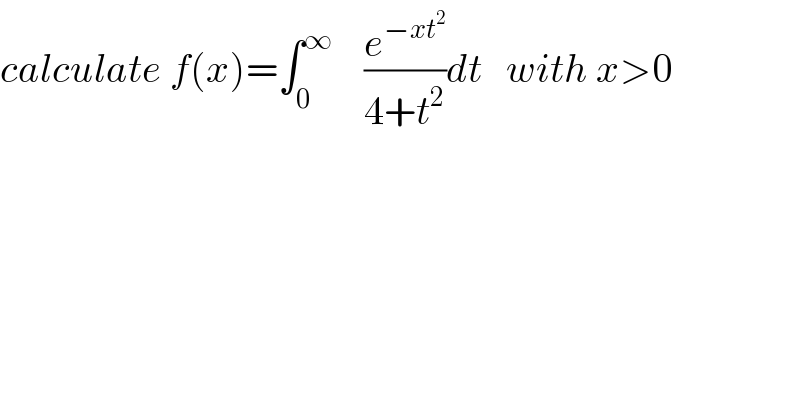
Commented by mathmax by abdo last updated on 05/Nov/19
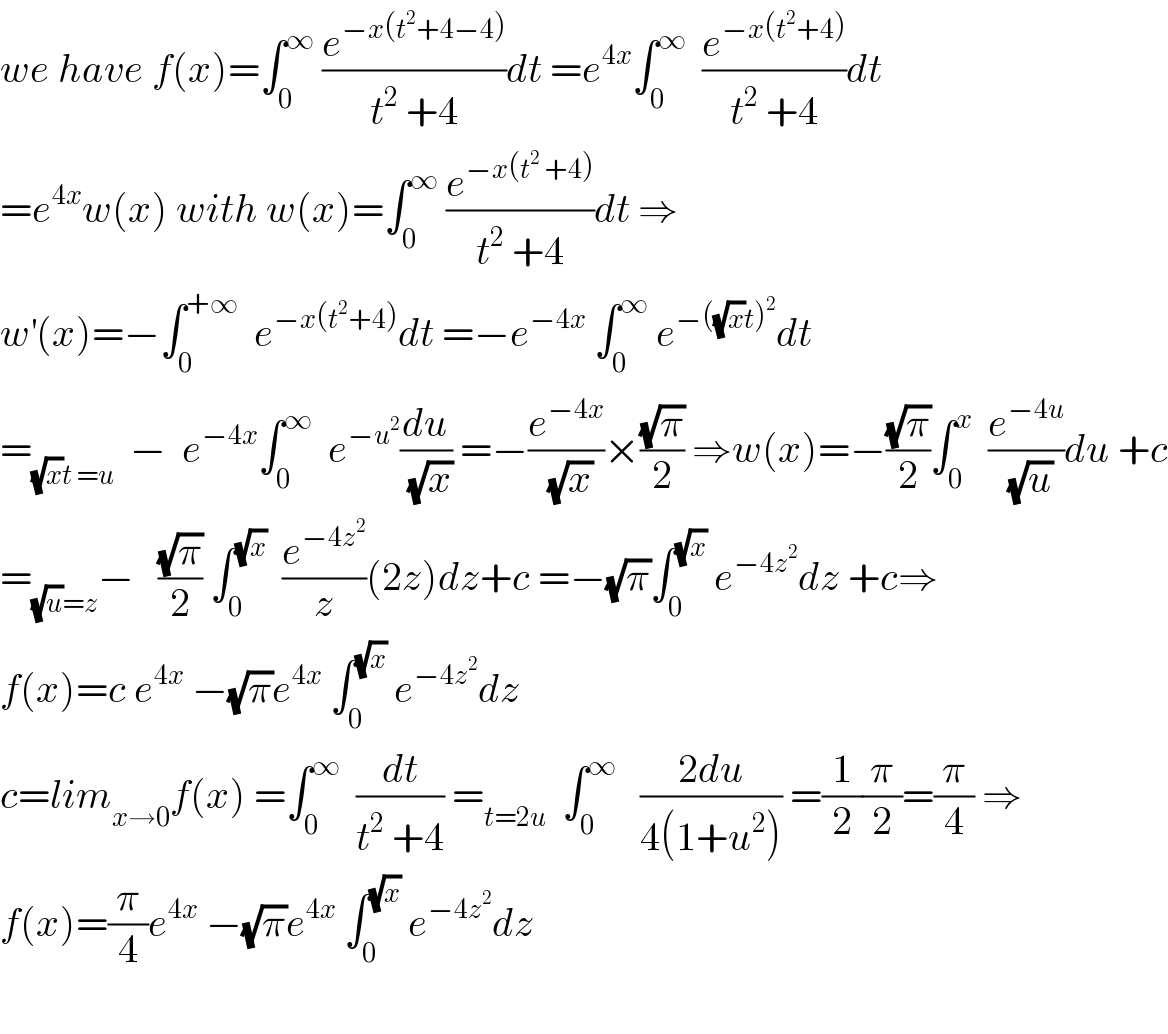
Answered by mind is power last updated on 05/Nov/19
![f′(x)=∫_0 ^(+∞) ((−t^2 e^(−xt^2 ) )/(4+t^2 ))=∫−e^(−xt^2 ) +4∫_0 ^(+∞) (e^(−xt^2 ) /(4+t^2 ))dt =⇒f′(x)=4f(x)−(1/(√x))∫_0 ^(+∞) e^(−(t(√x))^2 ) .(√x)dt ⇒f′(x)=4f(x)−(1/(√x)).∫_0 ^(+∞) e^(−u^2 ) du=4f(x)−(1/(2(√x))).(√(π/2)) f′(x)−4f(x)+(1/(2(√x))).(√(π/2))=0 f(x)=ke^(4x) ⇒k′(x)=−(e^(−4x) /(2(√x)))(√(π/2)) =⇒k(x)=−((√π)/(2(√2)))∫(e^(−4x) /(2(√x)))dx erf(x)=∫_0 ^x e^(−t^2 ) dt (√x)=u⇒k(x)=−((√π)/(2(√2)))∫e^(−4u^2 ) du=−((√π)/(4(√2)))∫e^(−w^2 ) dw=−((√π)/(4(√2)))erf(w) =((√π)/(4(√2)))erf(2u)=−((√π)/(4(√2)))erf(2(√x))+c ⇒f(x)=ce^(−4x) −((√π)/(4(√2)))erf(2(√x))e^(−4x) f(0)=∫_0 ^(+∞) (1/(4+t^2 ))=[(1/2).arctan((t/2))]=(π/4) ⇒c=(π/4) f(x)=(π/4)e^(−4x) −((√π)/(4(√2)))erf(2(√x))e^(−4x)](Q73011.png)
| ||
Question and Answers Forum | ||
Question Number 72988 by mathmax by abdo last updated on 05/Nov/19 | ||
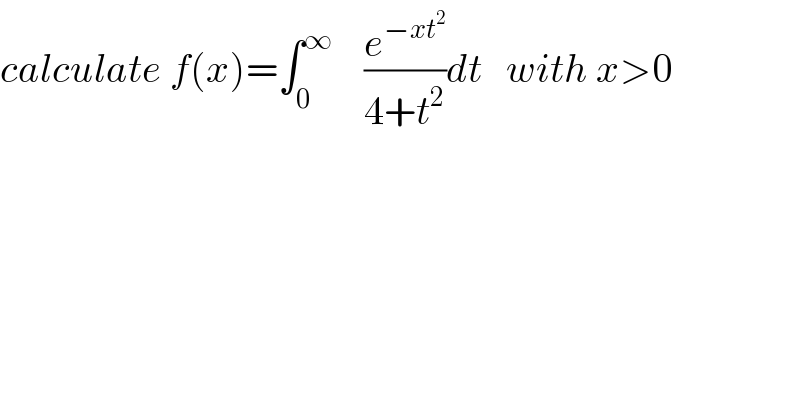 | ||
Commented by mathmax by abdo last updated on 05/Nov/19 | ||
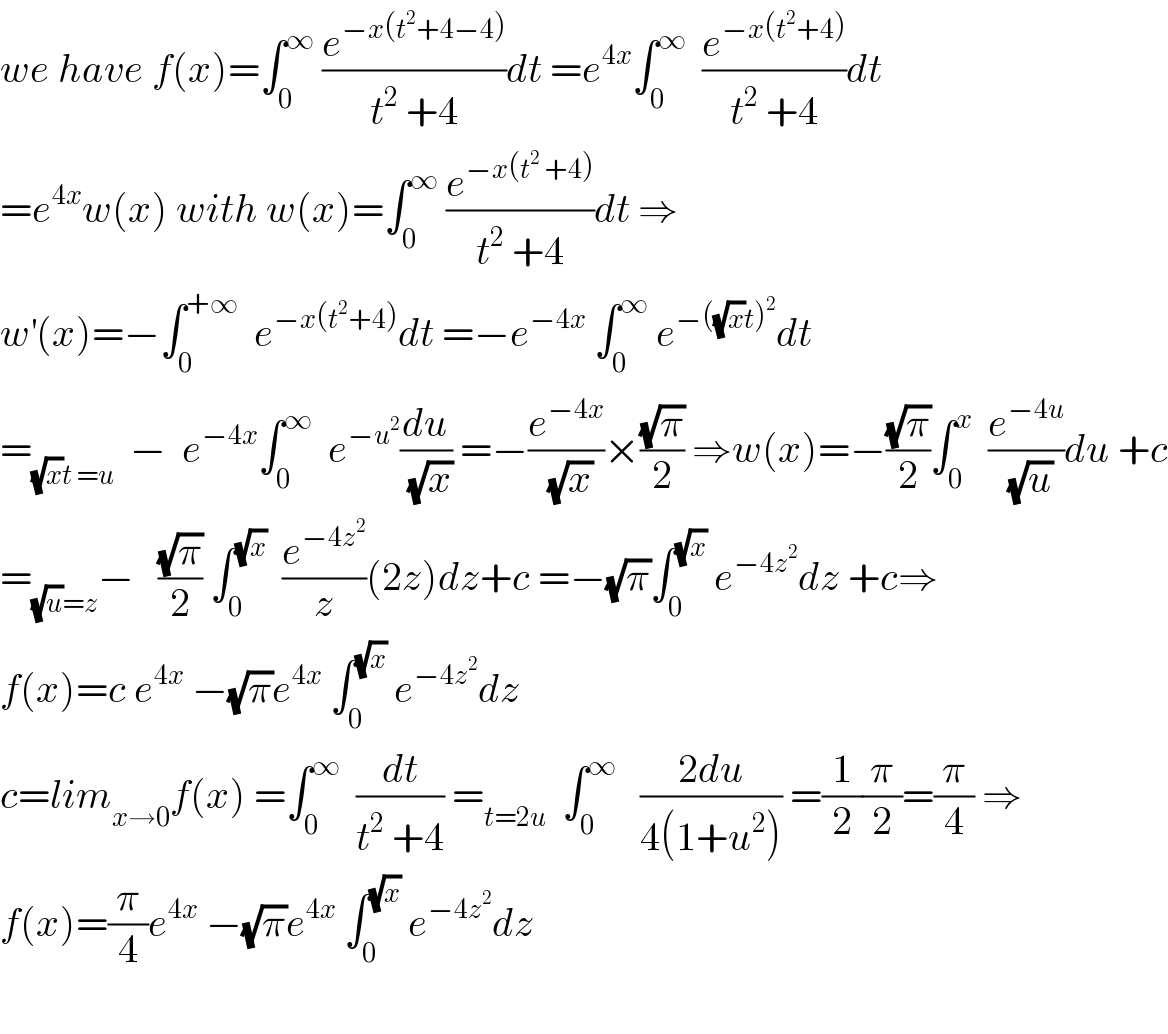 | ||
Answered by mind is power last updated on 05/Nov/19 | ||
![f′(x)=∫_0 ^(+∞) ((−t^2 e^(−xt^2 ) )/(4+t^2 ))=∫−e^(−xt^2 ) +4∫_0 ^(+∞) (e^(−xt^2 ) /(4+t^2 ))dt =⇒f′(x)=4f(x)−(1/(√x))∫_0 ^(+∞) e^(−(t(√x))^2 ) .(√x)dt ⇒f′(x)=4f(x)−(1/(√x)).∫_0 ^(+∞) e^(−u^2 ) du=4f(x)−(1/(2(√x))).(√(π/2)) f′(x)−4f(x)+(1/(2(√x))).(√(π/2))=0 f(x)=ke^(4x) ⇒k′(x)=−(e^(−4x) /(2(√x)))(√(π/2)) =⇒k(x)=−((√π)/(2(√2)))∫(e^(−4x) /(2(√x)))dx erf(x)=∫_0 ^x e^(−t^2 ) dt (√x)=u⇒k(x)=−((√π)/(2(√2)))∫e^(−4u^2 ) du=−((√π)/(4(√2)))∫e^(−w^2 ) dw=−((√π)/(4(√2)))erf(w) =((√π)/(4(√2)))erf(2u)=−((√π)/(4(√2)))erf(2(√x))+c ⇒f(x)=ce^(−4x) −((√π)/(4(√2)))erf(2(√x))e^(−4x) f(0)=∫_0 ^(+∞) (1/(4+t^2 ))=[(1/2).arctan((t/2))]=(π/4) ⇒c=(π/4) f(x)=(π/4)e^(−4x) −((√π)/(4(√2)))erf(2(√x))e^(−4x)](Q73011.png) | ||
| ||