
Question and Answers Forum
Question Number 40142 by maxmathsup by imad last updated on 16/Jul/18
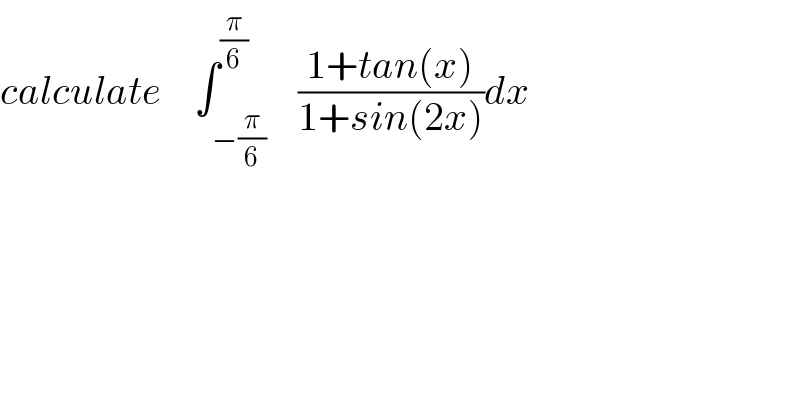
Commented by maxmathsup by imad last updated on 19/Jul/18
![let I = ∫_(−(π/6)) ^(π/6) ((1+tan(x))/(1+sin(2x)))dx changement tanx =t give I = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+((2t)/(1+t^2 )))) (dt/(1+t^2 )) = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+t^2 +2t)) dt = ∫_(−(1/(√3))) ^(1/(√3)) ((t+1)/((t+1)^2 ))dt = ∫_(−(1/(√3))) ^(1/(√3)) (dt/(t+1)) =[ln∣t+1∣]_(−(1/(√3))) ^(1/(√3)) =ln(1+(1/(√3)))−ln(1−(1/(√3)))=ln((√3)+1)−ln((√3)) −ln((√3)−1) +ln((√3)) I=ln((√3) +1) −ln((√3)−1)](Q40342.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jul/18
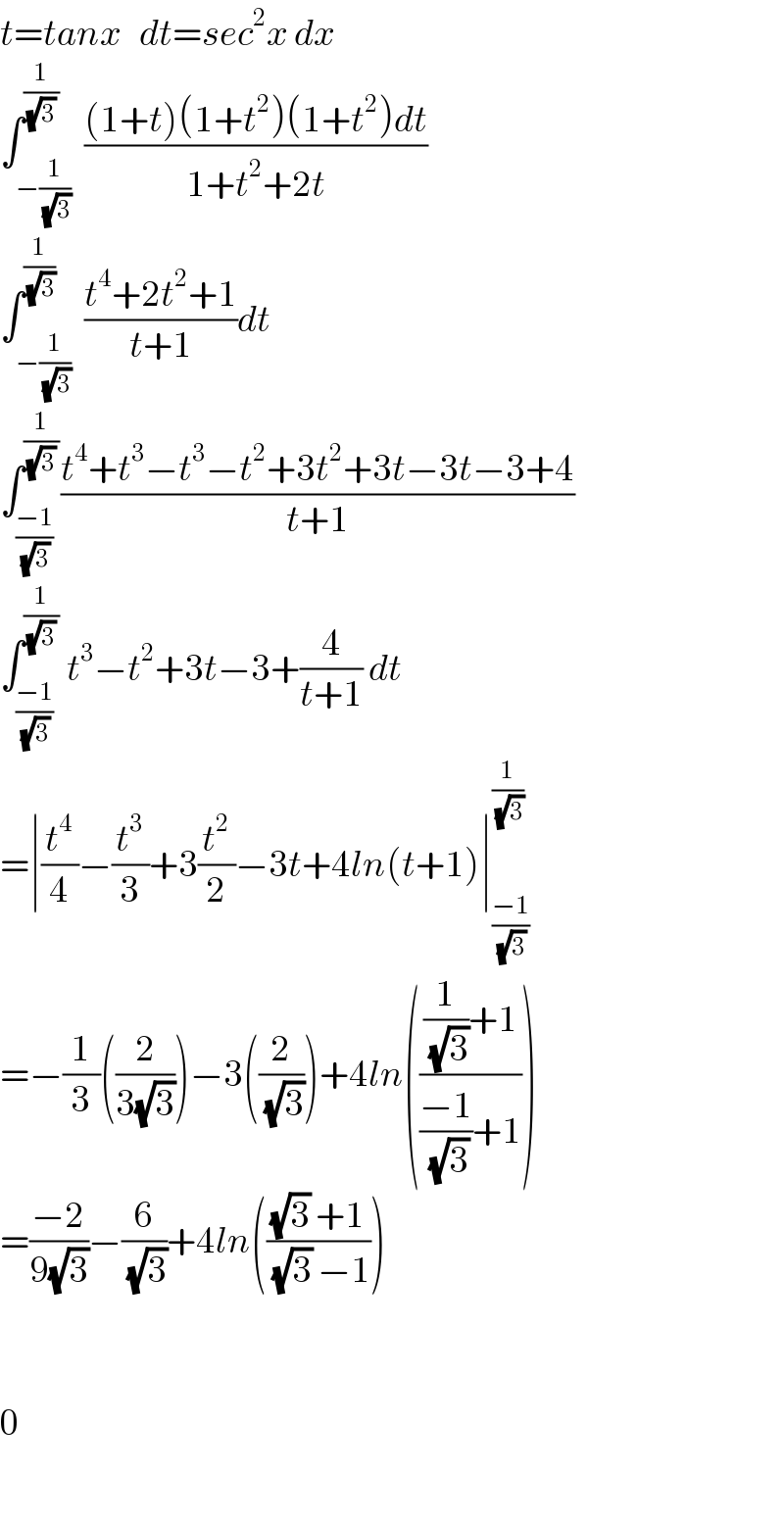
| ||
Question and Answers Forum | ||
Question Number 40142 by maxmathsup by imad last updated on 16/Jul/18 | ||
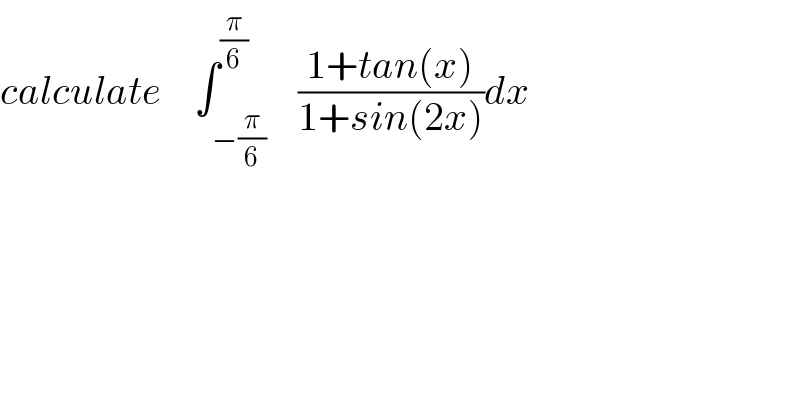 | ||
Commented by maxmathsup by imad last updated on 19/Jul/18 | ||
![let I = ∫_(−(π/6)) ^(π/6) ((1+tan(x))/(1+sin(2x)))dx changement tanx =t give I = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+((2t)/(1+t^2 )))) (dt/(1+t^2 )) = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+t^2 +2t)) dt = ∫_(−(1/(√3))) ^(1/(√3)) ((t+1)/((t+1)^2 ))dt = ∫_(−(1/(√3))) ^(1/(√3)) (dt/(t+1)) =[ln∣t+1∣]_(−(1/(√3))) ^(1/(√3)) =ln(1+(1/(√3)))−ln(1−(1/(√3)))=ln((√3)+1)−ln((√3)) −ln((√3)−1) +ln((√3)) I=ln((√3) +1) −ln((√3)−1)](Q40342.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jul/18 | ||
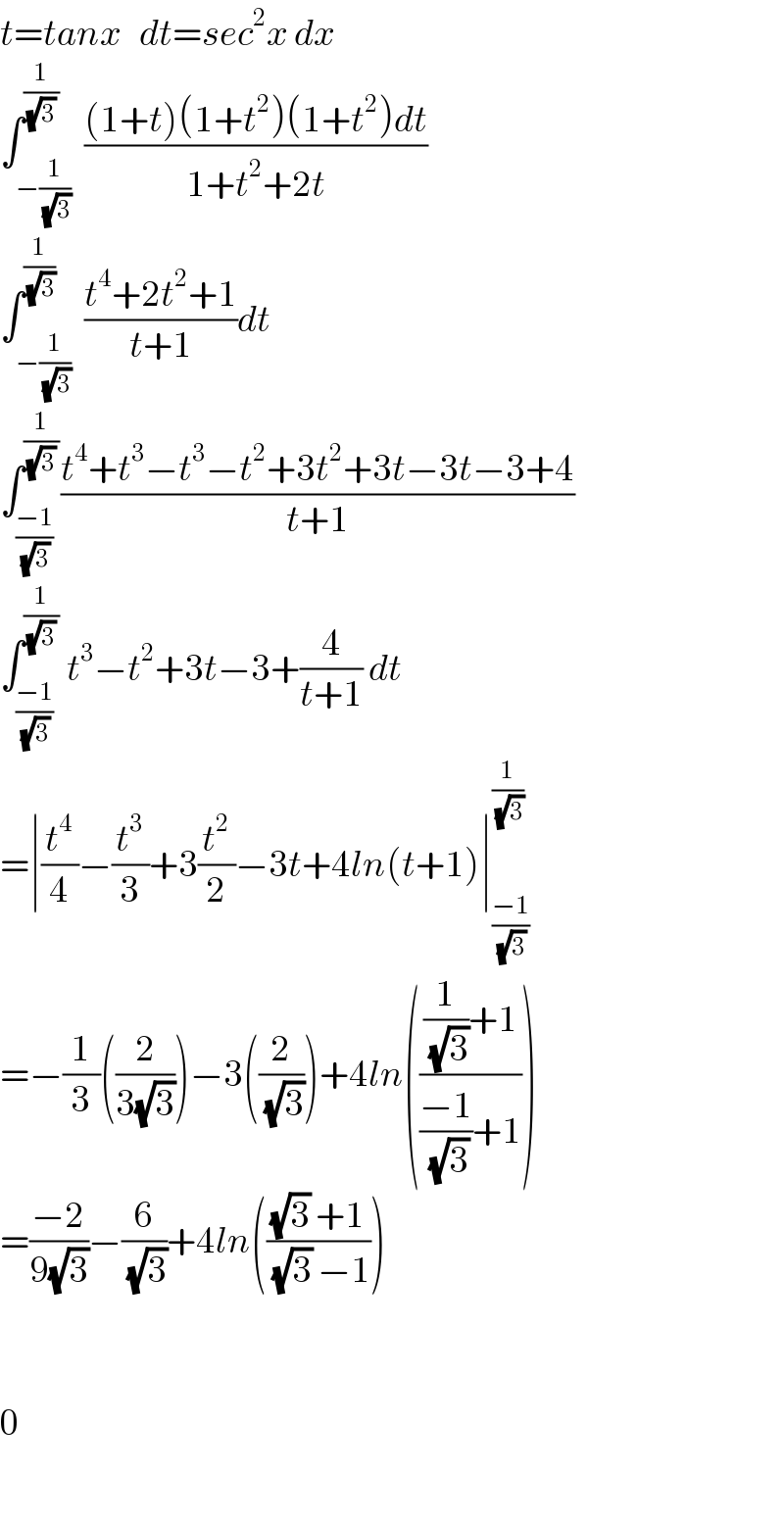 | ||
| ||