
Question and Answers Forum
Question Number 65924 by mathmax by abdo last updated on 05/Aug/19
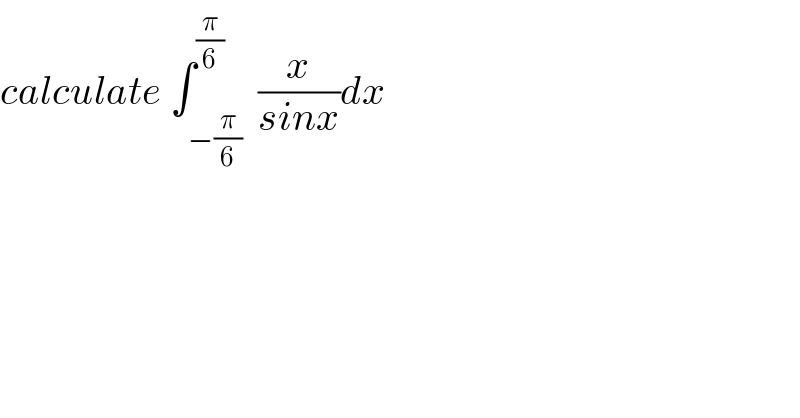
Commented by mathmax by abdo last updated on 07/Aug/19
![let I =∫_(−(π/6)) ^(π/6) (x/(sinx))dx let find approximate value we have I =2∫_0 ^(π/6) (x/(sinx))dx but sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) with radiusR=+∞ ⇒sinx =x−(x^3 /(3!)) +(x^5 /(5!))−....⇒x−(x^3 /(3!))≤sinx ≤x ⇒(1/x)≤(1/(sinx))≤(1/(x−(x^3 /6))) ⇒1≤(x/(sinx))≤(1/(1−(x^2 /6))) for x∈]0,(π/6)] ⇒∫_0 ^(π/6) 1dx ≤∫_0 ^(π/6) (x/(sinx))dx≤∫_0 ^(π/6) ((6dx)/(6−x^2 )) (π/3)≤ 2∫_0 ^(π/6) (x/(sinx))dx ≤12 ∫_0 ^(π/6) (dx/(6−x^2 )) ⇒(π/3)≤I ≤12∫_0 ^(π/6) (dx/(6−x^2 )) ∫_0 ^(π/6) (dx/(6−x^2 )) =−∫_0 ^(π/6) (dx/((x−(√6))(x+(√6)))) =−(1/(2(√6)))∫_0 ^(π/6) {(1/(x−(√6)))−(1/(x+(√6)))}dx =−(1/(2(√6)))[ln∣((x−(√6))/(x+(√6)))∣]_0 ^(π/6) =−(1/(2(√6)))ln∣(((π/6)−(√6))/((π/6)+(√6)))∣ =−(1/(2(√6)))ln∣((π−6(√6))/(π+6(√6)))∣ =(1/(2(√6)))ln(((π+6(√6))/(6(√6)−π))) ⇒(π/3)≤ I ≤(√6)ln(((6(√6)+π)/(6(√6)−π))) let v_0 =(π/6) +((√6)/2)ln(((6(√6)+π)/(6(√6)−π))) v_0 is a better approximation for I .](Q66007.png)
| ||
Question and Answers Forum | ||
Question Number 65924 by mathmax by abdo last updated on 05/Aug/19 | ||
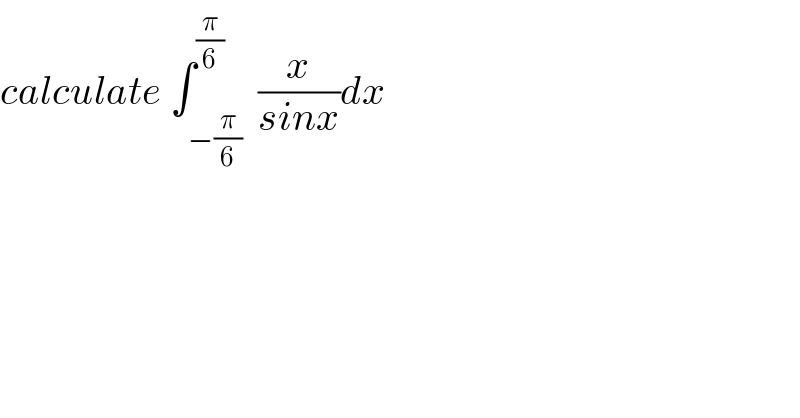 | ||
Commented by mathmax by abdo last updated on 07/Aug/19 | ||
![let I =∫_(−(π/6)) ^(π/6) (x/(sinx))dx let find approximate value we have I =2∫_0 ^(π/6) (x/(sinx))dx but sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) with radiusR=+∞ ⇒sinx =x−(x^3 /(3!)) +(x^5 /(5!))−....⇒x−(x^3 /(3!))≤sinx ≤x ⇒(1/x)≤(1/(sinx))≤(1/(x−(x^3 /6))) ⇒1≤(x/(sinx))≤(1/(1−(x^2 /6))) for x∈]0,(π/6)] ⇒∫_0 ^(π/6) 1dx ≤∫_0 ^(π/6) (x/(sinx))dx≤∫_0 ^(π/6) ((6dx)/(6−x^2 )) (π/3)≤ 2∫_0 ^(π/6) (x/(sinx))dx ≤12 ∫_0 ^(π/6) (dx/(6−x^2 )) ⇒(π/3)≤I ≤12∫_0 ^(π/6) (dx/(6−x^2 )) ∫_0 ^(π/6) (dx/(6−x^2 )) =−∫_0 ^(π/6) (dx/((x−(√6))(x+(√6)))) =−(1/(2(√6)))∫_0 ^(π/6) {(1/(x−(√6)))−(1/(x+(√6)))}dx =−(1/(2(√6)))[ln∣((x−(√6))/(x+(√6)))∣]_0 ^(π/6) =−(1/(2(√6)))ln∣(((π/6)−(√6))/((π/6)+(√6)))∣ =−(1/(2(√6)))ln∣((π−6(√6))/(π+6(√6)))∣ =(1/(2(√6)))ln(((π+6(√6))/(6(√6)−π))) ⇒(π/3)≤ I ≤(√6)ln(((6(√6)+π)/(6(√6)−π))) let v_0 =(π/6) +((√6)/2)ln(((6(√6)+π)/(6(√6)−π))) v_0 is a better approximation for I .](Q66007.png) | ||