
Question and Answers Forum
Question Number 36427 by prof Abdo imad last updated on 02/Jun/18
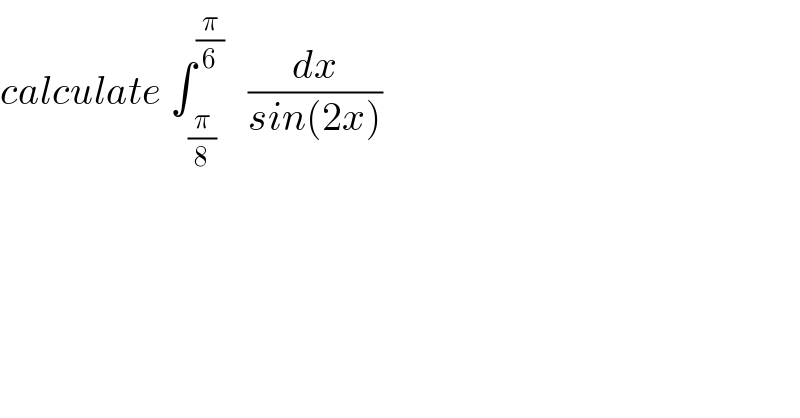
Commented by abdo mathsup 649 cc last updated on 03/Jun/18
![I =_(2x =u) ∫_(π/4) ^(π/3) (1/(sin(u))) (du/2) = (1/2) ∫_(π/4) ^(π/3) (du/(sinu)) and changement tan((u/2))=x give I = (1/2) ∫_((√2) −1) ^(1/(√3)) (1/((2x)/(1+x^2 ))) ((2dx)/(1+x^2 )) = (1/2) ∫_((√2)−1) ^(1/(√3)) (dx/x) =(1/2)[ln ∣x∣]_((√2) −1) ^(1/(√3)) = (1/2){ −ln((√3)) −ln((√2) −1) =−(1/2){ (1/2)ln(3) +ln((√2) −1)} .](Q36522.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18
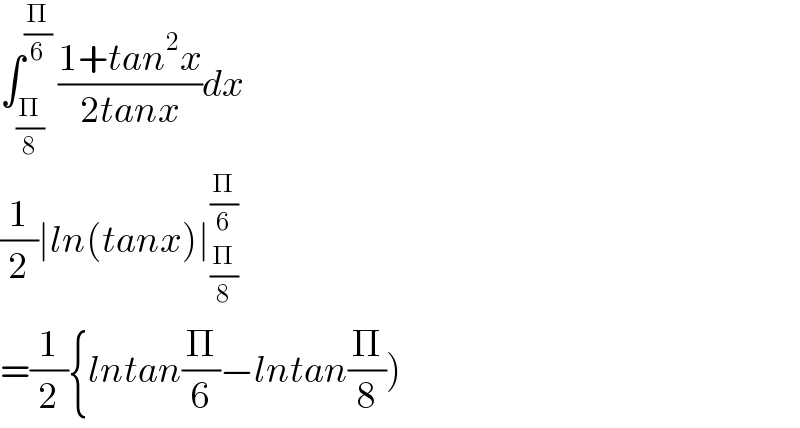
| ||
Question and Answers Forum | ||
Question Number 36427 by prof Abdo imad last updated on 02/Jun/18 | ||
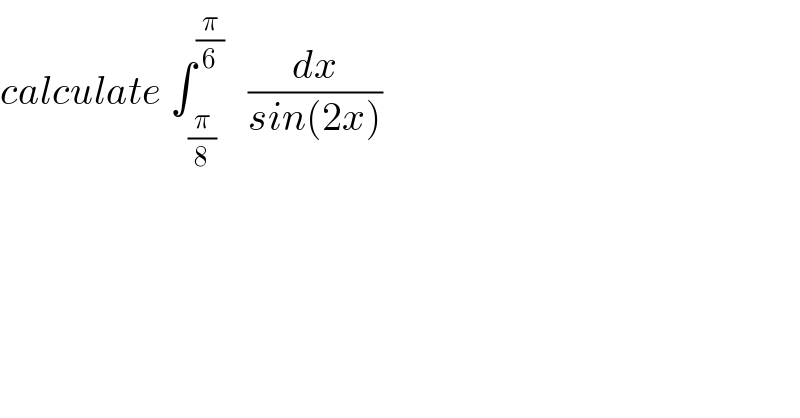 | ||
Commented by abdo mathsup 649 cc last updated on 03/Jun/18 | ||
![I =_(2x =u) ∫_(π/4) ^(π/3) (1/(sin(u))) (du/2) = (1/2) ∫_(π/4) ^(π/3) (du/(sinu)) and changement tan((u/2))=x give I = (1/2) ∫_((√2) −1) ^(1/(√3)) (1/((2x)/(1+x^2 ))) ((2dx)/(1+x^2 )) = (1/2) ∫_((√2)−1) ^(1/(√3)) (dx/x) =(1/2)[ln ∣x∣]_((√2) −1) ^(1/(√3)) = (1/2){ −ln((√3)) −ln((√2) −1) =−(1/2){ (1/2)ln(3) +ln((√2) −1)} .](Q36522.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18 | ||
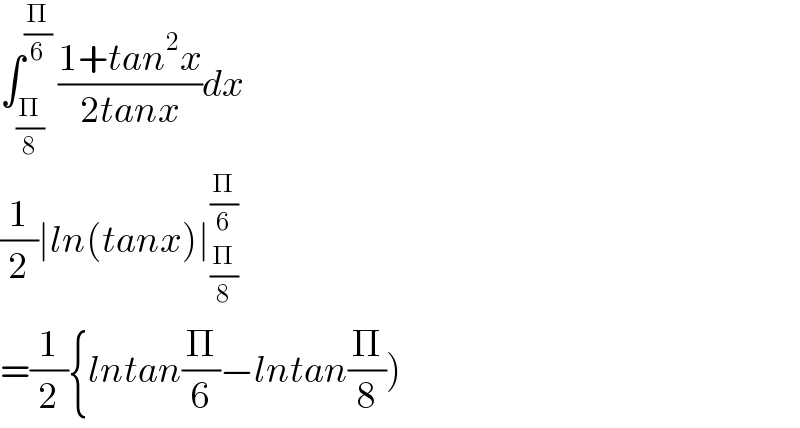 | ||
| ||