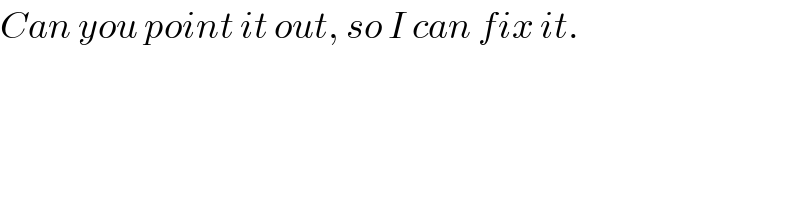calculatef(a)= ∫_(−a) ^a (dx/((t^2 +x^2 )^(3/2) )) with a>0 .


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 33599 by abdo imad last updated on 19/Apr/18

$c a l c u l a t e f (a) = \int_{- a}^{a} \frac{d x}{{(t^{2} + x^{2})}^{\frac{3}{2}}} w i t h a > 0 .$
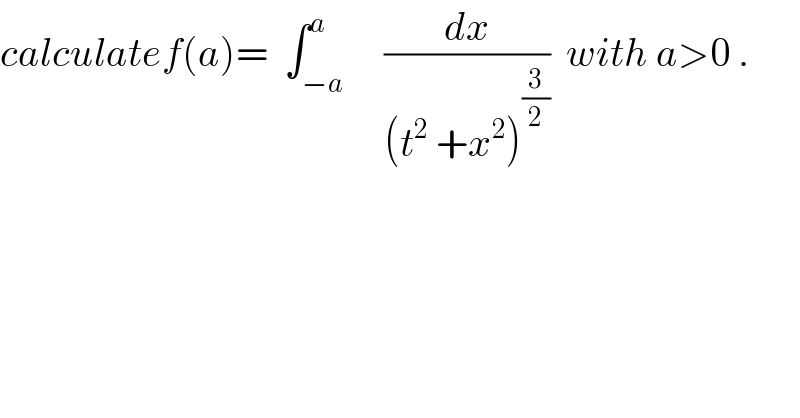
Commented by abdo imad last updated on 20/Apr/18

$c a s e 1 t \neq o c h a n g e m e n t x = t t a n θ g i v e$ $f (a) = \int_{- a r c t a n (\frac{a}{t})}^{a r c t a n (\frac{a}{t})} \frac{1}{{(t^{2} (1 + {t a n}^{2} θ))}^{\frac{3}{2}}} t (1 + {t a n}^{2} θ) d θ$ $= \int_{- a r c t a n (\frac{a}{t})}^{a r c t a n (\frac{a}{t})} \frac{t (1 + {t a n}^{2} θ)}{t^{3} {(1 + {t a n}^{2} θ)}^{\frac{3}{2}}} d θ$ $= \frac{1}{t^{2}} \int_{- a r c t a n (\frac{a}{t})}^{a r c t a n (\frac{a}{t})} \frac{d θ}{{(1 + {t a n}^{2} θ)}^{\frac{1}{2}}}$ $= \frac{2}{t^{2}} \int_{0}^{a r c t a n (\frac{a}{t})} c o s θ d θ = \frac{2}{t^{2}} {[s i n θ]}_{0}^{a r c a n (\frac{a}{t})}$ $= \frac{2}{t^{2}} s i n (a r c t a n (\frac{a}{t})) b u t w e h a v e s i n (a r c t a n u) = \frac{u}{\sqrt{1 + u^{2}}}$ $f (a) = \frac{2}{t^{2}} \frac{\frac{a}{t}}{\sqrt{1 + \frac{a^{2}}{t^{2}}}} = \frac{2 a}{t} \frac{1}{\sqrt{\frac{t^{2} + a^{2}}{t^{2}}}} = \frac{2 a ∣ t ∣}{t \sqrt{a^{2} + t^{2}}}$ $f (a) = \frac{2 a ξ (t)}{\sqrt{t^{2} + a^{2}}} w i t h ξ (t) = 1 i f t > 0 a n d ξ (t) = - 1 i f t < 0$ $c a s e 2 i f t = 0$ $f (a) = \int_{- a}^{a} \frac{d x}{x^{3}} = 0 b e c a u s e x \to x^{3} i s o d d .$
Commented by abdo imad last updated on 20/Apr/18

$e r r o r a t l i n e 7 f (a) = \frac{2 a}{t^{2}} \frac{1}{\sqrt{\frac{t^{2} + a^{2}}{t^{2}}}} = \frac{2 a ∣ t ∣}{t^{2} \sqrt{a^{2} + t^{2}}}$ $= \frac{2 a ξ (t)}{t \sqrt{a^{2} + t^{2}}} .$
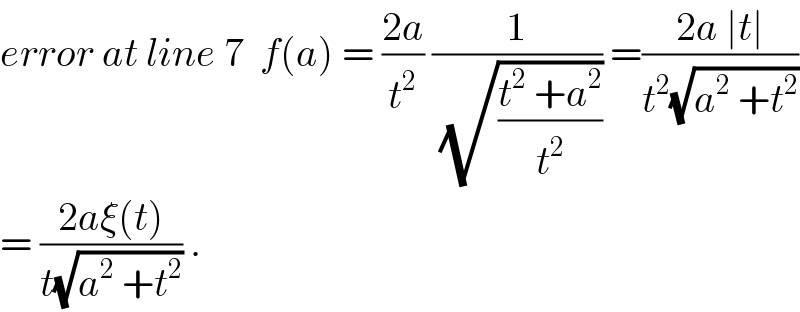
	Answered by alex041103 last updated on 20/Apr/18

	$\int \frac{d x}{{(t^{2} + x^{2})}^{3 / 2}} = \frac{1}{t^{3}} \int \frac{d x}{{(1 + {(\frac{x}{t})}^{2})}^{3 / 2}}$ $L e t u = x / t \Rightarrow d x = t d u$ $\frac{1}{t^{3}} \int \frac{d x}{{(1 + {(\frac{x}{t})}^{2})}^{3 / 2}} = \frac{1}{t^{2}} \int \frac{d u}{{(1 + u^{2})}^{3 / 2}}$ $W e u s e t h e s t a n d a r t t r i g o n o m e t r i c s u b s t i t u t i o n :$ $u = t a n θ d u = {s e c}^{2} θ d θ$ $\frac{1}{t^{2}} \int \frac{d u}{{(1 + u^{2})}^{3 / 2}} = \frac{1}{t^{2}} \int \frac{{s e c}^{2} θ d θ}{{(1 + {t a n}^{2} θ)}^{3 / 2}}$ $A n d {(1 + {t a n}^{2} θ)}^{3 / 2} = {({s e c}^{2} θ)}^{3 / 2} = {s e c}^{3} θ$ $\Rightarrow \frac{1}{t^{2}} \int \frac{{s e c}^{2} θ d θ}{{(1 + {t a n}^{2} θ)}^{3 / 2}} = \frac{1}{t^{2}} \int \frac{{s e c}^{2} θ d θ}{{s e c}^{3} θ} =$ $= \frac{1}{t^{2}} \int c o s θ d θ = \frac{1}{t^{2}} s i n θ$ $u = t a n θ \Rightarrow θ = a r c t a n (u)$ $\Rightarrow \frac{1}{t^{2}} s i n θ = \frac{1}{t^{2}} \frac{u}{\sqrt{1 + u^{2}}} = \frac{u}{t \sqrt{t^{2} + {(t u)}^{2}}} =$ $= \frac{1}{t^{2}} \frac{x}{\sqrt{t^{2} + x^{2}}}$ $\Rightarrow \int_{- a}^{a} \frac{d x}{{(t^{2} + x^{2})}^{3 / 2}} = \frac{1}{t^{2}} {[\frac{x}{\sqrt{t^{2} + x^{2}}}]}_{- a}^{a} =$ $= \frac{2 a}{t^{2} \sqrt{t^{2} + a^{2}}}$ $\Rightarrow \int_{- a}^{a} \frac{d x}{{(t^{2} + x^{2})}^{3 / 2}} = \frac{2 a}{t^{2} \sqrt{t^{2} + a^{2}}}$ $A n y q u e s t i o n s ?$
	Commented by abdo imad last updated on 20/Apr/18

	$y o u h a v e c o m m i t e d a e r r o r s i r a l e x .$
	Commented by alex041103 last updated on 20/May/18

	$C a n y o u p o i n t i t o u t, s o I c a n f i x i t .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum