
Question and Answers Forum
Question Number 77422 by john santu last updated on 06/Jan/20
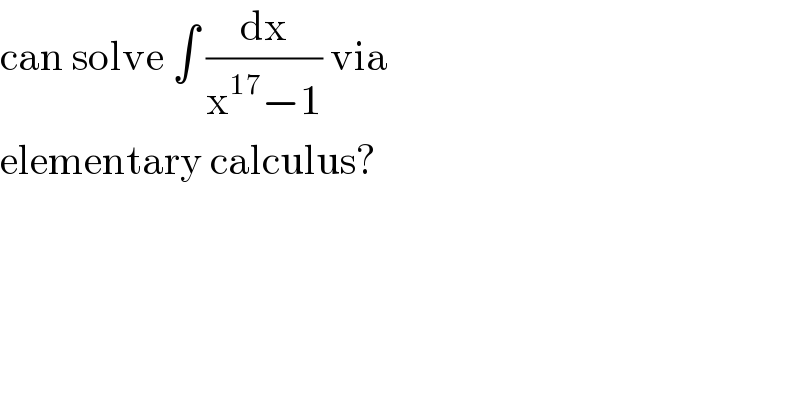
Commented by aliesam last updated on 07/Jan/20
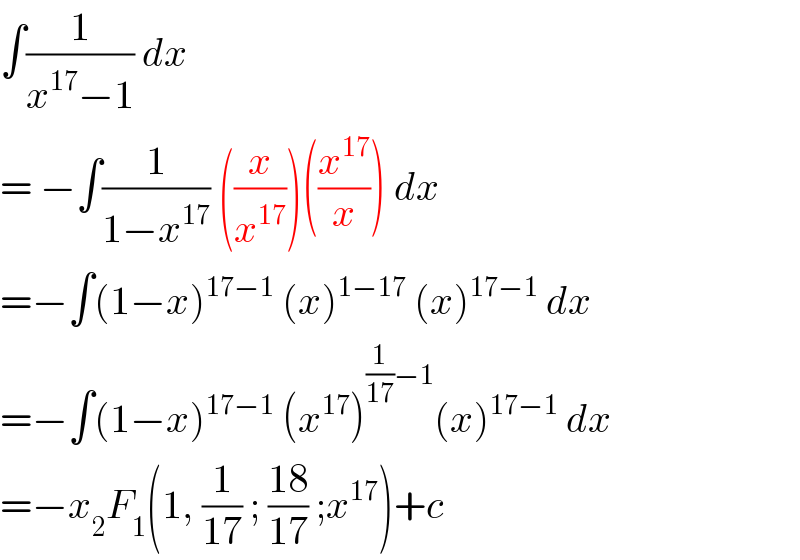
Answered by mind is power last updated on 06/Jan/20
![X^(17) −1=Π_(k=0) ^(16) (x−e^((2ikπ)/(17)) ) ∫(dx/(x^(17) −1))=∫(dx/(Π_(k=0) ^(16) (x−e^((2ikπ)/(17)) )))=∫{Σ_(k=0) ^(16) (a_k /(x−e^((2ikπ)/(17)) ))}dx a_k =(1/(17e^(((2ikπ)/(17)).16) ))=((e^(−((2ikπ)/(17))) )/(17)) ⇒∫(dx/(x^(17) −1))=∫Σ_(k=0) ^(16) (e^((−2ikπ)/(17)) /(17(x−e^((2ikπ)/(17)) ))).dx we can see that Σ_(k=0) ^(16) (e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))=((1/(x−1))+Σ_(k=1) ^8 ((e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))+(e^((−2iπ(17−k))/(17)) /(x−e^((2i(17−k)π)/(17)) )))) =(1/(x−1))+Σ_(k=1) ^8 ((e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))+(e^((2ikπ)/(17)) /(x−e^((−2ikπ)/(17)) )))=(1/(x−1))+Σ_(k=1) ^8 ((2(xcos(((2kπ)/(17)))−cos(((2kπ)/(17)))))/(x^2 −2cos(((2πk)/(17)))x+1)) ∫2((xcos(((2kπ)/(17)))−cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))dx=∫{cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))+((2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))}dx since ∣cos(((2kπ)/(17)))∣<1,∀k∈{1,.....8} ∫cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2xcos(((2πk)/(17)))+1))=cos(((2kπ)/(17)))ln(x^2 −2xcos(((2kπ)/(17)))x+1) ∫((2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))=(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))∫(dx/((x−cos(((2kπ)/(17)))^2 +sin^2 (((2kπ)/(17))))) =(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))arctan((x/(sin(((2kπ)/(17)))))−cot(((2kπ)/(17)))) we Get ∫(dx/(x^(17) −1))=(1/(17))∫{(1/(x−1))+Σ_(k=1) ^8 cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))+(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17)))).(1/(x^2 −2xcos(((2kπ)/(17)))+1))}dx =(1/(17)){ln∣x−1∣+Σ_(k=1) ^8 [cos(((2kπ)/(17)))ln(x^2 −2xcos(((2πk)/(17)))+1)+(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))arctan((x/(sin(((2kπ)/(17)))))−cot(((2kπ)/(17))))]}+c c∈R constant](Q77430.png)
Commented by john santu last updated on 06/Jan/20

| ||
Question and Answers Forum | ||
Question Number 77422 by john santu last updated on 06/Jan/20 | ||
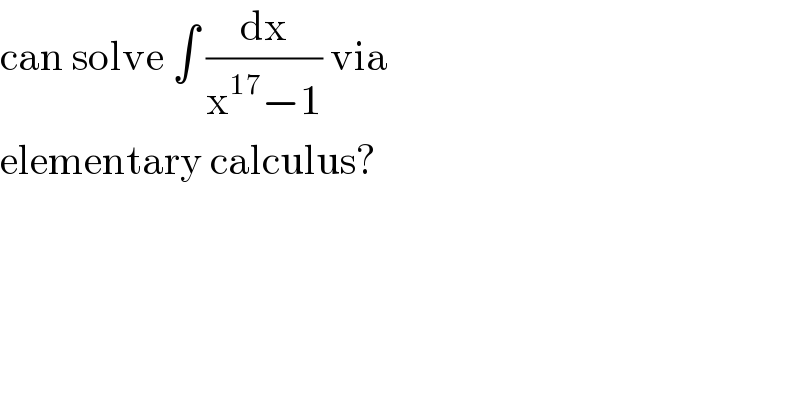 | ||
Commented by aliesam last updated on 07/Jan/20 | ||
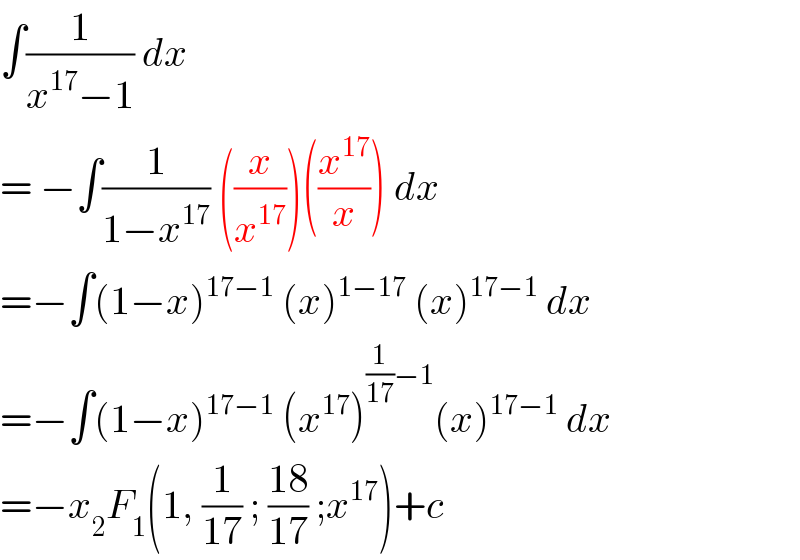 | ||
Answered by mind is power last updated on 06/Jan/20 | ||
![X^(17) −1=Π_(k=0) ^(16) (x−e^((2ikπ)/(17)) ) ∫(dx/(x^(17) −1))=∫(dx/(Π_(k=0) ^(16) (x−e^((2ikπ)/(17)) )))=∫{Σ_(k=0) ^(16) (a_k /(x−e^((2ikπ)/(17)) ))}dx a_k =(1/(17e^(((2ikπ)/(17)).16) ))=((e^(−((2ikπ)/(17))) )/(17)) ⇒∫(dx/(x^(17) −1))=∫Σ_(k=0) ^(16) (e^((−2ikπ)/(17)) /(17(x−e^((2ikπ)/(17)) ))).dx we can see that Σ_(k=0) ^(16) (e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))=((1/(x−1))+Σ_(k=1) ^8 ((e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))+(e^((−2iπ(17−k))/(17)) /(x−e^((2i(17−k)π)/(17)) )))) =(1/(x−1))+Σ_(k=1) ^8 ((e^(−((2ikπ)/(17))) /(x−e^((2ikπ)/(17)) ))+(e^((2ikπ)/(17)) /(x−e^((−2ikπ)/(17)) )))=(1/(x−1))+Σ_(k=1) ^8 ((2(xcos(((2kπ)/(17)))−cos(((2kπ)/(17)))))/(x^2 −2cos(((2πk)/(17)))x+1)) ∫2((xcos(((2kπ)/(17)))−cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))dx=∫{cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))+((2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))}dx since ∣cos(((2kπ)/(17)))∣<1,∀k∈{1,.....8} ∫cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2xcos(((2πk)/(17)))+1))=cos(((2kπ)/(17)))ln(x^2 −2xcos(((2kπ)/(17)))x+1) ∫((2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))=(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))∫(dx/((x−cos(((2kπ)/(17)))^2 +sin^2 (((2kπ)/(17))))) =(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))arctan((x/(sin(((2kπ)/(17)))))−cot(((2kπ)/(17)))) we Get ∫(dx/(x^(17) −1))=(1/(17))∫{(1/(x−1))+Σ_(k=1) ^8 cos(((2kπ)/(17)))((2x−2cos(((2kπ)/(17))))/(x^2 −2cos(((2kπ)/(17)))x+1))+(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17)))).(1/(x^2 −2xcos(((2kπ)/(17)))+1))}dx =(1/(17)){ln∣x−1∣+Σ_(k=1) ^8 [cos(((2kπ)/(17)))ln(x^2 −2xcos(((2πk)/(17)))+1)+(2cos^2 (((2kπ)/(17)))−2cos(((2kπ)/(17))))arctan((x/(sin(((2kπ)/(17)))))−cot(((2kπ)/(17))))]}+c c∈R constant](Q77430.png) | ||
| ||
Commented by john santu last updated on 06/Jan/20 | ||
 | ||