Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 33334 by prof Abdo imad last updated on 14/Apr/18

$$decomposeF\left(x\right)=\frac{x^2}{x^4-1}imsideR\left(x\right)$$$$2)findthevalueof{\int }_2^{+\mathrm{\infty }}\frac{x^2}{x^4-1}.$$

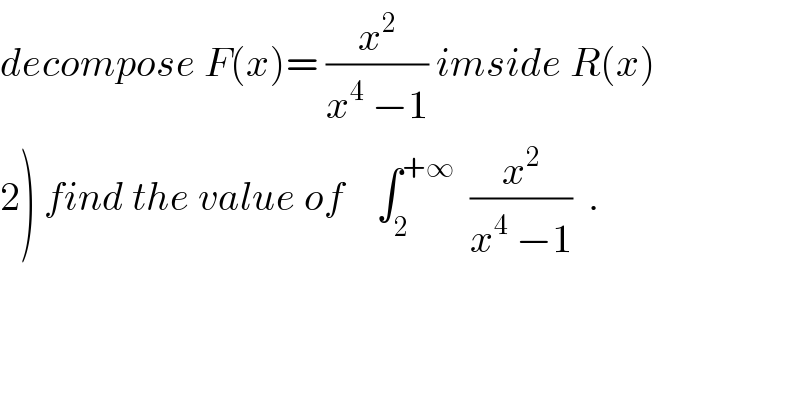
Commented by prof Abdo imad last updated on 15/Apr/18

$$2)findthevalueof{\int }_2^{+\mathrm{\infty }}\frac{x^2}{x^4-1}dx.$$

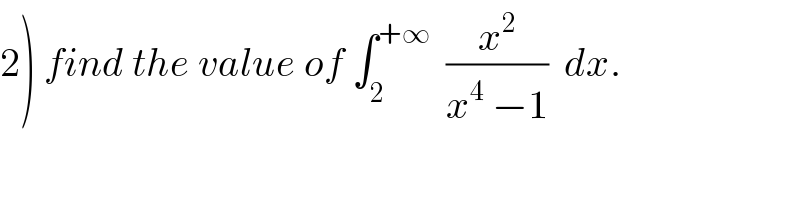
Commented by prof Abdo imad last updated on 18/Apr/18

$$wehaveF\left(x\right)=\frac{x^2}{(x^2-1)(x^2+1)}$$$$=\frac{x^2-1+1}{(x^2-1)(x^2+1)}=\frac{1}{x^2+1}+\frac{1}{(x^2-1)(x^2+1)}$$$$letdecomposeg\left(x\right)=\frac{1}{(x^2-1)(x^2+1)}$$$$g\left(x\right)=\frac{a}{x-1}+\frac{b}{x+1}+\frac{cx+d}{x^2+1}$$$$g(-x)=g\left(x\right)\iff \frac{-a}{x+1}+\frac{-b}{x-1}+\frac{-cx+d}{x^2+1}$$$$=g\left(x\right)\Rightarrow b=-aandc=0\Rightarrow$$$$g\left(x\right)=\frac{a}{x-1}-\frac{a}{x+1}+\frac{d}{x^2+1}$$$$g\left(0\right)=-1=-2a+d\Rightarrow 2a-d=1$$$$g\left(2\right)=\frac{1}{3.5}=\frac{1}{15}=a-\frac{a}{3}+\frac{d}{5}=\frac{2a}{3}+\frac{d}{5}\Rightarrow$$$$1=10a+3d\Rightarrow 10a+3(2a-1)=1\Rightarrow$$$$16a=4\Rightarrow a=\frac{1}{4}andd=\frac{1}{2}-1=-\frac{1}{2}$$$$g\left(x\right)=\frac{1}{4(x-1)}-\frac{1}{4(x+1)}-\frac{1}{2(x^2+1)}\Rightarrow$$$$F\left(x\right)=\frac{1}{x^2+1}+\frac{1}{4(x-1)}-\frac{1}{4(x+1)}-\frac{1}{2(x^2+1)}$$$$F\left(x\right)=\frac{1}{2(x^2+1)}+\frac{1}{4(x-1)}-\frac{1}{4(x+1)}$$

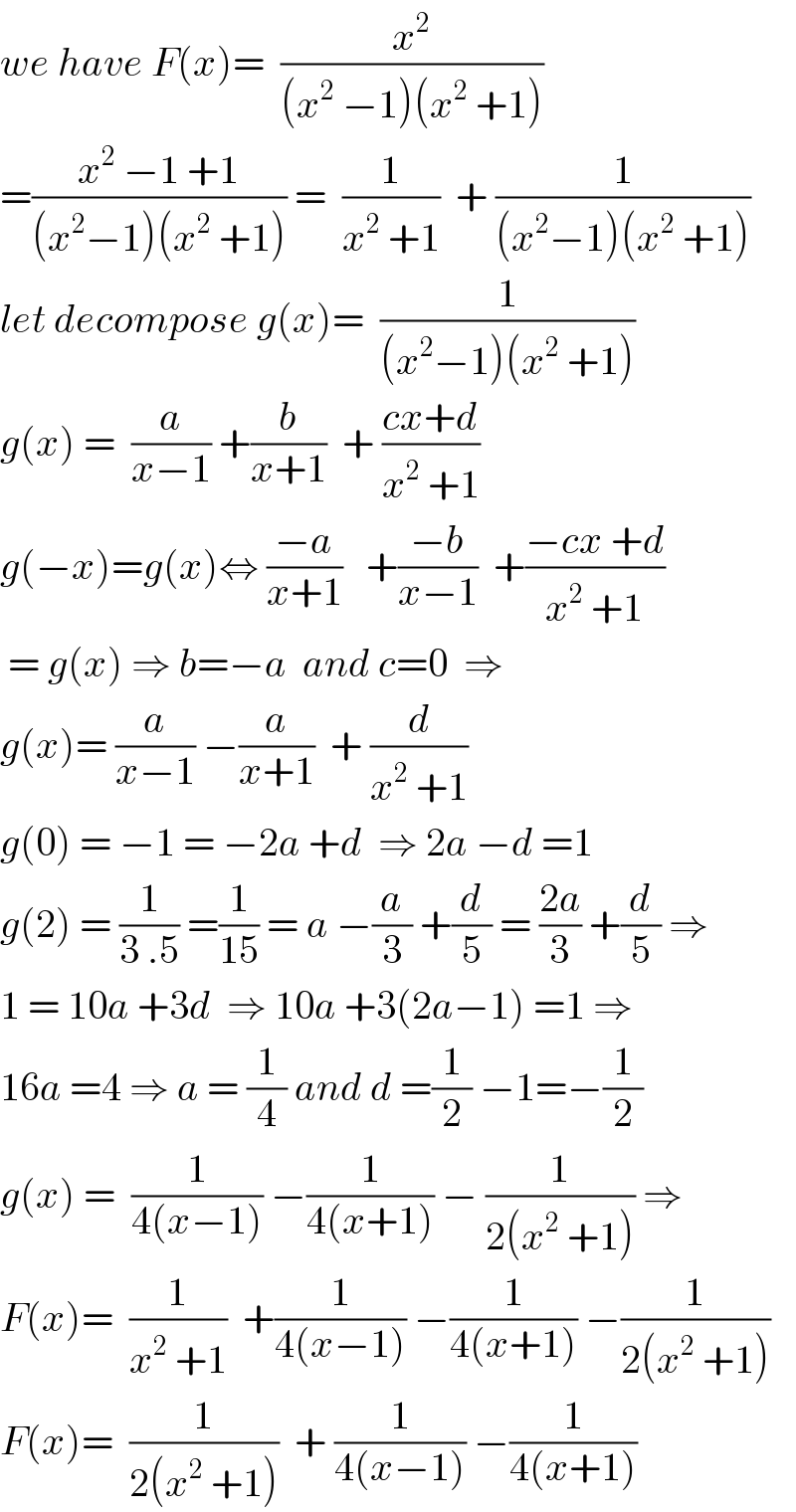
Commented by math khazana by abdo last updated on 19/Apr/18

$${\int }_2^{+\mathrm{\infty }}\frac{x^2}{x^4-1}dx=\frac{1}{2}{\int }_2^{+\mathrm{\infty }}\frac{dx}{1+x^2}+\frac{1}{4}{\int }_2^{+\mathrm{\infty }}(\frac{1}{x-1}-\frac{1}{x+1})dx$$$$=\frac{1}{2}{\left[{arctanx}^{}\right]}_2^{+\mathrm{\infty }}+\frac{1}{4}{[ln\mid \frac{x-1}{x+1}\mid ]}_2^{+\mathrm{\infty }}$$$$=\frac{1}{2}(\frac{\pi }{2}-arctan2)+\frac{1}{4}(-ln\left(\frac{1}{3}\right))$$$$=\frac{\pi }{4}-\frac{1}{2}arctan\left(2\right)+\frac{1}{4}ln\left(3\right).$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com