
Question and Answers Forum
Question Number 116738 by Eric002 last updated on 06/Oct/20
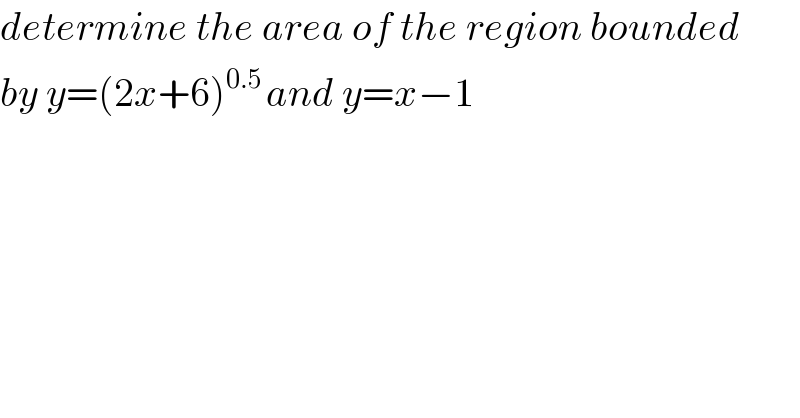
Commented by bobhans last updated on 06/Oct/20

Answered by 1549442205PVT last updated on 06/Oct/20
![Question should be:Calculate the area of region bounded by curve y=(√(2x+6)) ,the line y=x−1 and the Ox We find the intersection of line(d): y=x−1 and the curve C: y=(√(2x+6)) x−1=(√(2x+6))⇔2x+6=x^2 −2x+1(x≥1) ⇔x^2 −4x−5=0 ⇔(x+1)(x−5)=0 ⇔x=5⇒y=4.⇒C∩d=B(5;4) C∩Ox=A(−3;0),d∩Ox=C(1;0).Hence The area of region bounded by C,d and the asix Ox equal to S=∫_(−3) ^( 5) (√(2x+6))dx−∫_1 ^( 5) (x−1)dx Put (√(2x+6))=u⇒2x+6=u^2 ⇒dx=udu ∫(√(2x+6))dx=∫u^2 du=(u^3 /3) ⇒S=(((2x+6)(√(2x+6)))/3)∣_(−3) ^5 −[(x^2 /2)−x]_1 ^5 = =((64)/3)−7.5−0.5=((64)/3)−8=((40)/3) S=((40)/3)](Q116754.png)
| ||
Question and Answers Forum | ||
Question Number 116738 by Eric002 last updated on 06/Oct/20 | ||
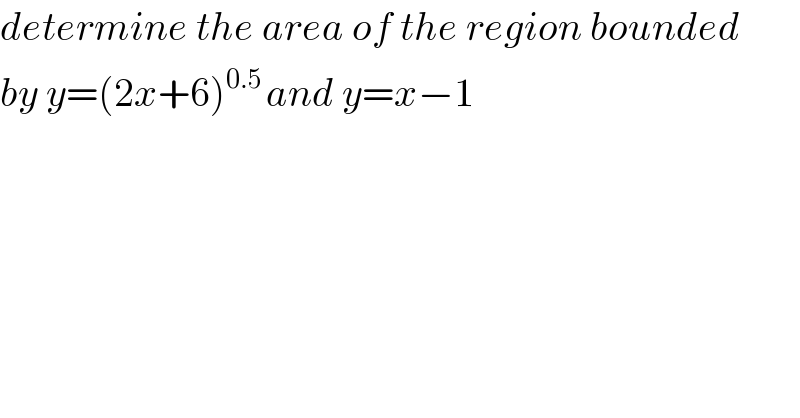 | ||
Commented by bobhans last updated on 06/Oct/20 | ||
 | ||
Answered by 1549442205PVT last updated on 06/Oct/20 | ||
![Question should be:Calculate the area of region bounded by curve y=(√(2x+6)) ,the line y=x−1 and the Ox We find the intersection of line(d): y=x−1 and the curve C: y=(√(2x+6)) x−1=(√(2x+6))⇔2x+6=x^2 −2x+1(x≥1) ⇔x^2 −4x−5=0 ⇔(x+1)(x−5)=0 ⇔x=5⇒y=4.⇒C∩d=B(5;4) C∩Ox=A(−3;0),d∩Ox=C(1;0).Hence The area of region bounded by C,d and the asix Ox equal to S=∫_(−3) ^( 5) (√(2x+6))dx−∫_1 ^( 5) (x−1)dx Put (√(2x+6))=u⇒2x+6=u^2 ⇒dx=udu ∫(√(2x+6))dx=∫u^2 du=(u^3 /3) ⇒S=(((2x+6)(√(2x+6)))/3)∣_(−3) ^5 −[(x^2 /2)−x]_1 ^5 = =((64)/3)−7.5−0.5=((64)/3)−8=((40)/3) S=((40)/3)](Q116754.png) | ||
| ||