
Question and Answers Forum
Question Number 92910 by s.ayeni14@yahoo.com last updated on 09/May/20
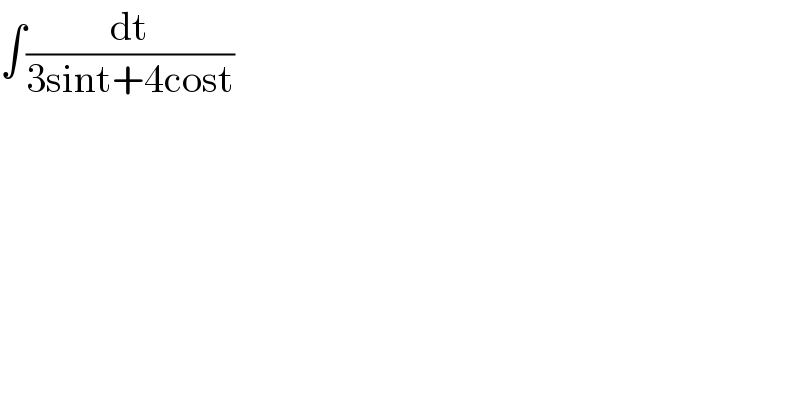
Commented by msup by abdo last updated on 09/May/20
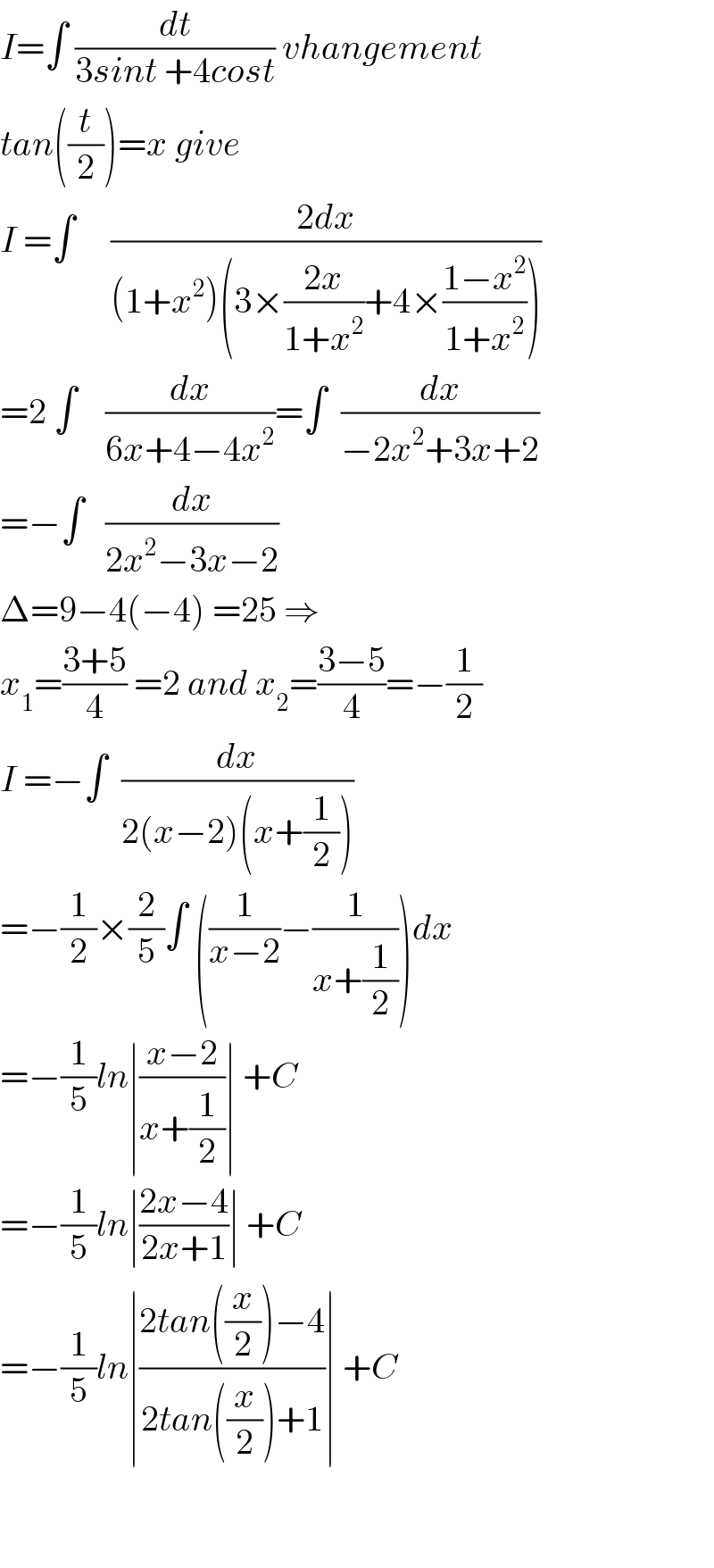
Commented by i jagooll last updated on 10/May/20

Answered by mr W last updated on 09/May/20
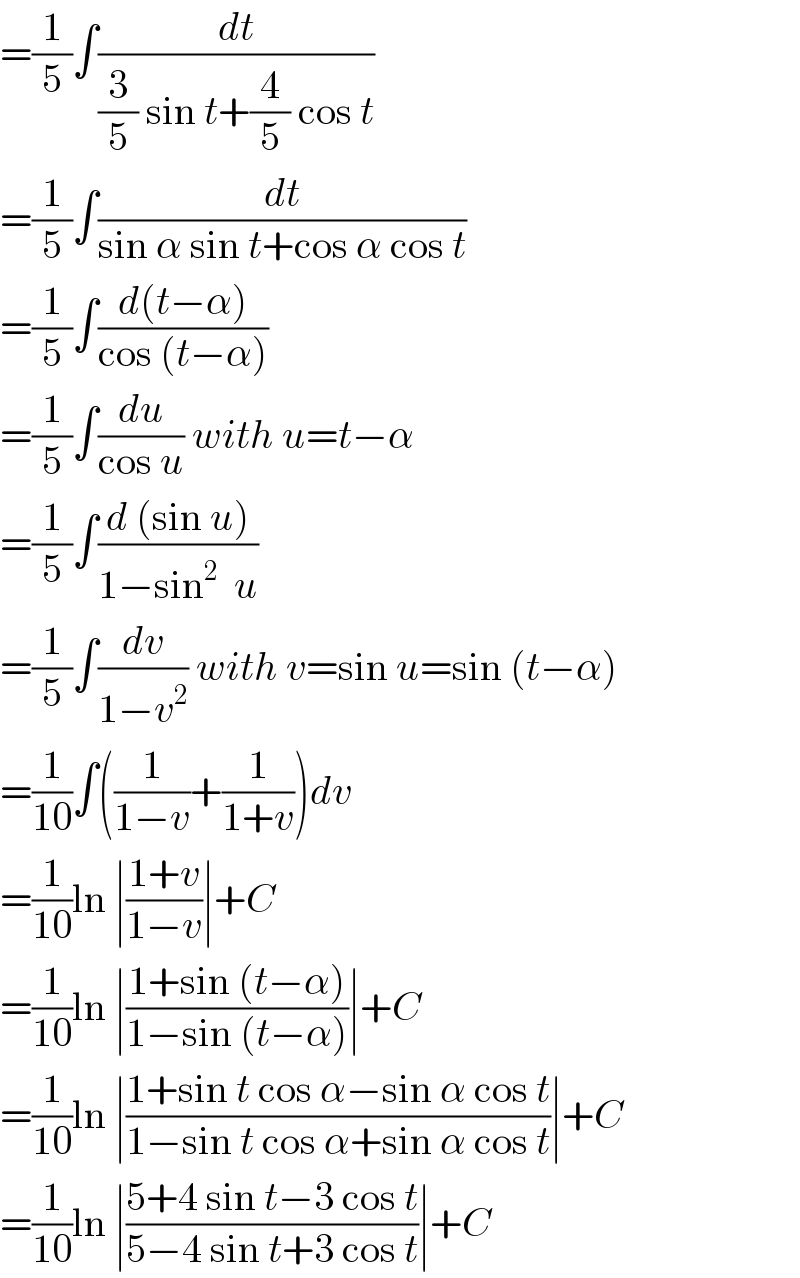
Commented by s.ayeni14@yahoo.com last updated on 09/May/20

Commented by mr W last updated on 09/May/20

Commented by s.ayeni14@yahoo.com last updated on 09/May/20
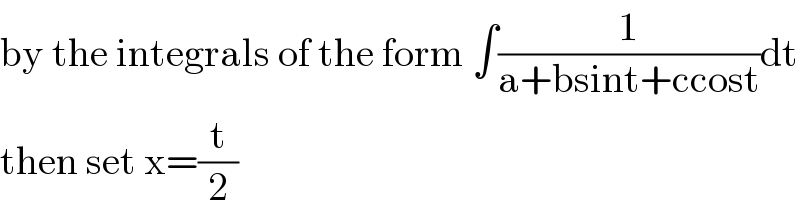
Commented by mr W last updated on 09/May/20

Commented by mr W last updated on 09/May/20
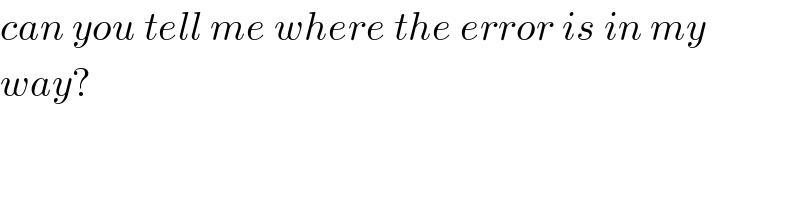
Commented by Ar Brandon last updated on 09/May/20
��It wasn't gonna make a great difference if Mr W used the same method everyone's currently using to arrive at the answer. Thanks Mr W for drawing my attention to your method.��
Commented by Ar Brandon last updated on 09/May/20

Answered by s.ayeni14@yahoo.com last updated on 09/May/20

