Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 83603 by jagoll last updated on 04/Mar/20

$$\int \frac{\mathrm{dx}}{1-2\cos \mathrm{x}}$$

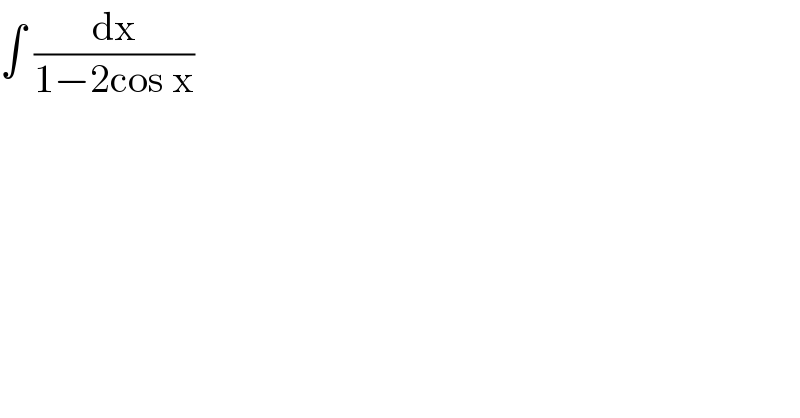
Commented by turbo msup by abdo last updated on 04/Mar/20

$$weusethechangementtan\left(\frac{x}{2}\right)=t$$$$\Rightarrow \int \frac{dx}{1-2cosx}=\int \frac{1}{1-2\frac{1-t^2}{1+t^2}}\times \frac{2dt}{1+t^2}$$$$=2\int \frac{dt}{1+t^2-2+2t^2}=2\int \frac{dt}{3t^2-1}$$$$=2\int \frac{dt}{(\sqrt{3}t-1)(\sqrt{3}+1)}$$$$=\int (\frac{1}{\sqrt{3}t-1}-\frac{1}{\sqrt{3}t+1})dt$$$$=\frac{1}{\sqrt{3}}ln\mid \sqrt{3}t-1\mid -\frac{1}{\sqrt{3}}ln\mid \sqrt{3}t+1\mid +c$$$$=\frac{1}{\sqrt{3}}ln\mid \frac{\sqrt{3}t-1}{\sqrt{3}t+1}\mid +c$$$$=\frac{1}{\sqrt{3}}ln\mid \frac{\sqrt{3}tan\left(\frac{x}{2}\right)-1}{\sqrt{3}tan\left(\frac{x}{2}\right)+1}\mid +C$$

Commented by jagoll last updated on 04/Mar/20

$$\mathrm{thank}\mathrm{you}$$

Commented by mathmax by abdo last updated on 04/Mar/20

$$youarewelcome$$

Commented by niroj last updated on 05/Mar/20

$$\int \frac{\mathrm{dx}}{1-2\cos \mathrm{x}}$$$$\mathrm{let},\cos \mathrm{x}=\frac{1-{\tan }^2\frac{\mathrm{x}}{2}}{1+{\tan }^2\frac{\mathrm{x}}{2}}$$$$=\int \frac{1}{1-2\left(\frac{1-{\tan }^2\frac{\mathrm{x}}{2}}{1+{\tan }^2\frac{\mathrm{x}}{2}}\right)}\mathrm{dx}$$$$=\int \frac{(1+{\tan }^2\frac{\mathrm{x}}{2})\mathrm{dx}}{1+{\tan }^2\frac{\mathrm{x}}{2}-2+{2\tan }^2\frac{\mathrm{x}}{2}}$$$$=\int \frac{{\sec }^2\frac{\mathrm{x}}{2}\mathrm{dx}}{{3\tan }^2\frac{\mathrm{x}}{2}-1}$$$$\mathrm{put}\tan \frac{\mathrm{x}}{2}=\mathrm{t}$$$${\sec }^2\frac{\mathrm{x}}{2}\mathrm{dx}=2\mathrm{dt}$$$$=\int \frac{2\mathrm{dt}}{{3\mathrm{t}}^2-1}=\frac{2}{3}\int \frac{1}{{\mathrm{t}}^2-\frac{1}{3}}\mathrm{dt}$$$$=\frac{2}{3}\int \frac{1}{{\left(\mathrm{t}\right)}^2-{\left(\frac{1}{\sqrt{3}}\right)}^2}\mathrm{dt}$$$$=\frac{2}{3}\left[\frac{1}{2.\frac{1}{\sqrt{3}}}\log \frac{\mathrm{t}-\frac{1}{\sqrt{3}}}{\mathrm{t}+\frac{1}{\sqrt{3}}}\right]+\mathrm{C}$$$$=\frac{2.1}{\frac{3.2}{\sqrt{3}}}\left(\log \frac{\mathrm{t}\sqrt{3}-1}{\mathrm{t}\sqrt{3}+1}\right)+\mathrm{C}$$$$=\frac{1}{\sqrt{3}}\left(\log \frac{\sqrt{3}\tan \frac{\mathrm{x}}{2}-1}{\sqrt{3}\tan \frac{\mathrm{x}}{2}+1}\right)+\mathrm{C}$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com