
Question and Answers Forum
Question Number 103825 by mohammad17 last updated on 17/Jul/20
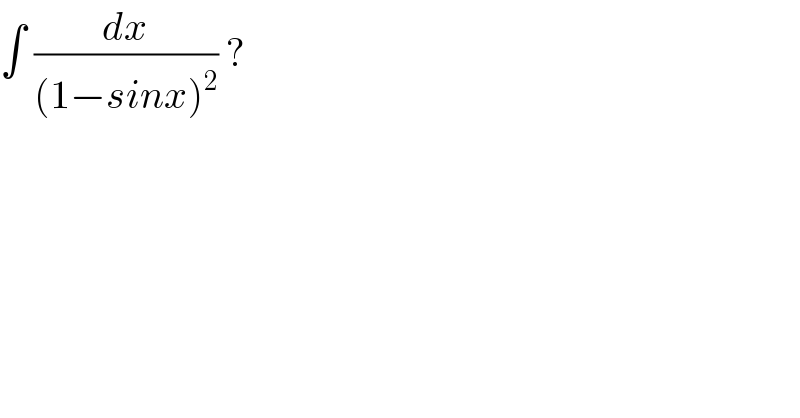
Answered by ~blr237~ last updated on 17/Jul/20
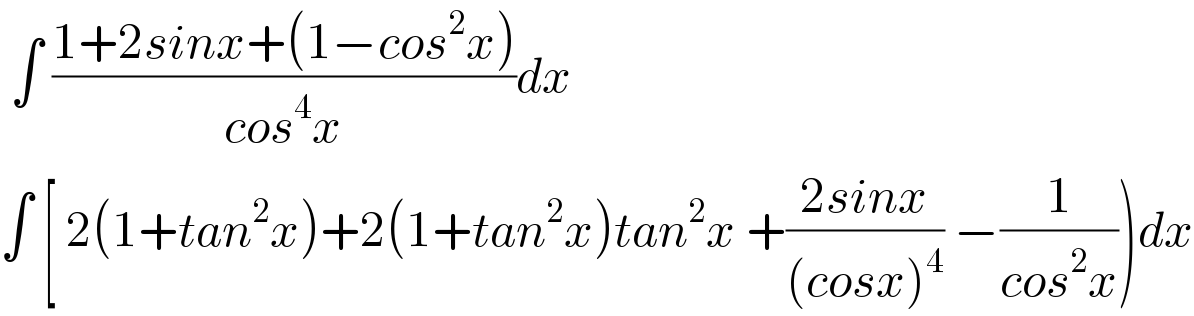
Commented by mohammad17 last updated on 17/Jul/20

Answered by mathmax by abdo last updated on 17/Jul/20

Answered by Dwaipayan Shikari last updated on 17/Jul/20

Commented by mohammad17 last updated on 17/Jul/20

Commented by Dwaipayan Shikari last updated on 17/Jul/20

Commented by Dwaipayan Shikari last updated on 17/Jul/20

Commented by Dwaipayan Shikari last updated on 17/Jul/20
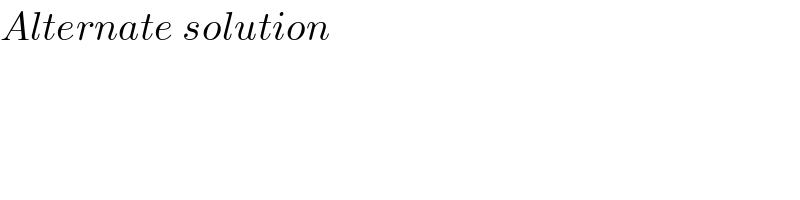
Answered by mathmax by abdo last updated on 17/Jul/20

Commented by mathmax by abdo last updated on 17/Jul/20
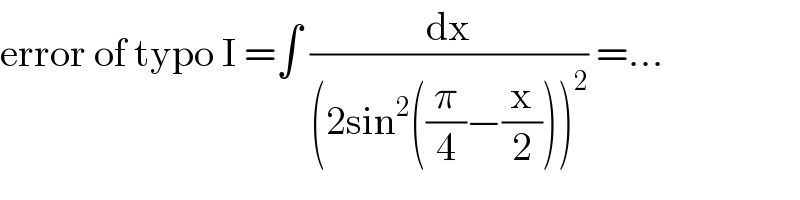
Commented by mathmax by abdo last updated on 17/Jul/20

Commented by mohammad17 last updated on 17/Jul/20

Answered by PRITHWISH SEN 2 last updated on 17/Jul/20

Commented by mohammad17 last updated on 17/Jul/20

Answered by Ar Brandon last updated on 19/Jul/20
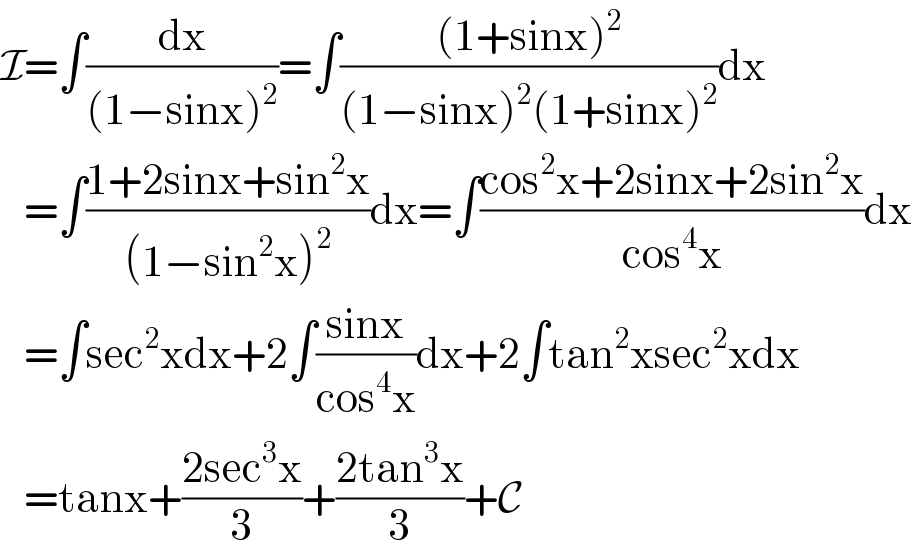
Answered by Her_Majesty last updated on 07/Aug/20

