
Question and Answers Forum
Question Number 129855 by liberty last updated on 20/Jan/21
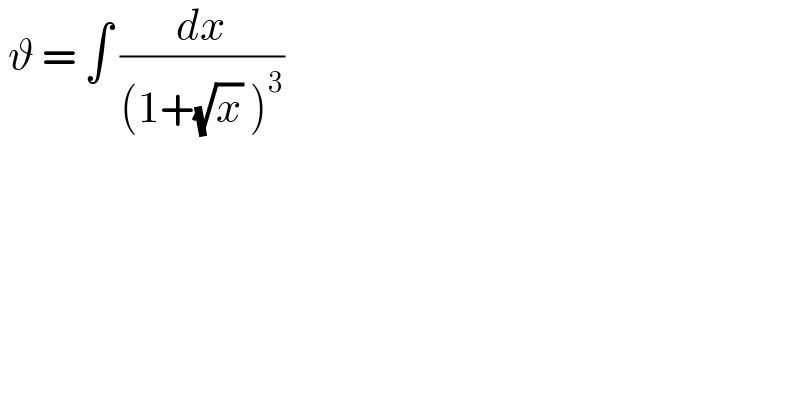
Answered by EDWIN88 last updated on 20/Jan/21
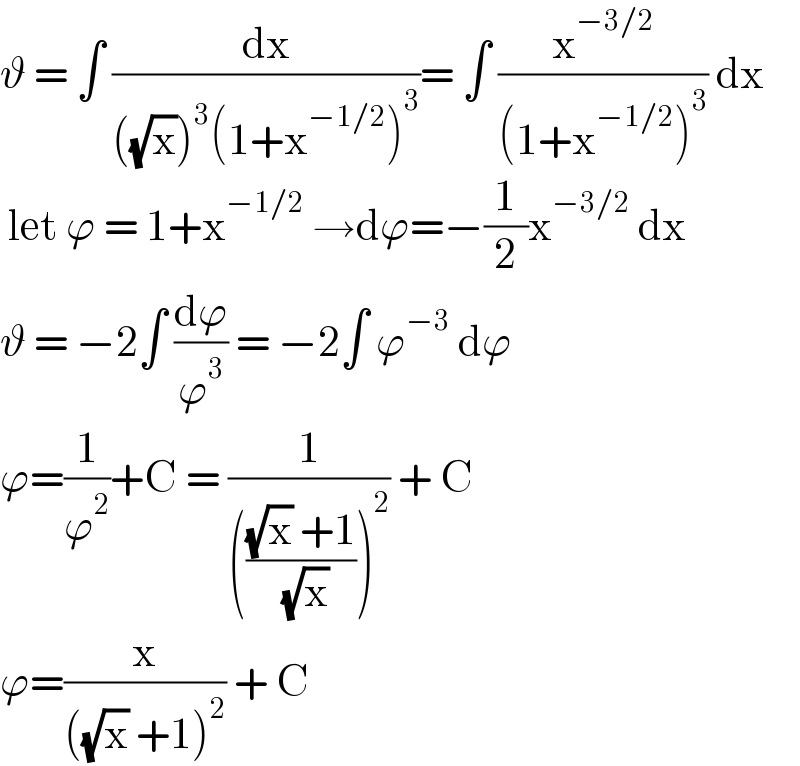
Answered by stelor last updated on 20/Jan/21
![let u =(√x) so, du=(1/(2(√x)))dx = du = (1/(2u))dx v = ∫((2udu)/((1+u)^3 )) where u = (√x) let t = 1+u so, du=dt v =2∫(((t−1))/t^3 )dt where t = u−1= (√x)−1 v=2[∫((1/t^2 )−(1/t^3 ))dt] =2(−(1/t)+(1/(2t^2 )) + c ) v = 2(−(1/( (√x)−1))+(1/(2((√x)−1)^2 )) + c) v= ((3−2(√x))/(((√x)−1)^2 )) + c](Q129894.png)
Commented by bemath last updated on 20/Jan/21
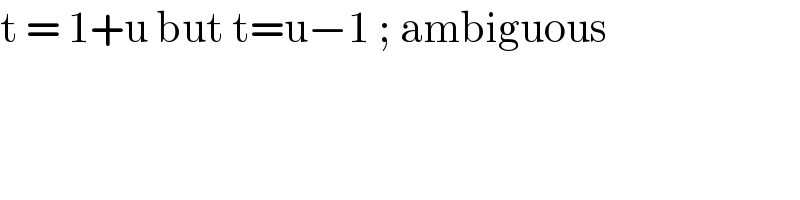
| ||
Question and Answers Forum | ||
Question Number 129855 by liberty last updated on 20/Jan/21 | ||
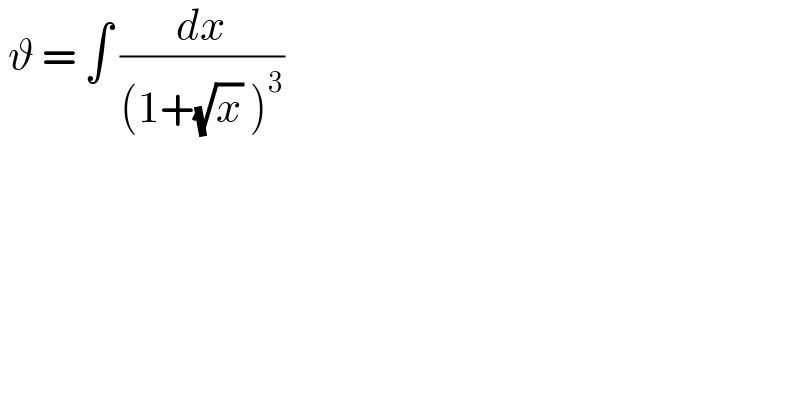 | ||
Answered by EDWIN88 last updated on 20/Jan/21 | ||
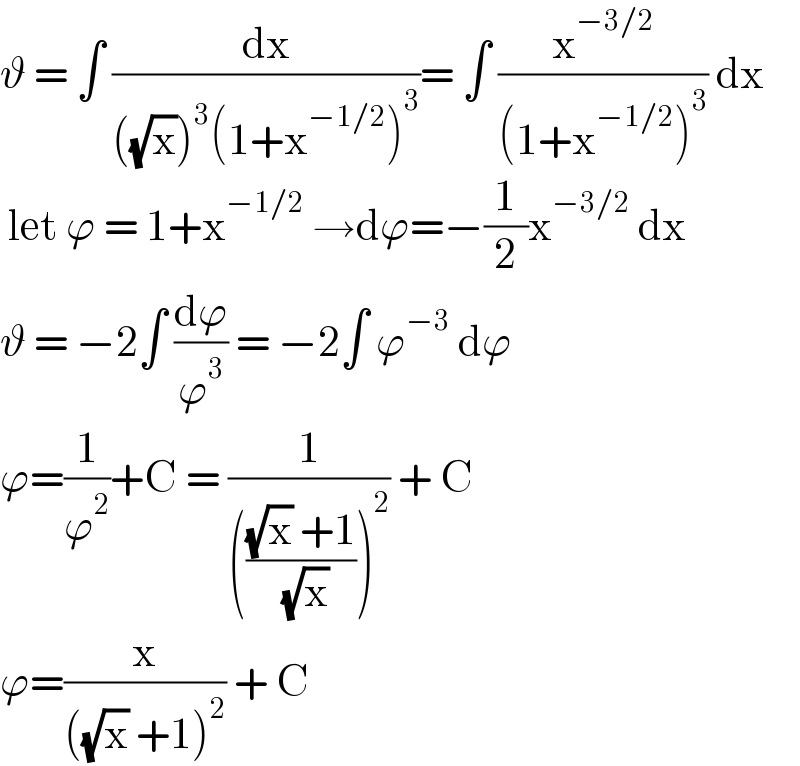 | ||
| ||
Answered by stelor last updated on 20/Jan/21 | ||
![let u =(√x) so, du=(1/(2(√x)))dx = du = (1/(2u))dx v = ∫((2udu)/((1+u)^3 )) where u = (√x) let t = 1+u so, du=dt v =2∫(((t−1))/t^3 )dt where t = u−1= (√x)−1 v=2[∫((1/t^2 )−(1/t^3 ))dt] =2(−(1/t)+(1/(2t^2 )) + c ) v = 2(−(1/( (√x)−1))+(1/(2((√x)−1)^2 )) + c) v= ((3−2(√x))/(((√x)−1)^2 )) + c](Q129894.png) | ||
| ||
Commented by bemath last updated on 20/Jan/21 | ||
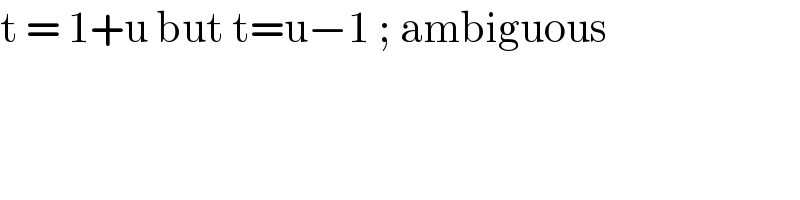 | ||