
Question and Answers Forum
Question Number 164609 by SANOGO last updated on 19/Jan/22
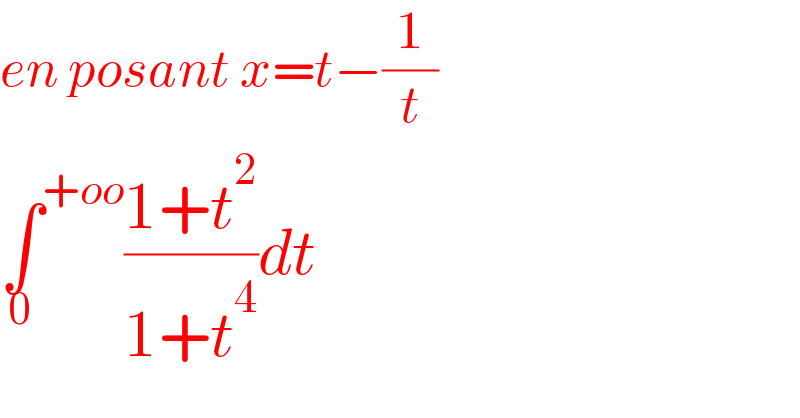
Answered by Mathspace last updated on 19/Jan/22
![I=∫_0 ^∞ ((1+(1/t^2 ))/(t^2 +(1/t^2 ))) dt =∫_0 ^∞ ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt =_(t−(1/t)=x) ∫_(−∞) ^(+∞ ) (dx/(x^2 +2)) =_(x=(√2)y) ∫_(−∞) ^(+∞ ) (((√2)dy)/(2(1+y^2 ))) =((√2)/2)[arctan(y)]_(−∞) ^(+∞) =((√2)/2)((π/2)+(π/2))=((π(√2))/2)](Q164610.png)
Commented by SANOGO last updated on 19/Jan/22
| ||
Question and Answers Forum | ||
Question Number 164609 by SANOGO last updated on 19/Jan/22 | ||
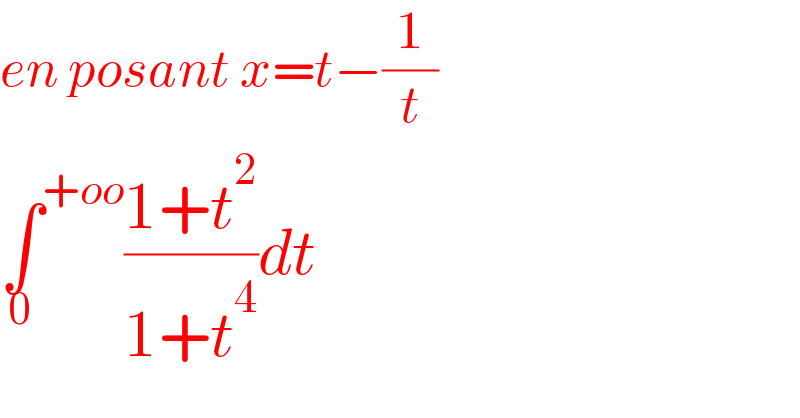 | ||
Answered by Mathspace last updated on 19/Jan/22 | ||
![I=∫_0 ^∞ ((1+(1/t^2 ))/(t^2 +(1/t^2 ))) dt =∫_0 ^∞ ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt =_(t−(1/t)=x) ∫_(−∞) ^(+∞ ) (dx/(x^2 +2)) =_(x=(√2)y) ∫_(−∞) ^(+∞ ) (((√2)dy)/(2(1+y^2 ))) =((√2)/2)[arctan(y)]_(−∞) ^(+∞) =((√2)/2)((π/2)+(π/2))=((π(√2))/2)](Q164610.png) | ||
| ||
Commented by SANOGO last updated on 19/Jan/22 | ||
 | ||