
Question and Answers Forum
Question Number 38123 by maxmathsup by imad last updated on 22/Jun/18

Commented by prof Abdo imad last updated on 22/Jun/18
![changement (√f)=u (u function!) give ∫ (f^′ /(2(√f)(√(1+f))))dx=∫ ((2u^′ u)/(2u(√(1+u^2 ))))dx =∫ (u^′ /(√(1+u^2 )))dx=ln(u +(√(1+u^2 ))) +c =ln((√f) +(√(1+f))) +c 2) we have A_n = ∫_0 ^1 (x^(n/2) /(x(√(1+x^n ))))dx changement x^n =t give x=t^(1/n) and A_n = ∫_0 ^1 (t^(1/2) /(t^((1/n) ) (√(1+t)))) (1/n)t^((1/n) −1) dt =(1/n) ∫_0 ^1 (dt/((√t)(√(1+t)))) =_((√t)=u) (1/n)∫_0 ^1 ((2udu)/(u(√(1+u^2 )))) = (2/n)[ln(u +(√(1+u^2 )))]_0 ^1 =(2/n){ ln(1+(√2))}](Q38189.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18
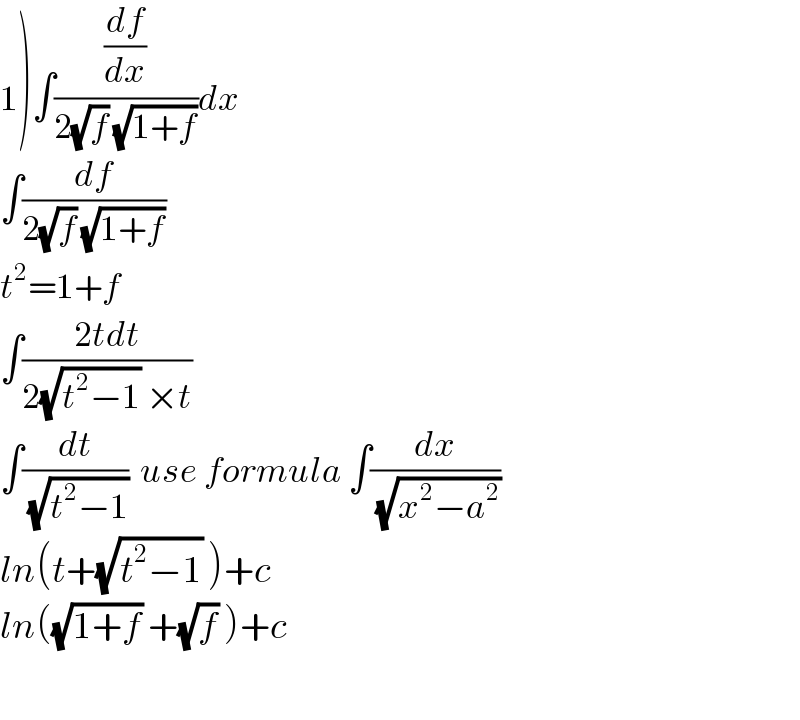
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18

