Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 87052 by lémùst last updated on 02/Apr/20

$$f\left(x\right)={\int }_0^{\pi /2}\frac{{sin}^2\left(t\right)}{1+{xsin}^2\left(t\right)}dt$$

Commented by mathmax by abdo last updated on 02/Apr/20

$$f\left(x\right)={\int }_0^{\frac{\pi }{2}}\frac{{sin}^{2}t}{1+x{sin}^{2}t}dt=\frac{1}{x}{\int }_0^{\frac{\pi }{2}}\frac{{xsin}^{2}t+1-1}{1+{xsin}^{2}t}dt$$$$=\frac{\pi }{2x}-\frac{1}{x}{\int }_0^{\frac{\pi }{2}}\frac{dt}{1+{xsin}^{2}t}[wehave$$$${\int }_0^{\frac{\pi }{2}}\frac{dt}{1+{xsin}^{2}t}={\int }_0^{\frac{\pi }{2}}\frac{dt}{1+x\times \frac{1-cos\left(2t\right)}{2}}$$$${=}_{2x=u}{\int }_0^{\pi }\frac{du}{2(1+x\times \frac{1-cos\left(2u\right)}{2})}={\int }_0^{\pi }\frac{du}{2+x-xcosu}$$$${=}_{tan\left(\frac{u}{2}\right)=z}{\int }_0^{\mathrm{\infty }}\frac{2dz}{(1+z^2)(2+x-x\frac{1-z^2}{1+z^2})}={\int }_0^{\mathrm{\infty }}\frac{2dz}{2+x+(2+x)z^2-x+{xz}^2}$$$$={\int }_0^{\mathrm{\infty }}\frac{2dz}{2+(2+2x)z^2}={\int }_0^{\mathrm{\infty }}\frac{dz}{1+(1+x)z^2}$$$$case11+x>0wedochangementu=\sqrt{1+x}z\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\frac{dz}{1+(1+x)z^2}={\int }_0^{\mathrm{\infty }}\frac{du}{\sqrt{1+x}(1+u^2)}=\frac{1}{\sqrt{1+x}}\times \frac{\pi }{2}\Rightarrow$$$$f\left(x\right)=\frac{\pi }{2x}-\frac{\pi }{2x\sqrt{1+x}}(x>-1andx\ne 0)$$$$case21+x<0\Rightarrow {\int }_0^{\mathrm{\infty }}\frac{dz}{1+(1+x)z^2}={\int }_0^{\mathrm{\infty }}\frac{dz}{1-(-(1+x))z^2}$$$$={\int }_0^{\mathrm{\infty }}\frac{dz}{(1-\sqrt{-1-x}z)(1+\sqrt{-1-x}z)}$$$$=\frac{1}{2}{\int }_0^{\mathrm{\infty }}(\frac{1}{1-\sqrt{-1-x}z}+\frac{1}{1+\sqrt{-1-x}z})$$$$=\frac{1}{2}{\int }_0^{\mathrm{\infty }}(\frac{1}{-\alpha z+1}+\frac{1}{\alpha z+1})dz(\alpha =\sqrt{-1-x})$$$$=\frac{1}{2}{[\frac{1}{\alpha }ln\mid \alpha z+1\mid -\frac{1}{\alpha }ln\mid \alpha z-1\mid ]}_0^{+\mathrm{\infty }}$$$$\frac{1}{2\alpha }{[ln\mid \frac{\alpha z+1}{\alpha z-1}\mid ]}_0^{+\mathrm{\infty }}=0so$$$$f\left(x\right)=\frac{\pi }{2x}-\frac{\pi }{2x\sqrt{1+x}}ifx>-1andx\ne -1$$$$f\left(x\right)=0ifx<-1$$

Commented by lémùst last updated on 02/Apr/20

$$mercibeaucoup$$$$maisjepensequef\left(x\right)=\frac{\pi }{2x}six<-1$$

Commented by mathmax by abdo last updated on 02/Apr/20

$$ouituaraisonjaioublie\frac{\pi }{2x}merci.$$

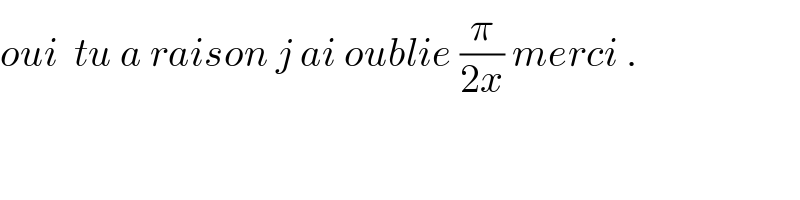
Commented by Ar Brandon last updated on 03/Apr/20

$$genial!!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com