Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 67234 by prof Abdo imad last updated on 24/Aug/19

$$factorisep\left(x\right)=1+x+x^2+x^3+x^5$$$$insideC\left[x\right]andR\left[x\right]$$$$calculatep\left(e^{i\frac{\pi }{5}}\right)andp\left(cos\left(\frac{\pi }{5}\right)\right)$$

Commented by mathmax by abdo last updated on 24/Aug/19

$$sorryp\left(x\right)=1+x+x^2+x^3+x^4$$

Commented by mathmax by abdo last updated on 25/Aug/19

$$1)p\left(x\right)=0\iff 1+x+x^2+x^3+x^4=0\iff 1-x^5=0andx\ne 1$$$$x^5=1letx={re}^{i\theta }\left(e\right)\Rightarrow r^5{e}^{i5\theta }=e^{i\left(2k\pi \right)}\Rightarrow r=1and5\theta =2k\pi \Rightarrow$$$${\theta }_k=\frac{2k\pi }{5}sotherootsare{z}_k=e^{i\left(\frac{2k\pi }{5}\right)}withk\in \left[[1,4]\right]$$$$p\left(x\right)=\prod _{k=1}^4(x-z_k)=\prod _{k=1}^4(x-e^{i\frac{2k\pi }{5}})=(x-e^{i\frac{2\pi }{5}})(x-e^{i\frac{4\pi }{5}})(x-e^{i\frac{6\pi }{5}})(x-e^{i\frac{8\pi }{5}})$$$$but{e}^{i\frac{8\pi }{5}}=e^{i(2\pi -\frac{2\pi }{5})}=e^{-\frac{i2\pi }{5}}and{e}^{i\frac{6\pi }{5}}=e^{-i\frac{4\pi }{5}}\Rightarrow$$$$p\left(x\right)=(x-e^{i\frac{2\pi }{5}})(x-e^{-i\frac{2\pi }{5}})(x-e^{i\frac{4\pi }{5}})(x-e^{-i\frac{4\pi }{5}})$$$$=(x^2-2Re\left(e^{i\frac{2\pi }{5}}\right)x+1)(x^2-2Re\left(e^{i\frac{4\pi }{5}}\right)x+1)isthedecomposition$$$$insideC\left[x\right]$$$$wehavecos\left(\frac{\pi }{5}\right)=\frac{1+\sqrt{5}}{4}\Rightarrow cos\left(\frac{2\pi }{5}\right)=2{cos}^2\left(\frac{\pi }{5}\right)-1$$$$=2{\left(\frac{1+\sqrt{5}}{4}\right)}^2-1=\frac{1}{8}(6+2\sqrt{5})-1=\frac{6+2\sqrt{5}-8}{8}=\frac{-2+2\sqrt{5}}{8}=\frac{\sqrt{5}-1}{4}$$$$cos\left(\frac{4\pi }{5}\right)=cos(\pi -\frac{\pi }{5})=-cos\left(\frac{\pi }{5}\right)\Rightarrow$$$$p\left(x\right)=(x^2-\frac{\sqrt{5}-1}{2}x+1)(x^2+\frac{\sqrt{5}-1}{2}x+1)$$

Commented by mathmax by abdo last updated on 25/Aug/19

$$wehaveforx\ne 1p\left(x\right)=\frac{1-x^5}{1-x}\Rightarrow p\left(e^{i\frac{\pi }{5}}\right)=\frac{1-{\left(e^{\frac{i\pi }{5}}\right)}^5}{1-e^{i\frac{\pi }{5}}}$$$$=\frac{2}{1-e^{\frac{i\pi }{5}}}alsowehavep\left(cos\left(\frac{\pi }{5}\right)\right)=\frac{1-{cos}^5\left(\frac{\pi }{5}\right)}{1-cos\left(\frac{\pi }{5}\right)}$$$$=\frac{1-{\left(\frac{1+\sqrt{5}}{4}\right)}^5}{1-\frac{1+\sqrt{5}}{4}}$$

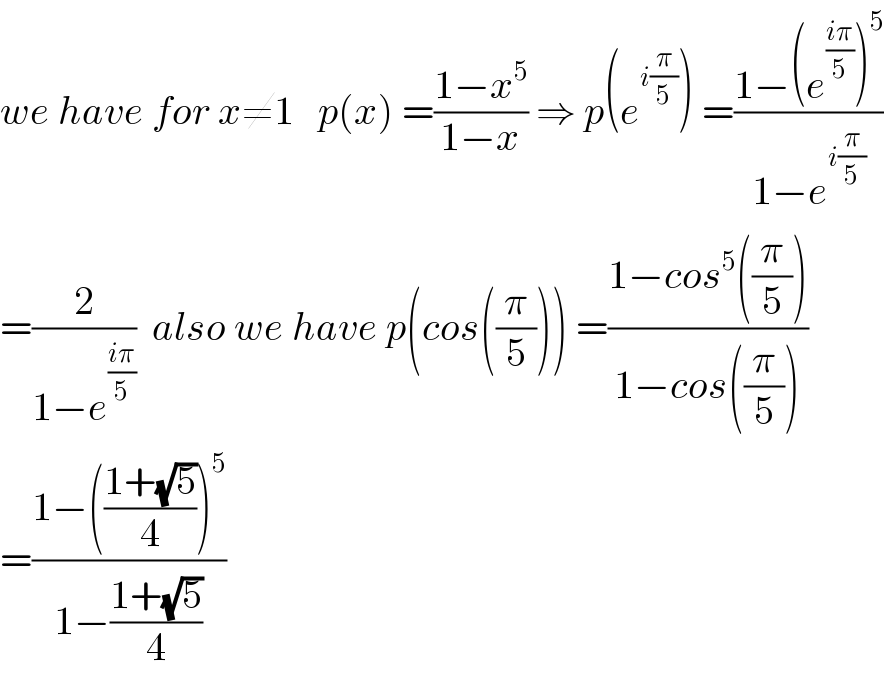
Answered by mind is power last updated on 24/Aug/19

$$p\left(x\right)=1+x+x^2+x^3+x^4?$$$$$$$$$$

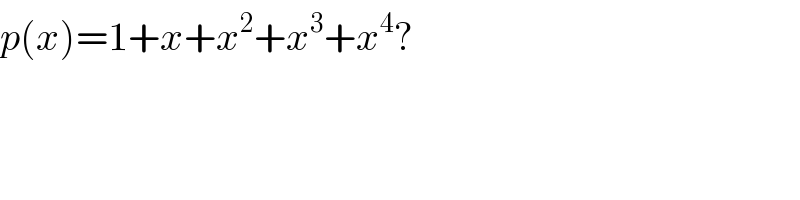
Answered by MJS last updated on 25/Aug/19

$$(x^4+x^3+x^2+x+1)(x-1)=x^5-1$$$$x^5=1$$$$x_0=1$$$$x_1=-\frac{1-\sqrt{5}}{4}+\frac{\sqrt{10+2\sqrt{5}}}{4}\mathrm{i}$$$$x_2=-\frac{1+\sqrt{5}}{4}+\frac{\sqrt{10-2\sqrt{5}}}{4}\mathrm{i}$$$$x_3=-\frac{1+\sqrt{5}}{4}-\frac{\sqrt{10-2\sqrt{5}}}{4}\mathrm{i}$$$$x_4=-\frac{1-\sqrt{5}}{4}-\frac{\sqrt{10+2\sqrt{5}}}{4}\mathrm{i}$$$$\Rightarrow$$$$x^4+x^3+x^2+x+1=$$$$=(x^2+\frac{1-\sqrt{5}}{2}x+1)(x^2+\frac{1+\sqrt{5}}{2}x+1)=$$$$=(x+\frac{1-\sqrt{5}}{4}-\frac{\sqrt{10+2\sqrt{5}}}{4}\mathrm{i})(x+\frac{1-\sqrt{5}}{4}+\frac{\sqrt{10+2\sqrt{5}}}{4}\mathrm{i})(x+\frac{1+\sqrt{5}}{4}-\frac{\sqrt{10-2\sqrt{5}}}{4}\mathrm{i})(x+\frac{1+\sqrt{5}}{4}+\frac{\sqrt{10-2\sqrt{5}}}{4}\mathrm{i})$$$$p\left({\mathrm{e}}^{\mathrm{i}\frac{\pi }{5}}\right)=1+\sqrt{5+2\sqrt{5}}\mathrm{i}$$$$p\left(\cos \frac{\pi }{5}\right)=\frac{67}{32}+\frac{19\sqrt{5}}{32}$$

Commented by mathmax by abdo last updated on 25/Aug/19

$$thankssir.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com