
Question and Answers Forum
Question Number 42394 by abdo.msup.com last updated on 24/Aug/18
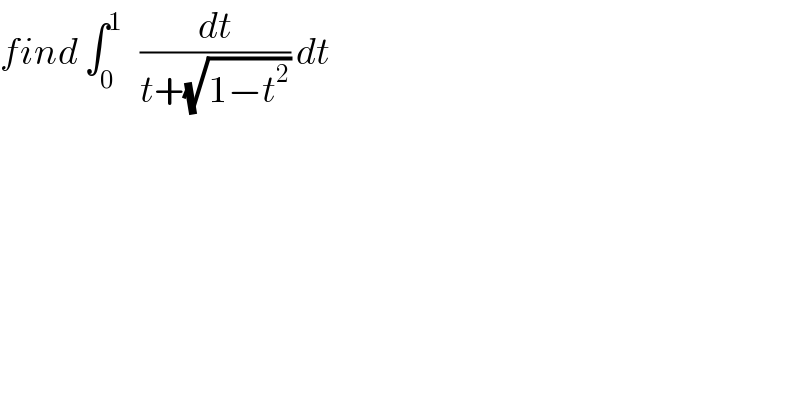
Commented by maxmathsup by imad last updated on 25/Aug/18
![changement t = sinx give I = ∫_0 ^(π/2) ((cosxdx)/(sinx +cosx)) dx = ∫_0 ^(π/2) (dx/(tanx +1)) I =_(tanx =u) ∫_0 ^(+∞) (1/(1+u)) (du/(1+u^2 )) = ∫_0 ^∞ (du/((u+1)(u^2 +1))) let decompose F(u) = (1/((u+1)(u^2 +1))) ⇒F(u) =(a/(u+1)) +((bu +c)/(u^2 +1)) a =lim_(u→−1) (u+1)F(u) =(1/2) lim_(u→+∞) u F(u) =0 =a+b ⇒b =−(1/2) ⇒F(u) =(1/(2(u+1))) +((−(1/2)u +c)/(u^2 +1)) F(0) =1 =(1/2) +c ⇒c =(1/2) ⇒F(u) = (1/(2(u+1))) −(1/2) ((u−1)/(u^2 +1)) ⇒ I = ∫_0 ^∞ F(u)du = (1/2) ∫_0 ^∞ (du/(u+1)) −(1/4) ∫_0 ^∞ ((2u−2)/(u^2 +1))du =[ (1/2)ln∣u+1∣−(1/4)ln(u^2 +1)]_0 ^(+∞) +(1/2) [arctanu]_0 ^(+∞) =(1/2)[ln∣ ((u+1)/(√(u^2 +1)))∣]_0 ^(+∞) +(π/4) =0+(π/4) =(π/4) .](Q42404.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18

| ||
Question and Answers Forum | ||
Question Number 42394 by abdo.msup.com last updated on 24/Aug/18 | ||
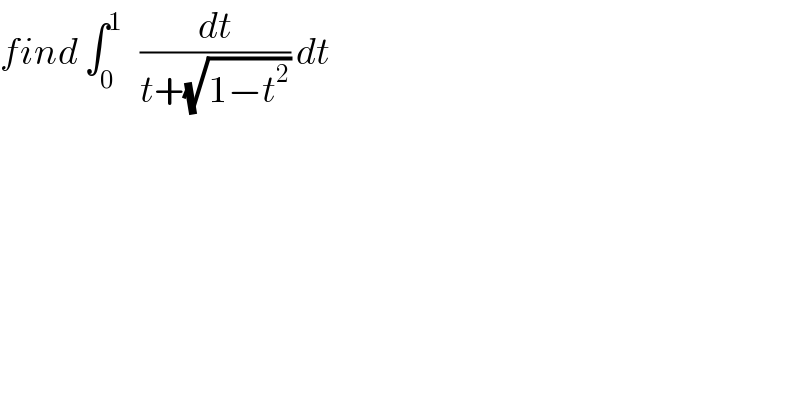 | ||
Commented by maxmathsup by imad last updated on 25/Aug/18 | ||
![changement t = sinx give I = ∫_0 ^(π/2) ((cosxdx)/(sinx +cosx)) dx = ∫_0 ^(π/2) (dx/(tanx +1)) I =_(tanx =u) ∫_0 ^(+∞) (1/(1+u)) (du/(1+u^2 )) = ∫_0 ^∞ (du/((u+1)(u^2 +1))) let decompose F(u) = (1/((u+1)(u^2 +1))) ⇒F(u) =(a/(u+1)) +((bu +c)/(u^2 +1)) a =lim_(u→−1) (u+1)F(u) =(1/2) lim_(u→+∞) u F(u) =0 =a+b ⇒b =−(1/2) ⇒F(u) =(1/(2(u+1))) +((−(1/2)u +c)/(u^2 +1)) F(0) =1 =(1/2) +c ⇒c =(1/2) ⇒F(u) = (1/(2(u+1))) −(1/2) ((u−1)/(u^2 +1)) ⇒ I = ∫_0 ^∞ F(u)du = (1/2) ∫_0 ^∞ (du/(u+1)) −(1/4) ∫_0 ^∞ ((2u−2)/(u^2 +1))du =[ (1/2)ln∣u+1∣−(1/4)ln(u^2 +1)]_0 ^(+∞) +(1/2) [arctanu]_0 ^(+∞) =(1/2)[ln∣ ((u+1)/(√(u^2 +1)))∣]_0 ^(+∞) +(π/4) =0+(π/4) =(π/4) .](Q42404.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18 | ||
 | ||
| ||