find ∫_0 ^1 ((ln(1−x^2 )ln(x))/x^2 )dx prove first the convergence.


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 78270 by msup trace by abdo last updated on 15/Jan/20

$f i n d \int_{0}^{1} \frac{l n (1 - x^{2}) l n (x)}{x^{2}} d x$ $p r o v e f i r s t t h e c o n v e r g e n c e .$
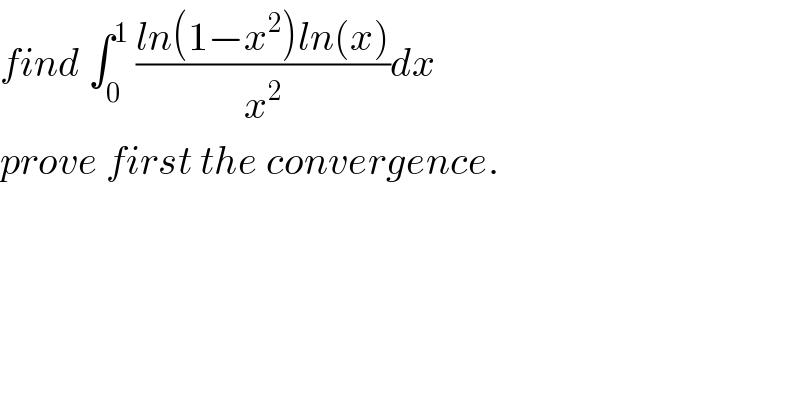
Commented by mathmax by abdo last updated on 15/Jan/20
$let I =∫_0 ^1 ((ln(1−x^2 )ln(x))/x^2 )dx the convergence is assured by sir <mind is power> we have ln^′ (1−u)=−(1/(1−u))=−Σ_(n=0) ^∞ u^n for ∣u∣<1 ⇒ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c (c=0)=−Σ_(n=1) ^∞ (u^n /n) ⇒ ln(1−x^2 ) =−Σ_(n=1) ^∞ (x^(2n) /n) ⇒ ((ln(1−x^2 )ln(x))/x^2 )=−Σ_(n=1) ^∞ (x^(2n−2) /n)ln(x) ⇒I =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(2n−2) ln(x)dx by parts ∫_0 ^1 x^(2n−2) ln(x)dx =[(1/(2n−1))x^(2n−1) ln(x)]_0 ^1 −∫_0 ^1 (1/(2n−1))x^(2n−1) (dx/x) =−(1/(2n−1))∫_0 ^1 x^(2n−2) dx =−(1/((2n−1)^2 ))[x^(2n−1) ]_0 ^1 =((−1)/((2n−1)^2 )) ⇒ I =Σ_(n=1) ^∞ (1/(n(2n−1)^2 )) let decompose F(x)=(1/(x(2x−1)^2 )) F(x)=(a/x) +(b/(2x−1)) +(c/((2x−1)^2 )) a=xF(x)∣_(x=0) =1 c =(2x−1)^2 F(x)∣_(x=(1/2)) =2 ⇒F(x)=(1/x) +(b/(2x−1)) +(2/((2x−1)^2 )) F(1)=1 =1 +b +2 ⇒b=−2 ⇒F(x)=(1/x)−(2/(2x−1)) +(2/((2x−1)^2 )) ⇒ I =Σ_(n=1) ^∞ F(n) =Σ_(n=1) ^∞ ((1/n)−(2/(2n−1))) +2Σ_(n=1) ^∞ (1/((2n−1)^2 )) Σ_(n=1) ^∞ ((1/n)−(2/(2n−1))) =lim s_n with s_n =Σ_(k=1) ^n ((1/k)−(2/(2k−1))) =H_n −2Σ_(k=1) ^n (1/(2k−1)) but Σ_(k=1) ^n (1/(2k−1)) =1 +(1/3) +(1/5) +...+(1/(2n−1)) =1+(1/2) +(1/3) +(1/4) +... +(1/(2n−1)) +(1/(2n)) −(1/2)−(1/4)−...−(1/(2n)) =H_(2n) −(1/2) H_n ⇒ s_n =H_n −2{H_(2n) −(1/2) H_n } =2H_n −2H_(2n) =2( ln(n)+γ +o((1/n))−ln(2n)−γ+o((1/n))) =2( ln((n/(2n))) +o((1/n))) ⇒lim s_n =−2ln(2) let findA= Σ_(n=1) ^∞ (1/((2n−1)^2 )) A =Σ_(n=0) ^∞ (1/((2n+1)^2 )) we have (π^2 /6) =Σ_(n=1) ^∞ (1/n^2 ) =(1/4)Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(1−(1/4))(π^2 /6) =(3/4)×(π^2 /6) =(π^2 /8) ⇒ I =−2ln(2)+2×(π^2 /8) =(π^2 /4)−2ln(2)$
$l e t I = \int_{0}^{1} \frac{l n (1 - x^{2}) l n (x)}{x^{2}} d x t h e c o n v e r g e n c e i s a s s u r e d b y s i r$ $< m i n d i s p o w e r > w e h a v e {l n}^{^{'}} (1 - u) = - \frac{1}{1 - u} = - \sum_{n = 0}^{\infty} u^{n} f o r$ $∣ u ∣< 1 \Rightarrow l n (1 - u) = - \sum_{n = 0}^{\infty} \frac{u^{n + 1}}{n + 1} + c (c = 0) = - \sum_{n = 1}^{\infty} \frac{u^{n}}{n} \Rightarrow$ $l n (1 - x^{2}) = - \sum_{n = 1}^{\infty} \frac{x^{2 n}}{n} \Rightarrow \frac{l n (1 - x^{2}) l n (x)}{x^{2}} = - \sum_{n = 1}^{\infty} \frac{x^{2 n - 2}}{n} l n (x)$ $\Rightarrow I = - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{2 n - 2} l n (x) d x b y p a r t s$ $\int_{0}^{1} x^{2 n - 2} l n (x) d x = {[\frac{1}{2 n - 1} x^{2 n - 1} l n (x)]}_{0}^{1} - \int_{0}^{1} \frac{1}{2 n - 1} x^{2 n - 1} \frac{d x}{x}$ $= - \frac{1}{2 n - 1} \int_{0}^{1} x^{2 n - 2} d x = - \frac{1}{{(2 n - 1)}^{2}} {[x^{2 n - 1}]}_{0}^{1} = \frac{- 1}{{(2 n - 1)}^{2}} \Rightarrow$ $I = \sum_{n = 1}^{\infty} \frac{1}{n {(2 n - 1)}^{2}} l e t d e c o m p o s e F (x) = \frac{1}{x {(2 x - 1)}^{2}}$ $F (x) = \frac{a}{x} + \frac{b}{2 x - 1} + \frac{c}{{(2 x - 1)}^{2}}$ $a = x F (x) ∣_{x = 0} = 1$ $c = {(2 x - 1)}^{2} F (x) ∣_{x = \frac{1}{2}} = 2 \Rightarrow F (x) = \frac{1}{x} + \frac{b}{2 x - 1} + \frac{2}{{(2 x - 1)}^{2}}$ $F (1) = 1 = 1 + b + 2 \Rightarrow b = - 2 \Rightarrow F (x) = \frac{1}{x} - \frac{2}{2 x - 1} + \frac{2}{{(2 x - 1)}^{2}} \Rightarrow$ $I = \sum_{n = 1}^{\infty} F (n) = \sum_{n = 1}^{\infty} (\frac{1}{n} - \frac{2}{2 n - 1}) + 2 \sum_{n = 1}^{\infty} \frac{1}{{(2 n - 1)}^{2}}$ $\sum_{n = 1}^{\infty} (\frac{1}{n} - \frac{2}{2 n - 1}) = l i m s_{n} w i t h s_{n} = \sum_{k = 1}^{n} (\frac{1}{k} - \frac{2}{2 k - 1})$ $= H_{n} - 2 \sum_{k = 1}^{n} \frac{1}{2 k - 1} b u t$ $\sum_{k = 1}^{n} \frac{1}{2 k - 1} = 1 + \frac{1}{3} + \frac{1}{5} + . . . + \frac{1}{2 n - 1}$ $= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . + \frac{1}{2 n - 1} + \frac{1}{2 n} - \frac{1}{2} - \frac{1}{4} - . . . - \frac{1}{2 n}$ $= H_{2 n} - \frac{1}{2} H_{n} \Rightarrow s_{n} = H_{n} - 2 {H_{2 n} - \frac{1}{2} H_{n}}$ $= 2 H_{n} - 2 H_{2 n} = 2 (l n (n) + γ + o (\frac{1}{n}) - l n (2 n) - γ + o (\frac{1}{n}))$ $= 2 (l n (\frac{n}{2 n}) + o (\frac{1}{n})) \Rightarrow l i m s_{n} = - 2 l n (2) l e t f i n d A = \sum_{n = 1}^{\infty} \frac{1}{{(2 n - 1)}^{2}}$ $A = \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} w e h a v e \frac{π^{2}}{6} = \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \frac{1}{4} \sum_{n = 1}^{\infty} \frac{1}{n^{2}} + \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} \Rightarrow$ $\sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} = (1 - \frac{1}{4}) \frac{π^{2}}{6} = \frac{3}{4} \times \frac{π^{2}}{6} = \frac{π^{2}}{8} \Rightarrow$ $I = - 2 l n (2) + 2 \times \frac{π^{2}}{8} = \frac{π^{2}}{4} - 2 l n (2)$
	Answered by mind is power last updated on 15/Jan/20
	$cv in zero ((ln(1−x^2 ))/x^2 )∼1 ((ln(1−x^2 ))/x^2 ).ln(x)∼ln(x) log is integrabl in zero in 1 ((ln(1−x^2 ).ln(x))/x^2 )=g(x) lim_(x→1) (√(1−x )) g(x)=0⇒g(x)=o((1/(√(1−x)))) since (1/(√(1−x))) is integral in 1^− ⇒g also since g is continus ]0,1[ ⇒is integrable ∫_0 ^1 ((ln(1−x^2 )ln(x))/x^2 )dx ln(1−x^2 )=−Σ_(k≥1) (x^(2k) /k) =−∫_0 ^1 Σ_(k≥1) ((x^(2k) ln(x))/k)dx =−Σ_(k≥1) ∫_0 ^1 ((ln(x)x^(2k) )/k)dx u=−ln(x)⇒dx=−e^(−u) du =Σ_(k≥1) ∫_0 ^(+∞) (((−u).(−e^(−u) )e^(−2ku) )/k)du =Σ_(k≥1) ∫_0 ^(+∞) ((ue^(−(1+2k)u) )/k)du,w=(1+2k)u⇒du=(dw/(1+2k)) =Σ_(k≥1) ∫_0 ^(+∞) ((we^(−w) )/(k(1+2k)^2 ))dw =Σ_(k≥1) (1/(k(1+2k)^2 )).∫_0 ^(+∞) we^(−w) dw=Σ_(k≥1) (1/(k(1+2k)^2 )) =Σ((1/k)−(2/((1+2k)^2 ))−(2/((1+2k)))) =Σ_(k≥1) ((2/(2k))−(2/(1+2k)))−2Σ_(k≥1) (1/((1+2k)^2 )) =2{Σ_(k≥1) (((−1)^k )/k)+1}−2((3ζ(2))/4) =2{1−ln(2))−(3/2).(π^2 /6) =2−2ln(2)−(π^2 /4)$
	$cv$ $in zero$ $\frac{\ln (1 - x^{2})}{x^{2}} \sim 1$ $\frac{\ln (1 - x^{2})}{x^{2}} . \ln (x) \sim \ln (x) \log is integrabl in zero$ $in 1$ $\frac{\ln (1 - x^{2}) . \ln (x)}{x^{2}} = g (x)$ $\lim_{x \to 1} \sqrt{1 - x} g (x) = 0 \Rightarrow g (x) = o (\frac{1}{\sqrt{1 - x}})$ $since \frac{1}{\sqrt{1 - x}} is integral in 1^{-} \Rightarrow g also$ $since g is continus] 0, 1 [\Rightarrow is integrable$ $\int_{0}^{1} \frac{\ln (1 - x^{2}) \ln (x)}{x^{2}} dx$ $\ln (1 - x^{2}) = - \sum_{k ⩾ 1} \frac{x^{2 k}}{k}$ $= - \int_{0}^{1} \sum_{k ⩾ 1} \frac{x^{2 k} \ln (x)}{k} dx$ $= - \sum_{k ⩾ 1} \int_{0}^{1} \frac{\ln (x) x^{2 k}}{k} dx$ $u = - \ln (x) \Rightarrow dx = - e^{- u} du$ $= \sum_{k ⩾ 1} \int_{0}^{+ \infty} \frac{(- u) . (- e^{- u}) e^{- 2 ku}}{k} du$ $= \sum_{k ⩾ 1} \int_{0}^{+ \infty} \frac{{ue}^{- (1 + 2 k) u}}{k} du, w = (1 + 2 k) u \Rightarrow du = \frac{dw}{1 + 2 k}$ $= \sum_{k ⩾ 1} \int_{0}^{+ \infty} \frac{{we}^{- w}}{k {(1 + 2 k)}^{2}} dw$ $= \sum_{k ⩾ 1} \frac{1}{k {(1 + 2 k)}^{2}} . \int_{0}^{+ \infty} {we}^{- w} dw = \sum_{k ⩾ 1} \frac{1}{k {(1 + 2 k)}^{2}}$ $= Σ (\frac{1}{k} - \frac{2}{{(1 + 2 k)}^{2}} - \frac{2}{(1 + 2 k)})$ $= \sum_{k ⩾ 1} (\frac{2}{2 k} - \frac{2}{1 + 2 k}) - 2 \sum_{k ⩾ 1} \frac{1}{{(1 + 2 k)}^{2}}$ $= 2 {\sum_{k ⩾ 1} \frac{{(- 1)}^{k}}{k} + 1} - 2 \frac{3 ζ (2)}{4}$ $= 2 {1 - \ln (2)) - \frac{3}{2} . \frac{π^{2}}{6}$ $= 2 - 2 \ln (2) - \frac{π^{2}}{4}$
	Commented by msup trace by abdo last updated on 15/Jan/20

	$t h a n k y o u s i r .$
	Commented by mind is power last updated on 15/Jan/20

	$y^{'} re Welcom$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum