
Question and Answers Forum
Question Number 42803 by maxmathsup by imad last updated on 02/Sep/18

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18
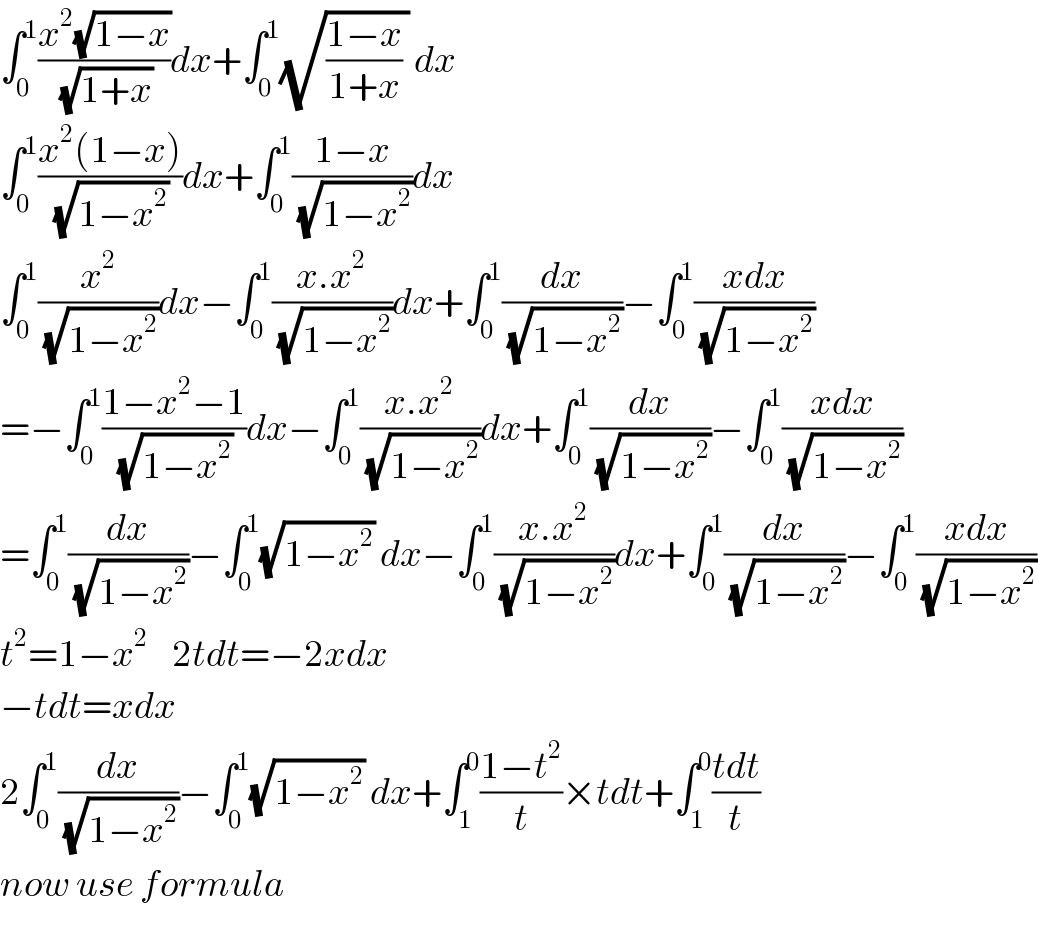
| ||
Question and Answers Forum | ||
Question Number 42803 by maxmathsup by imad last updated on 02/Sep/18 | ||
 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18 | ||
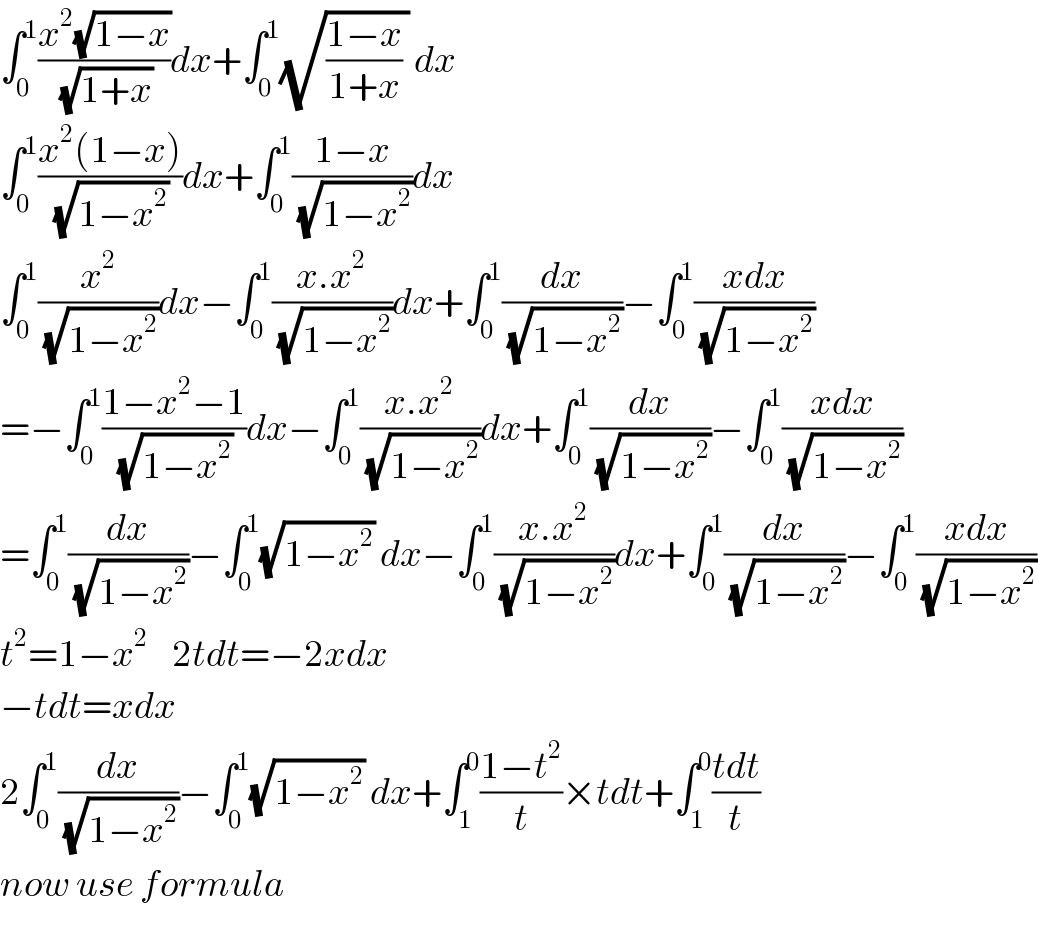 | ||
| ||