
Question and Answers Forum
Question Number 32716 by caravan msup abdo. last updated on 31/Mar/18
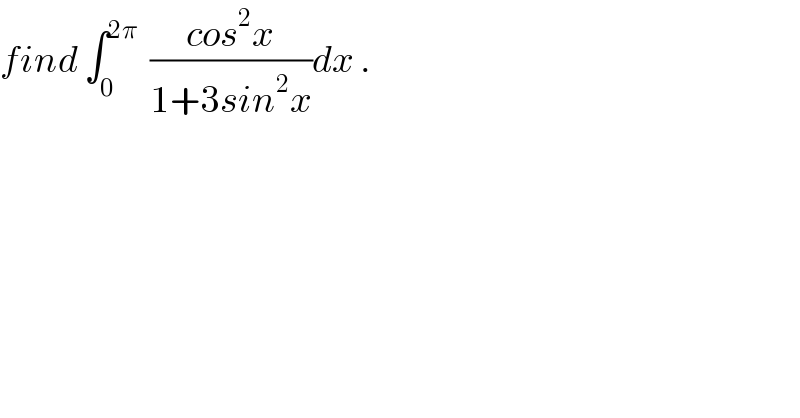
Answered by Joel578 last updated on 02/Apr/18
![I = ∫ (((1 + cos 2x)/2)/(1 + ((3(1 − cos 2x))/2))) dx = ∫ ((1 + cos 2x)/(5 − 3cos 2x)) dx = ∫ ((1 + ((1 − t^2 )/(1 + t^2 )))/(5 − ((3(1 − t^2 ))/(1 + t^2 )))) ((dt/(1 + t^2 ))) → t = tan x = ∫ (2/(2 + 8t^2 ))((dt/(1 + t^2 ))) = ∫ (dt/((1 + 4t^2 )(1 + t^2 ))) = ∫ (4/3)((1/(1 + 4t^2 ))) − (1/3)((1/(1 + t^2 )) )dt = (2/3)tan^(−1) (2t) − (1/3)tan^(−1) (t) = (2/3)tan^(−1) (2tan x) − (x/3) I = 4 [(2/3)tan^(−1) (2tan x) − (x/3)]_0 ^(π/2) = 4[((2/3)tan^(−1) (2tan (π/2)) − (π/6)) − 0] = 4((π/3) − (π/6)) = ((2π)/3)](Q32808.png)
Commented by Joel578 last updated on 02/Apr/18

| ||
Question and Answers Forum | ||
Question Number 32716 by caravan msup abdo. last updated on 31/Mar/18 | ||
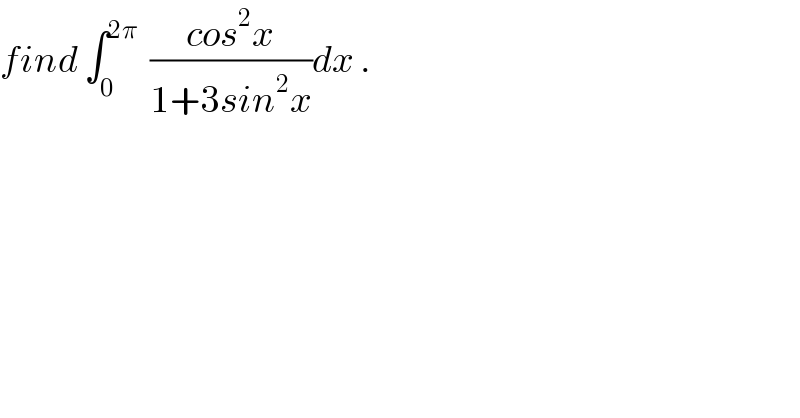 | ||
Answered by Joel578 last updated on 02/Apr/18 | ||
![I = ∫ (((1 + cos 2x)/2)/(1 + ((3(1 − cos 2x))/2))) dx = ∫ ((1 + cos 2x)/(5 − 3cos 2x)) dx = ∫ ((1 + ((1 − t^2 )/(1 + t^2 )))/(5 − ((3(1 − t^2 ))/(1 + t^2 )))) ((dt/(1 + t^2 ))) → t = tan x = ∫ (2/(2 + 8t^2 ))((dt/(1 + t^2 ))) = ∫ (dt/((1 + 4t^2 )(1 + t^2 ))) = ∫ (4/3)((1/(1 + 4t^2 ))) − (1/3)((1/(1 + t^2 )) )dt = (2/3)tan^(−1) (2t) − (1/3)tan^(−1) (t) = (2/3)tan^(−1) (2tan x) − (x/3) I = 4 [(2/3)tan^(−1) (2tan x) − (x/3)]_0 ^(π/2) = 4[((2/3)tan^(−1) (2tan (π/2)) − (π/6)) − 0] = 4((π/3) − (π/6)) = ((2π)/3)](Q32808.png) | ||
| ||
Commented by Joel578 last updated on 02/Apr/18 | ||
 | ||