find ∫_0 ^∞ ((ln(1+ix))/(x^3 +8))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 40580 by maxmathsup by imad last updated on 24/Jul/18

$f i n d \int_{0}^{\infty} \frac{l n (1 + i x)}{x^{3} + 8} d x$
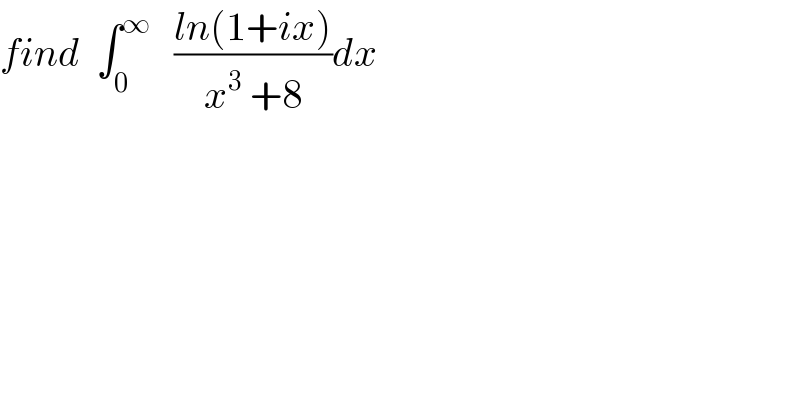
Commented by math khazana by abdo last updated on 28/Jul/18
$we have ∣1+ix∣=(√(1+x^2 ))⇒ 1+ix=(√(1+x^2 ))((1/(√(1+x^2 ))) +i(x/(√(1+x^2 ))))=r e^(iθ) ⇒ r=(√(1+x^2 )) and tanθ =x ⇒θ=arctan(x) ⇒ ln(1+ix)=ln(r)+iθ =(1/2)ln(1+x^2 ) +i arctanx I = (1/2) ∫_0 ^∞ ((ln(1+x^2 ))/(x^3 +8))dx +i ∫_0 ^∞ ((arctanx)/(x^3 +8))dx let f(t) =∫_0 ^∞ ((ln(1+x^2 t))/(x^3 +8))dx we have f^′ (t) =∫_0 ^∞ (x^2 /((1+tx^2 )(x^8 +3)))dx =(1/t)∫_0 ^∞ ((tx^2 +1−1)/((1+tx^2 )(x^3 +8)))dx =(1/t)∫_0 ^∞ (dx/(x^3 +8)) −(1/t)∫_0 ^∞ (dx/((tx^2 +1)(x^3 +8)))let decompose F(x)=(1/(x^3 +8)) =(1/((x+2)(x^2 −2x+4))) =(a/(x+2)) +((bx+c)/(x^2 −2x+4)) a=lim_(x→−2) (x+2)F(x)= (1/(12)) lim_(x→+∞) xF(x)=0=a+b ⇒b=−(1/(12)) F(x)=(1/(12(x+2))) +((−(1/(12))x +c)/(x^2 −2x+4)) F(0) =(1/8) = (1/(24)) +(c/4) ⇒1=(1/3) +2c ⇒2c=(2/3) ⇒ c=(1/3) ⇒ F(x)=(1/(12(x+2))) −(1/(12)) ((x −4)/(x^2 −2x+4)) ∫_0 ^∞ F(x)dx =(1/(12)){ ∫_0 ^∞ (dx/(x+2)) −(1/2)∫_0 ^∞ ((2x−2−6)/(x^2 −2x+4))dx} =(1/(12)){ [ln∣((x+2)/(√(x^2 −2x+4)))∣]_0 ^(+∞) +3 ∫_0 ^∞ (dx/(x^2 −2x+4))} =(1/4) ∫_0 ^∞ (dx/(x^2 −2x+1+3)) =(1/4)∫_0 ^∞ (dx/((x−1)^2 +3)) =_(x−1=(√3)u) (1/4) ∫_(−(1/(√3))) ^∞ (((√3)du)/(3(1+u^2 ))) = ((√3)/(12))[arctanu]_(−(1/(√3))) ^(+∞) =((√3)/(12))((π/2) +arctan((1/(√3))))=((√3)/(12))((π/2) +(π/6))=((√3)/(12)).((2π)/3) =((π(√3))/(18)) = ∫_0 ^∞ (dx/(x^3 +8))$
$w e h a v e ∣ 1 + i x ∣= \sqrt{1 + x^{2}} \Rightarrow$ $1 + i x = \sqrt{1 + x^{2}} (\frac{1}{\sqrt{1 + x^{2}}} + i \frac{x}{\sqrt{1 + x^{2}}}) = r e^{i θ} \Rightarrow$ $r = \sqrt{1 + x^{2}} a n d t a n θ = x \Rightarrow θ = a r c t a n (x) \Rightarrow$ $l n (1 + i x) = l n (r) + i θ = \frac{1}{2} l n (1 + x^{2}) + i a r c t a n x$ $I = \frac{1}{2} \int_{0}^{\infty} \frac{l n (1 + x^{2})}{x^{3} + 8} d x + i \int_{0}^{\infty} \frac{a r c t a n x}{x^{3} + 8} d x$ $l e t f (t) = \int_{0}^{\infty} \frac{l n (1 + x^{2} t)}{x^{3} + 8} d x w e h a v e$ $f^{^{'}} (t) = \int_{0}^{\infty} \frac{x^{2}}{(1 + {t x}^{2}) (x^{8} + 3)} d x$ $= \frac{1}{t} \int_{0}^{\infty} \frac{{t x}^{2} + 1 - 1}{(1 + {t x}^{2}) (x^{3} + 8)} d x$ $= \frac{1}{t} \int_{0}^{\infty} \frac{d x}{x^{3} + 8} - \frac{1}{t} \int_{0}^{\infty} \frac{d x}{({t x}^{2} + 1) (x^{3} + 8)} l e t$ $d e c o m p o s e F (x) = \frac{1}{x^{3} + 8} = \frac{1}{(x + 2) (x^{2} - 2 x + 4)}$ $= \frac{a}{x + 2} + \frac{b x + c}{x^{2} - 2 x + 4}$ $a = {l i m}_{x \to - 2} (x + 2) F (x) = \frac{1}{12}$ ${l i m}_{x \to + \infty} x F (x) = 0 = a + b \Rightarrow b = - \frac{1}{12}$ $F (x) = \frac{1}{12 (x + 2)} + \frac{- \frac{1}{12} x + c}{x^{2} - 2 x + 4}$ $F (0) = \frac{1}{8} = \frac{1}{24} + \frac{c}{4} \Rightarrow 1 = \frac{1}{3} + 2 c \Rightarrow 2 c = \frac{2}{3} \Rightarrow$ $c = \frac{1}{3} \Rightarrow F (x) = \frac{1}{12 (x + 2)} - \frac{1}{12} \frac{x - 4}{x^{2} - 2 x + 4}$ $\int_{0}^{\infty} F (x) d x = \frac{1}{12} {\int_{0}^{\infty} \frac{d x}{x + 2} - \frac{1}{2} \int_{0}^{\infty} \frac{2 x - 2 - 6}{x^{2} - 2 x + 4} d x}$ $= \frac{1}{12} {{[l n ∣ \frac{x + 2}{\sqrt{x^{2} - 2 x + 4}} ∣]}_{0}^{+ \infty} + 3 \int_{0}^{\infty} \frac{d x}{x^{2} - 2 x + 4}}$ $= \frac{1}{4} \int_{0}^{\infty} \frac{d x}{x^{2} - 2 x + 1 + 3} = \frac{1}{4} \int_{0}^{\infty} \frac{d x}{{(x - 1)}^{2} + 3}$ $=_{x - 1 = \sqrt{3} u} \frac{1}{4} \int_{- \frac{1}{\sqrt{3}}}^{\infty} \frac{\sqrt{3} d u}{3 (1 + u^{2})} = \frac{\sqrt{3}}{12} {[a r c t a n u]}_{- \frac{1}{\sqrt{3}}}^{+ \infty}$ $= \frac{\sqrt{3}}{12} (\frac{π}{2} + a r c t a n (\frac{1}{\sqrt{3}})) = \frac{\sqrt{3}}{12} (\frac{π}{2} + \frac{π}{6}) = \frac{\sqrt{3}}{12} . \frac{2 π}{3}$ $= \frac{π \sqrt{3}}{18} = \int_{0}^{\infty} \frac{d x}{x^{3} + 8}$
Commented by math khazana by abdo last updated on 28/Jul/18

$l e t d e c o m p o s e G (t) = \frac{1}{({t x}^{2} + 1) (x^{3} + 8)}$ $G (t) = \frac{1}{({t x}^{2} + 1) (x + 2) (x^{2} - 2 x + 4)}$ $= \frac{a}{x + 2} + \frac{b x + c}{{t x}^{2} + 1} + \frac{d x + e}{x^{2} - 2 x + 4}$ $a = {l i m}_{x \to - 2} (x + 2) G (x) = \frac{1}{12 (4 t + 1)}$ ${l i m}_{x \to + \infty} x G (x) = 0 = a + \frac{b}{t} + d \Rightarrow a t + b + d t = 0$ $. . . . b e c o n t i n u e d . . .$
Commented by math khazana by abdo last updated on 28/Jul/18

$l e t J = \int_{0}^{\infty} \frac{a r c t a n x}{x^{3} + 8} d x c h a n g e m e n t$ $x = 2 t g i v e J = 2 \int_{0}^{\infty} \frac{a r c t a n (2 t)}{8 (t^{3} + 1)} d t$ $= \frac{1}{4} \int_{0}^{\infty} \frac{a r c t a n (2 t)}{t^{3} + 1} d t l e t$ $w (x) = \int_{0}^{\infty} \frac{a r c t a n (x t)}{t^{3} + 1} d t$ $w^{^{'}} (x) = \int_{0}^{\infty} \frac{t}{(1 + x^{2} t^{2}) (t^{3} + 1)} d t l e t d e c o m p o s e$ $H (t) = \frac{t}{(x^{2} t^{2} + 1) (t^{3} + 1)}$ $H (t) = \frac{t}{(x^{2} t^{2} + 1) (t + 1) (t^{2} - t + 1)}$ $= \frac{a}{t + 1} + \frac{b t + c}{x^{2} t^{2} + 1} + \frac{d t + e}{t^{2} - t + 1}$ $a = {l i m}_{t \to - 1} (t + 1) H (t) = \frac{- 1}{3 (t^{2} + 1)}$ ${l i m}_{t \to + \infty} t H (t) = a + \frac{b}{x^{2}} + d = 0 \Rightarrow {a x}^{2} + b + {d x}^{2} = 0$ $. . . . b e c o n t i n u e d . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum