
Question and Answers Forum
Question Number 40141 by maxmathsup by imad last updated on 16/Jul/18
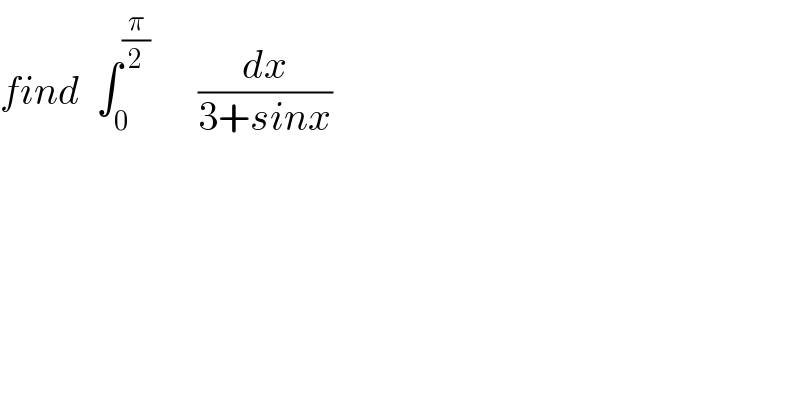
Commented by maxmathsup by imad last updated on 19/Jul/18
![let I = ∫_0 ^(π/2) (dx/(3+sinx)) changement tan((x/2))=t give I = ∫_0 ^1 (1/(3+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2 ∫_0 ^1 (dt/(3+3t^2 +2t)) =2 ∫_0 ^1 (dt/(3t^2 +2t +3)) but 3t^2 +2t +3 =3(t^2 +(2/3)t +1) =3( t^2 +(2/3)t +(1/9) +1−(1/9)) =3{ (t+(1/3))^2 +(8/9)} ⇒ I =(2/3) ∫_0 ^1 (dt/((t+(1/3))^2 +(8/9))) =_(t+(1/3)=((2(√2))/3)u) (2/3) ∫_(1/(2(√2))) ^(√2) (1/((8/9)(1+u^2 ))) ((2(√2))/3)du =((4(√2))/9) (9/8) ∫_(1/(2(√2))) ^(√2) (du/(1+u^2 )) =((√2)/2) [arctanu]_(1/(√2)) ^(√2) ⇒ I = ((√2)/2){ arctan((√2))−arctan((1/(√2)))}.](Q40343.png)
| ||
Question and Answers Forum | ||
Question Number 40141 by maxmathsup by imad last updated on 16/Jul/18 | ||
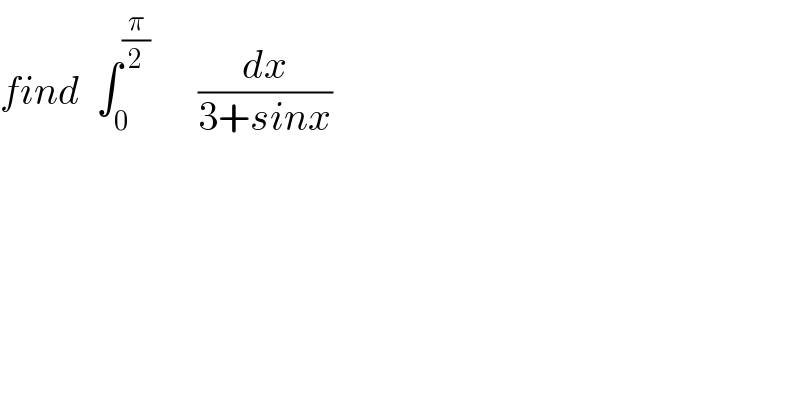 | ||
Commented by maxmathsup by imad last updated on 19/Jul/18 | ||
![let I = ∫_0 ^(π/2) (dx/(3+sinx)) changement tan((x/2))=t give I = ∫_0 ^1 (1/(3+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2 ∫_0 ^1 (dt/(3+3t^2 +2t)) =2 ∫_0 ^1 (dt/(3t^2 +2t +3)) but 3t^2 +2t +3 =3(t^2 +(2/3)t +1) =3( t^2 +(2/3)t +(1/9) +1−(1/9)) =3{ (t+(1/3))^2 +(8/9)} ⇒ I =(2/3) ∫_0 ^1 (dt/((t+(1/3))^2 +(8/9))) =_(t+(1/3)=((2(√2))/3)u) (2/3) ∫_(1/(2(√2))) ^(√2) (1/((8/9)(1+u^2 ))) ((2(√2))/3)du =((4(√2))/9) (9/8) ∫_(1/(2(√2))) ^(√2) (du/(1+u^2 )) =((√2)/2) [arctanu]_(1/(√2)) ^(√2) ⇒ I = ((√2)/2){ arctan((√2))−arctan((1/(√2)))}.](Q40343.png) | ||