
Question and Answers Forum
Question Number 27502 by abdo imad last updated on 07/Jan/18
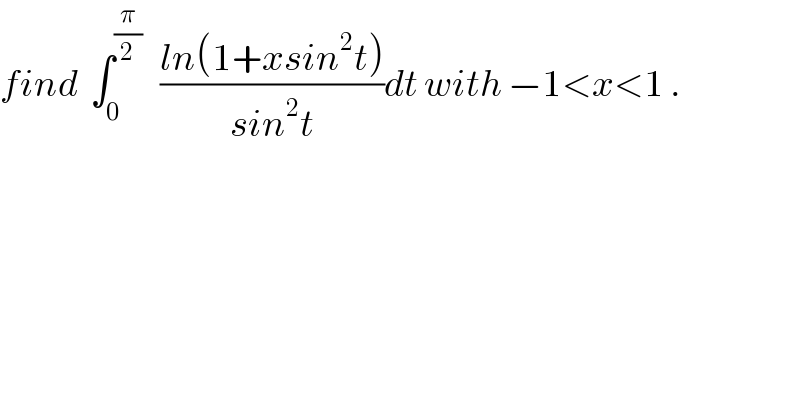
Commented by abdo imad last updated on 09/Jan/18
![let put f(x)= ∫_0 ^(π/2) ((ln(1+xsin^2 t))/(sin^2 t))dt after verifying that f is derivable on ]−1,1[ we have f^, (x)= ∫_0 ^(π/2) (dt/(1+xsin^2 t)) because of /xsin^2 t/<1 f^′ (x)= ∫_0 ^(π/2) ( Σ_(n=0) ^∝ (−1)^n x^n sin^(2n) t)dt =Σ_(n=0) ^∝ (−1)^n x^n ∫_0 ^(π/2) sin^(2n) tdt= Σ_(n=0) ^∝ (−1)^n W_n x^n with W_n = ∫_0 ^(π/2) sin^(2n) tdt and the value of W_n is known (walliss integral) f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n x^(n+1) +λ λ=f(0)=0⇒ f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n .x^(n+1) .](Q27573.png)
| ||
Question and Answers Forum | ||
Question Number 27502 by abdo imad last updated on 07/Jan/18 | ||
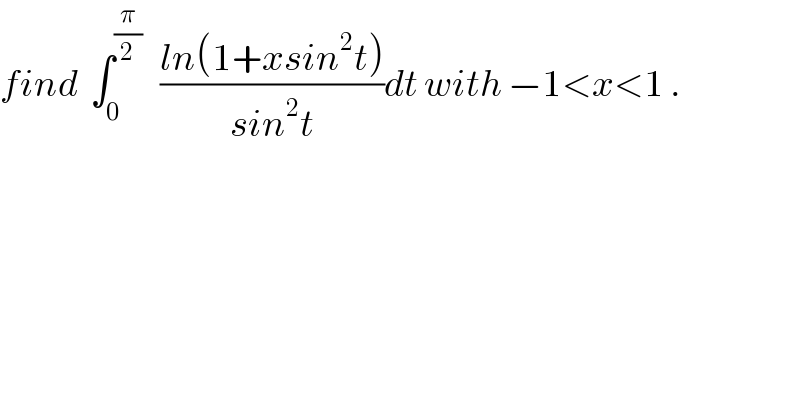 | ||
Commented by abdo imad last updated on 09/Jan/18 | ||
![let put f(x)= ∫_0 ^(π/2) ((ln(1+xsin^2 t))/(sin^2 t))dt after verifying that f is derivable on ]−1,1[ we have f^, (x)= ∫_0 ^(π/2) (dt/(1+xsin^2 t)) because of /xsin^2 t/<1 f^′ (x)= ∫_0 ^(π/2) ( Σ_(n=0) ^∝ (−1)^n x^n sin^(2n) t)dt =Σ_(n=0) ^∝ (−1)^n x^n ∫_0 ^(π/2) sin^(2n) tdt= Σ_(n=0) ^∝ (−1)^n W_n x^n with W_n = ∫_0 ^(π/2) sin^(2n) tdt and the value of W_n is known (walliss integral) f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n x^(n+1) +λ λ=f(0)=0⇒ f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n .x^(n+1) .](Q27573.png) | ||