Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 35058 by math khazana by abdo last updated on 14/May/18

$$find{\int }_0^{\frac{\pi }{4}}\frac{dt}{{(1+{cos}^{2}t)}^3}$$

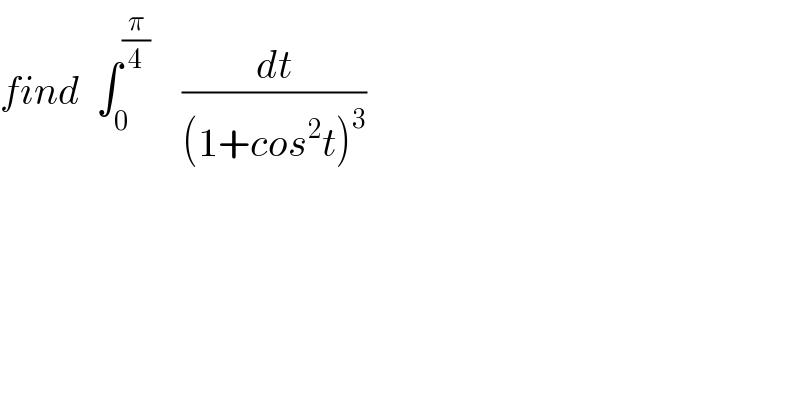
Commented by abdo mathsup 649 cc last updated on 18/May/18

$$letputI={\int }_0^{\frac{\pi }{4}}\frac{dt}{{(1+{cos}^{2}t)}^3}$$$$I={\int }_0^{\frac{\pi }{4}}\frac{dt}{{(1+\frac{1+cos\left(2t\right)}{2})}^3}$$$$=8{\int }_0^{\frac{\pi }{4}}\frac{dt}{{(3+cos\left(2t\right))}^3}{=}_{2t=x}8{\int }_0^{\frac{\pi }{2}}\frac{1}{{(3+cosx)}^3}\frac{dx}{2}$$$$=4{\int }_0^{\frac{\pi }{2}}\frac{dx}{{(3+cosx)}^3}.changementtan\left(\frac{x}{2}\right)=t$$$$giveI=4{\int }_0^1\frac{1}{{(3+\frac{1-t^2}{1+t^2})}^3}\frac{2dt}{1+t^2}$$$$I=8{\int }_0^1\frac{{(1+t^2)}^2}{{(3+3t^2+1-t^2)}^3}dt$$$$I=8{\int }_0^1\frac{{(1+t^2)}^2}{{(4+2t^2)}^3}dt={\int }_0^1\frac{{(1+t^2)}^2}{{(2+t^2)}^3}dt$$$$I={\int }_0^1\frac{t^4+2t^2+1}{8+3.2^2{t}^2+3.2.t^4+t^6}dt$$$$={\int }_0^1\frac{t^4+2t^2+1}{t^6+6t^4+12t^2+8}dtletdecompose$$$$F\left(t\right)=\frac{t^4+2t^2+1}{t^6+6t^4+12t^2+8}.....becontinued...$$

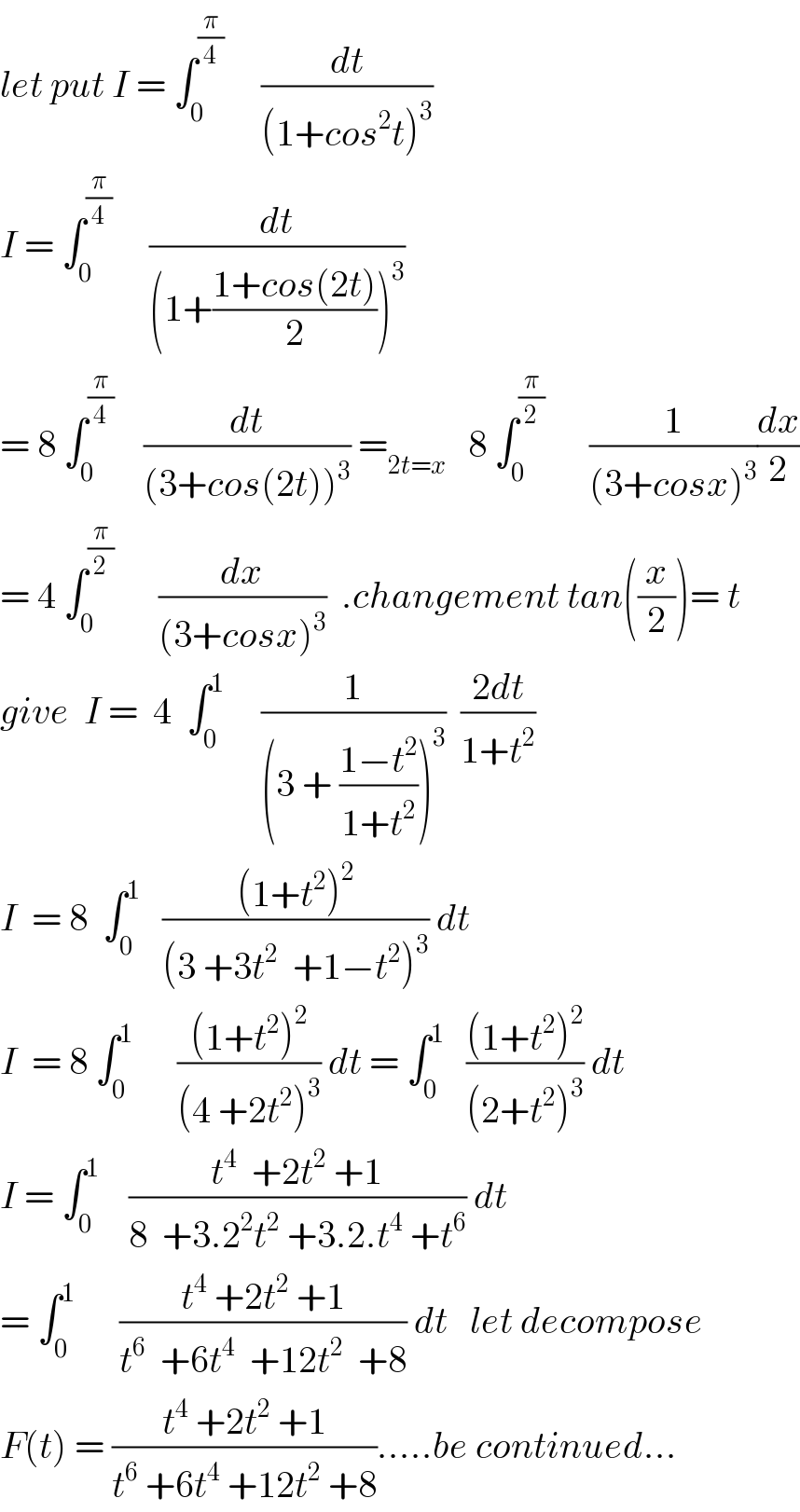
Answered by MJS last updated on 16/May/18

$$\int \frac{dt}{{(1+{\cos }^2\left(t\right))}^3}=$$$$[\cos \left(t\right)=\frac{1}{\sec \left(t\right)};{\sec }^2\left(t\right)={\tan }^2\left(t\right)+1]$$$$=\int \frac{{\sec }^2\left(t\right){({\tan }^2\left(t\right)+1)}^2}{{({\tan }^2\left(t\right)+2)}^3}dt=$$$$[u=\tan \left(t\right)\to dt=\frac{du}{{\sec }^2\left(t\right)}]$$$$=\int \frac{{(u^2+1)}^2}{{(u^2+2)}^3}du=\int \frac{du}{u^2+2}-2\int \frac{du}{{(u^2+2)}^2}+\int \frac{du}{{(u^2+2)}^3}=$$$$$$$$\int \frac{du}{u^2+2}=$$$$[v=\frac{\sqrt{2}}{2}u\to du=dv\sqrt{2}]$$$$=\frac{\sqrt{2}}{2}\int \frac{dv}{v^2+1}=\frac{\sqrt{2}}{2}\arctan \left(v\right)=\frac{\sqrt{2}}{2}\arctan \left(\frac{\sqrt{2}}{2}u\right)$$$$$$$$-2\int \frac{du}{{(u^2+2)}^2}=$$$$[\int \frac{du}{{({au}^2+b)}^n}=\frac{u}{2b(n-1){({au}^2+b)}^{n-1}}+\frac{2n-3}{2b(n-1)}\int \frac{du}{{({au}^2+b)}^{n-1}}]$$$$=-2(\frac{u}{4(u^2+2)}+\frac{1}{4}\int \frac{du}{u^2+2})=$$$$=-\frac{u}{2(u^2+2)}-\frac{\sqrt{2}}{4}\arctan \left(\frac{\sqrt{2}}{2}u\right)$$$$$$$$\int \frac{du}{{(u^2+2)}^3}=\frac{u}{8{(u^2+2)}^2}+\frac{3}{8}\int \frac{du}{{(u^2+2)}^2}=$$$$=\frac{u}{8{(u^2+2)}^2}+\frac{3}{8}(\frac{u}{4(u^2+2)}+\frac{\sqrt{2}}{8}\arctan \left(\frac{\sqrt{2}}{2}u\right))=$$$$=\frac{u}{8{(u^2+2)}^2}+\frac{3u}{32(u^2+2)}+\frac{3\sqrt{2}}{64}\arctan \left(\frac{\sqrt{2}}{2}u\right)$$$$$$$$=\frac{19\sqrt{2}}{64}\arctan \left(\frac{\sqrt{2}}{2}u\right)-\frac{13u}{32(u^2+2)}+\frac{u}{8{(u^2+2)}^2}=$$$$=\frac{19\sqrt{2}}{64}\arctan \left(\frac{\sqrt{2}}{2}\tan \left(t\right)\right)-\frac{\tan \left(t\right)({13\tan }^2\left(t\right)+22)}{32{({\tan }^2\left(t\right)+2)}^2}+C$$$$$$$$\underset{0}{\stackrel{\frac{\pi }{4}}{\int }}\frac{dt}{{(1+{\cos }^2\left(t\right))}^3}=\frac{19\sqrt{2}}{64}\arctan \left(\frac{\sqrt{2}}{2}\right)-\frac{35}{288}$$

Commented by abdo mathsup 649 cc last updated on 15/May/18

$$thankyousirMjsforthishardwork...$$

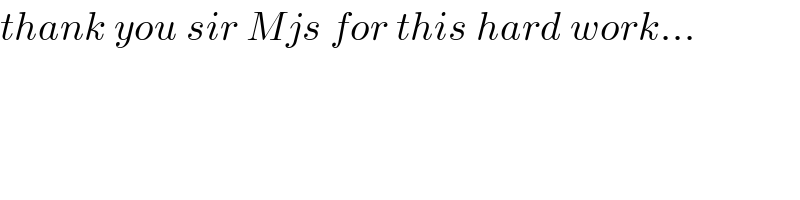
Commented by MJS last updated on 16/May/18

$${\mathrm{you}}^{\prime }\mathrm{re}\mathrm{welcome},\mathrm{it}\mathrm{keeps}\mathrm{my}\mathrm{brains}\mathrm{young}$$

Commented by abdo mathsup 649 cc last updated on 16/May/18

$$areyouadoctororenjenersirMjs...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com