
Question and Answers Forum
Question Number 35054 by math khazana by abdo last updated on 14/May/18
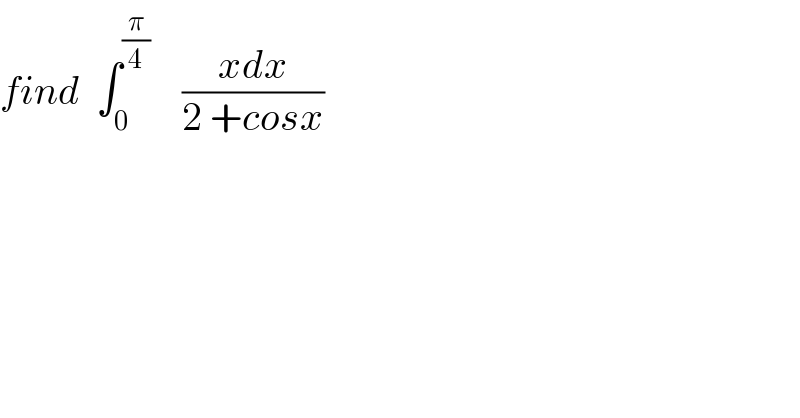
Commented by prof Abdo imad last updated on 16/May/18
![changement tan((x/2))=t give I = ∫_0 ^((√2) −1) ((2arctant)/(2+ ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = 4 ∫_0 ^((√2) −1) ((arctant)/(2 +2t^2 +1−t^2 ))dt =4 ∫_0 ^((√2) −1) ((arctan(t))/(3+t^2 )) dt =_(t=(√3)u) 4 ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(3(1+u^2 ))) (√3) du =((4(√3))/3) ∫_0 ^(((√2) −1)/3) ((arctan((√3)u))/(1+u^2 ))du by parts ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(1+u^2 ))du = [arctan(u)arctan((√3)u)]_0 ^(((√2)−1)/3) −(√3)∫_0 ^(((√2) −1)/3) ((arctan(u))/(1+3u^2 ))du =arctan((((√2) −1)/3))arctan((√3)(((√2) −1)/3)) −(√3) ∫_0 ^(((√2)−1)/3) ((arctan(u))/(1+3u^2 )) du....be continued...](Q35185.png)
| ||
Question and Answers Forum | ||
Question Number 35054 by math khazana by abdo last updated on 14/May/18 | ||
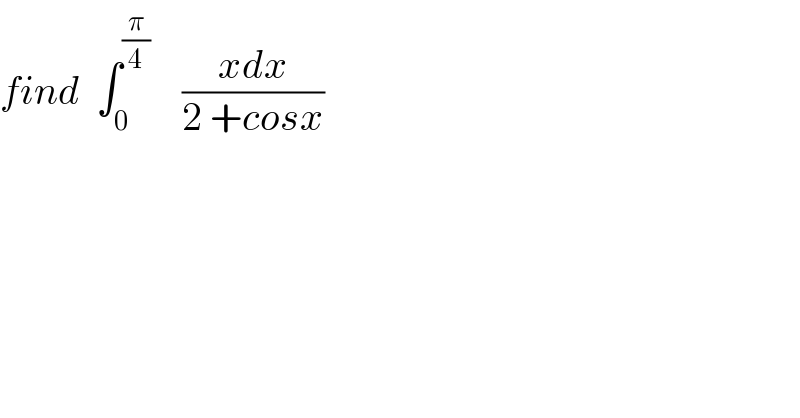 | ||
Commented by prof Abdo imad last updated on 16/May/18 | ||
![changement tan((x/2))=t give I = ∫_0 ^((√2) −1) ((2arctant)/(2+ ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = 4 ∫_0 ^((√2) −1) ((arctant)/(2 +2t^2 +1−t^2 ))dt =4 ∫_0 ^((√2) −1) ((arctan(t))/(3+t^2 )) dt =_(t=(√3)u) 4 ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(3(1+u^2 ))) (√3) du =((4(√3))/3) ∫_0 ^(((√2) −1)/3) ((arctan((√3)u))/(1+u^2 ))du by parts ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(1+u^2 ))du = [arctan(u)arctan((√3)u)]_0 ^(((√2)−1)/3) −(√3)∫_0 ^(((√2) −1)/3) ((arctan(u))/(1+3u^2 ))du =arctan((((√2) −1)/3))arctan((√3)(((√2) −1)/3)) −(√3) ∫_0 ^(((√2)−1)/3) ((arctan(u))/(1+3u^2 )) du....be continued...](Q35185.png) | ||