Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 31071 by abdo imad last updated on 02/Mar/18

$$find{\int }_0^{\pi }\frac{dx}{1+{sin}^{2}x}.$$

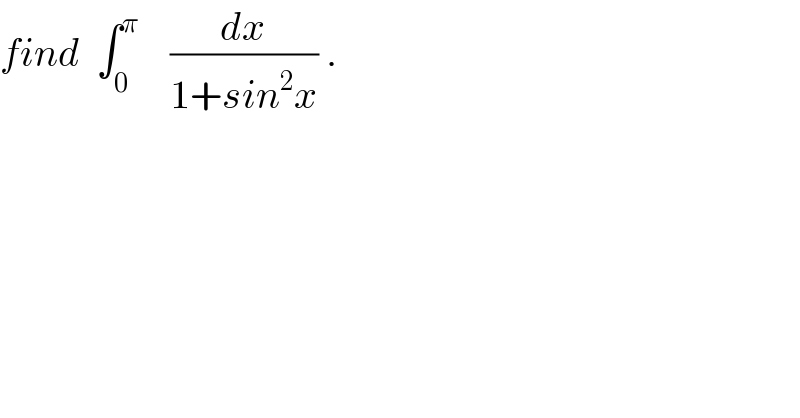
Commented by abdo imad last updated on 03/Mar/18

$$thanks.$$

Commented by abdo imad last updated on 02/Mar/18

$$letputI={\int }_0^{\pi }\frac{dx}{1+{sin}^{2}x}\Rightarrow I={\int }_0^{\pi }\frac{dx}{1+\frac{1-cos\left(2x\right)}{2}}$$$$={\int }_0^{\pi }\frac{2dx}{3-cos\left(2x\right)}{=}_{t=2x}{\int }_0^{2\pi }\frac{dt}{3-cost}thech.e^{it}=zgive$$$$I={\int }_{\mid z\mid =1}\frac{1}{3-\frac{z+z^{-1}}{2}}\frac{dz}{iz}={\int }_{\mid z\mid =1}\frac{2dz}{iz(6-(z+z^{-1}))}$$$$={\int }_{\mid z\mid =1}\frac{-2idz}{6z-z^2-1}={\int }_{\mid z\mid =1}\frac{2idz}{z^2-6z+1}letput$$$$\phi \left(z\right)=\frac{2i}{z^2-6z+1}.polesof\phi ?$$$$z^2-6z+1=0\Rightarrow {\mathrm{\Delta }}^{{}^{\prime }}={(-3)}^2-1=8\Rightarrow z_1=3+2\sqrt{2}$$$$z_2=3-2\sqrt{2}\mid z_1\mid -1=3+2\sqrt{2}-1=2+2\sqrt{2}>0(toeliminate$$$$fromresidus)\mid z_2\mid -1=2-2\sqrt{2}=2(1-\sqrt{2)}<0\Rightarrow$$$${\int }_{\mid z\mid =1}\phi \left(z\right)dz=2i\pi Res(\phi ,z_2)but$$$$\phi \left(z\right)=\frac{2i}{(z-z_1)(z-z_2)}\Rightarrow Res(\phi ,z_2)=\frac{2i}{z_2-z_1}=\frac{2i}{-4\sqrt{2}}=\frac{-i}{2\sqrt{2}}$$$${\int }_{\mid z\mid =1}\phi \left(z\right)dz=2i\pi .\frac{-i}{2\sqrt{2}}=\frac{\pi }{\sqrt{2}}\Rightarrow I=\frac{\pi }{\sqrt{2}}.$$$$$$$$$$

Commented by Joel578 last updated on 02/Mar/18

$$\mathrm{Nice}\mathrm{solution},\mathrm{Sir}$$

Answered by Joel578 last updated on 02/Mar/18

$$I={\int }_0^{\pi }\frac{{\mathrm{cosec}}^{2}x}{(1+{\sin }^{2}x){\mathrm{cosec}}^{2}x}dx$$$$={\int }_0^{\pi }\frac{{\mathrm{cosec}}^{2}x}{{\mathrm{cosec}}^{2}x+1}dx$$$$={\int }_0^{\pi }\frac{{\mathrm{cosec}}^{2}x}{{\cot }^{2}x+2}dx$$$$$$$$u=\cot x\to du=-{\mathrm{cosec}}^{2}xdx$$$$=-\int \frac{{\mathrm{cosec}}^{2}x}{u^2+2}.\frac{du}{{\mathrm{cosec}}^{2}x}=-\int \frac{du}{u^2+2}$$$$$$$$u=\sqrt{2}\tan \theta \to du=\sqrt{2}{\sec }^2\theta d\theta$$$$I=-\sqrt{2}\int \frac{{\sec }^2\theta }{2({\tan }^2\theta +1)}d\theta$$$$=-\frac{\sqrt{2}}{2}\int d\theta$$$$=-\frac{\sqrt{2}}{2}\theta +C=-\frac{\sqrt{2}}{2}{\tan }^{-1}\left(\frac{u}{\sqrt{2}}\right)+C$$$$=-\frac{\sqrt{2}}{2}{\tan }^{-1}\left(\frac{\cot x}{\sqrt{2}}\right)+C$$$$$$$$I={[-\frac{\sqrt{2}}{2}{\tan }^{-1}\left(\frac{\cot x}{\sqrt{2}}\right)]}_0^{\pi }$$$$=(-\frac{\sqrt{2}}{2}{\tan }^{-1}(-\mathrm{\infty }))-(-\frac{\sqrt{2}}{2}{\tan }^{-1}\left(\mathrm{\infty }\right))$$$$=\frac{\pi \sqrt{2}}{4}+\frac{\pi \sqrt{2}}{4}=\frac{\pi \sqrt{2}}{2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com